Enotne pravokotne značilnosti gibanja, formule, vaje

On Enotno gibanje linij ali s konstantno hitrostjo je tisti, v katerem se delček premika po ravni črti in s konstantno hitrostjo. Na ta način mobilni telefon potuje v enakih razdaljah v enakih časih. Na primer, če v 1 sekundi potuje 2 metra, po 2 sekundah bo 4 metra in tako naprej.

Za natančen opis gibanja, bodisi enakomernega pravokotnega ali katerega koli drugega, je treba vzpostaviti referenčno točko, imenovano tudi izvor, Glede na to, v kateri mobilni spreminjajo pozicijo.

Slika 1. Avtomobil, ki se premika po pravokotni cesti s konstantno hitrostjo, ima enakomerno pravokotno gibanje. Vir: Pixabay.

Če gibanje poteka v celoti vzdolž ravne črte, ga zanima tudi vedeti, v kakšnem smislu potuje.

Na vodoravni črti je možno, da mobilni telefon gre v desno ali na levo. Razlikovanje med obema situacijama je z znaki, naslednje pa je naslednje: desno sledim (+) in na levi znak (--).

Ko je hitrost konstantna, mobilni telefon ne spremeni svoje smeri ali pomena in tudi velikost njegove hitrosti ostane nespremenjena.

[TOC]

Značilnosti

Glavne značilnosti enotnega pravokotnega gibanja (MRU) so naslednje:

-Gibanje vedno prehaja po ravni črti.

-Mobilec z MRU v enakih časih potuje z enakimi razdaljami ali prostori.

-Hitrost ostane nesprejemljiva tako po velikosti kot smeri.

-MRU primanjkuje pospeška (ni sprememb hitrosti).

-Od hitrosti v ostaja konstanten sčasoma t, Graf njene velikosti kot funkcije časa je ravna črta. Na primeru slike 2 je črta zelena in vrednost hitrosti se bere na navpični osi, približno +0.68 m/s.

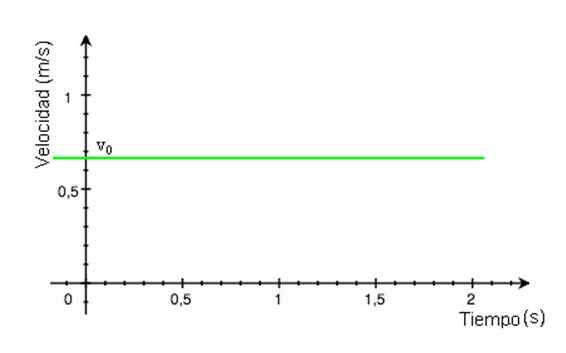Slika 2. Hitrostni graf, odvisno od MRU. Vir: Wikimedia Commons.

-Graf položaja X glede na čas je ravna črta, katere naklon je enakovreden mobilni hitrosti. Če je črta grafa x vs t vodoravna, je mobilni telefon v mirovanju, če je naklon pozitiven (graf slike 3), je tudi hitrost.

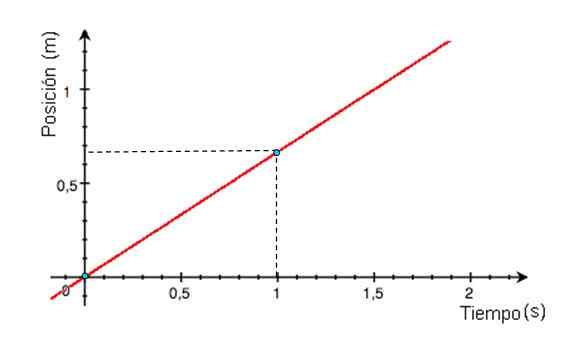Slika 3. Graf položaja kot funkcija časa za mobilni telefon z MRU, ki se je oddaljil od izvora. Vir: Wikimedia Commons.

Razdalja, prevožena od grafa V proti. t

Spoznajte razdaljo, ki jo prevozi mobilni telefon, ko je graf na voljo v Vs. T je zelo preprost. Prevožena razdalja je enakovredna območju pod črto in je vključena v želeni časovni interval.

Lahko vam služi: povprečni pospešek: kako se izračuna in reši

Recimo, da želite vedeti razdaljo, ki jo prevozi mobilni telefon slike 2 v intervalu med 0.5 in 1.5 sekund.

To območje je za senčen pravokotnik na sliki 4. Izračuna se tako, da najdemo rezultat pomnožitve osnove pravokotnika po njegovi višini, katere vrednosti se berejo iz grafike.

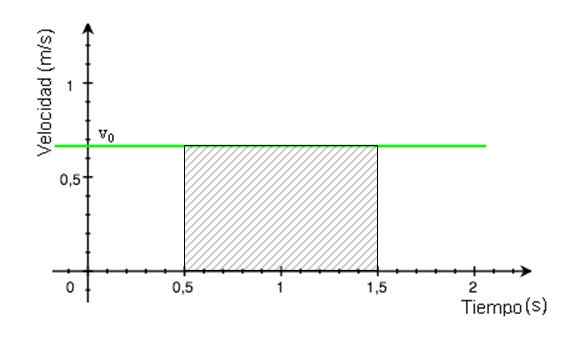Slika 4. Striped območje je enakovredno prevoženi razdalji. Vir: Modified Wikimedia Commons.

Prevožena razdalja = (1.petdeset.5) x 0.68 m = 0.68 m

Razdalja je vedno pozitiven znesek, ne glede na to, ali greš v desno ali na levo.

Formule in enačbe

V MRU sta povprečna hitrost in trenutna hitrost vedno enaka, in ker je njegova vrednost naklon grafa x vs t, ki ustreza črti, so ustrezne enačbe, odvisno od časa, naslednje:

-Položaj, odvisno od časa: x (t) = x_tudi + Vt

x_tudi Predstavlja začetni položaj mobilnega telefona, večkrat pa sovpada z izvorom referenčnega sistema, vendar ni vedno tako. Ta enačba je znana tudi kot Enačba poti.

-Hitrost, odvisno od časa: v (t) = konstanta

Ko v = 0 pomeni, da je mobilni telefon počitek. Počitek je poseben primer gibanja.

-Pospešek kot funkcija časa: A (t) = 0

V enotnem pravokotnem gibanju ni sprememb hitrosti, zato je pospešek nič.

Rešene vaje

V času reševanja vaje je treba zagotoviti, da situacija ustreza modelu, ki ga je treba uporabiti. Pred uporabo enačb MRU je treba zagotoviti, da so uporabne.

Naslednje rešene vaje sta dve mobilni težavi.

Vaja rešena 1

Dva športnika se med seboj približata s stalno hitrostjo 4.50 m/s in 3.5 m/s, ki je bil prvotno ločen na razdalji 100 metrov, kot je navedeno na sliki.

Če vsak ohrani svojo konstantno hitrost, poiščite: a) kako dolgo traja srečanje? b) Kakšen bo položaj vsakega takrat?

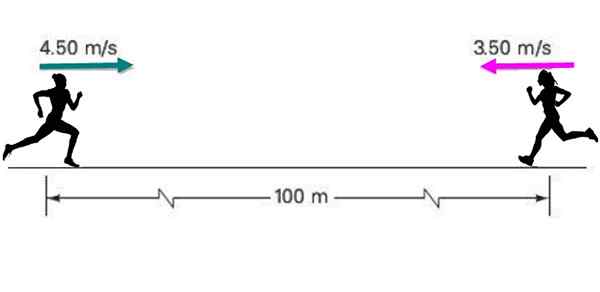Slika 5. Dva tekača se premikata drug v drugega. Vir: Self Made.

Rešitev

Prva je, da označi izvor koordinatnega sistema, ki bo služil kot referenca. Izbira je odvisna od naklonjenosti, ki jo ima oseba, ki reši težavo.

Vam lahko služi: kaj je volumetrična dilatacija? (S primeri)

Običajno je izbran x = 0 desno na izhodišču mobilnih telefonov, lahko je v tekač leve ali desne, izbrati ga je mogoče celo na sredini obeh.

a) Izbrali bomo x = 0 na tekaču leve ali tekača 1, zato je začetni položaj tega x₀₁ = 0 in za Runner 2 bo x₀₂ = 100 m. Posrednik 1 se premika od leve proti desni s hitrostjo V₁ = 4.50 m/ medtem ko tekač 2 to počne od desne proti levi s hitrostjo -3.50 m/s.

Enačba gibanja za prvega posrednika

x₁ = x₀₁ + v₁t₁ = 4.50t₁

Enačba gibanja za drugega posrednika

x₂ = x₀₂ + v₂t₂ = 100 -3.50t₂

Ker je čas enak za oba t₁ = t₂ = t , Ko bo položaj obeh, bo torej enak x₁ = x₂. Enako:

4.50t = 100 -3.50t

To je enačba prve stopnje za čas, katere rešitev je t = 12.5 s.

b) Oba tekača sta v istem položaju, zato nadomešča čas, pridobljen v prejšnjem razdelku v katerem koli od enačb položaja. Na primer, lahko uporabimo Runner 1:

x₁ = 4.50t₁ = 56.25 m

Isti rezultat dobimo z zamenjavo t = 12.5 s v enačbi položaja tekačev 2.

-Vaja Rešena 2

Hare izziva želvo, da teče razdaljo 2.4 km in pošteno ponuja pol ure prednosti. V igri želva napreduje z razlogom 0.25 m/s, kar je največ, kar lahko zažene. Po 30 minutah zajček teče pri 2 m/s in hitro doseže želvo.

Potem ko nadaljuje še 15 minut, pomislite, da ima čas, da se zaspi in še vedno zmaga na dirki, vendar zaspi 111 minut. Ko se zbudi, teče z vso svojo močjo, a želva je že prečkala cilj. Najti:

a) kakšna prednost ima želva?

b) trenutek časa, v katerem zajček napreduje želvo

c) trenutek, ko želva napreduje.

Rešitev)

Dirka se začne v t = 0. Položaj želve: x_T = 0.25T

Gibanje zajca ima naslednje dele:

Vam lahko služi: sončni sistem: planeti, značilnosti, izvor, evolucija

-Počivaj za prednost, ki jo je dal želvi: 0 < t < 30 minutos:

-Dirka, da pridete do želve in nadaljujte z malo, potem ko jo prehodite; Skupaj so 15 minut gibanja.

-Spite 111 minut (počitek)

-Zbudi se prepozno (sprint finale)

2.4 km = 2400 m

Trajanje dirke je bilo: T = 2400 m/ 0.25 m/s = 9600 s = 160 min. V tem času odštejemo 111 minut od na NAP in 30, kar je 19 minut (1140 sekund). To pomeni, da je tekel 15 minut pred spanjem in 4 minute po prebujanju za sprint.

V tem času je zajček prevozil naslednjo razdaljo:

d_L = 2 m/s . (petnajst . 60 s) + 2 m/s (4. 60 s) = 1800 m + 480 m = 2280 m.

Ker je bila skupna razdalja 2400 metrov, odšteva se obe vrednosti, se izkaže, da je zajček manjkalo 120 metrov, da bi dosegel cilj.

Rešitev B)

Položaj zajca pred zaspanjem je x_L = 2 (T - 1800), Glede na 30 -milijonsko zamudo = 1800 sekund. Enako x_T in x_L Najdemo čas, ko so:

2 (T - 1800) = 0.25T

2T -0.25 t = 3600

T = 2057.14 S = 34.29 min

Rešitev C)

Do trenutka, ko je Hare napredoval želva, to spi na 1800 metrih od igre:

1800 = 0.25T

T = 7200 s = 120 min

Prijave

MRU je najpreprostejše gibanje, ki si ga je mogoče zamisliti in zato je prvi, ki ga je treba preučiti v kinematografiji, vendar je mogoče veliko zapletenih gibov opisati kot kombinacijo tega in drugih preprostih gibov.

Če človek zapusti svojo hišo in vodi, dokler ne doseže dolge pravokotne avtoceste, skozi katero dlje časa potuje do enake hitrosti, je mogoče opisati njegovo gibanje kot MRU, ne da bi se lotil več podrobnosti.

Seveda mora oseba pred vstopom in zapuščanjem avtoceste vzeti nekaj krogov, vendar lahko z uporabo tega modela gibanja ocenimo trajanje potovanja, ki pozna približno razdaljo med izhodiščno točko in točko prihoda.

V naravi ima svetloba enotno pravokotno gibanje, katerega hitrost je 300.000 km/s. Tudi gibanje zvoka v zraku lahko predvidevamo enakomerno rektomino s hitrostjo 340 m/s v številnih aplikacijah.

Pri analizi drugih težav, na primer gibanje nosilcev obremenitve znotraj prevodne žice, lahko pristop MRU uporabimo tudi za predstavo o tem, kaj se zgodi znotraj voznika.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.40-45.
2. Figueroa, d. Fizične serije za znanost in inženiring. Zvezek 3. Izdaja. Kinematika. 69-85.
3. Giancoli, d.  Fizika: načela z aplikacijami. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Konceptualna fizikalna znanost. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, l. 2007. Fizika: pogled na svet. 6^ta Skrajšana izdaja. Cengage učenje. 15-19.
6. Wilson, J. 2011. Fizika 10. Pearson Education. 116-119.