Enotno krožno gibanje (m.C.Ali.) formule, značilnosti

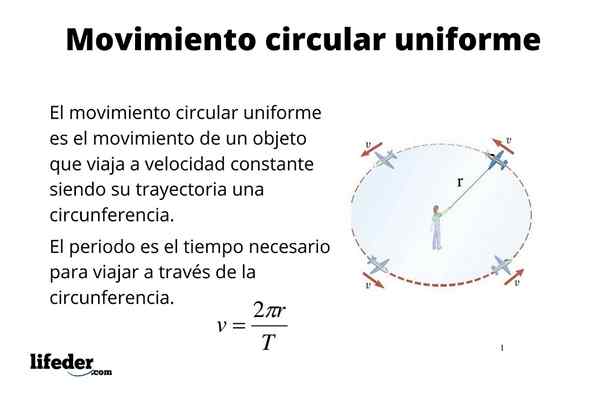
Delček ima krožno gibanje enotna (M.C.Ali.) Ko je njegova pot obod in jo tudi nenehno potuje. Številni predmeti, kot so na primer koščki strojev in motorjev, imajo tovrstno gibanje, med katerimi so trdi diski računalnikov, fenater, seki.

Enotno krožno gibanje je tudi dober pristop k gibanju nekaterih nebesnih teles, kot je Zemlja. Zemljina orbita je res eliptična, kot poudarjajo Keplerjevi zakoni. Vendar je ekscentričnost orbite majhna in kot prvi pristop se lahko šteje za krožno, kar poenostavlja nekatere izračune, na primer iskanje hitrosti zemlje, ko se premika okoli sonca.

V opisu enotnega krožnega gibanja se uporabljajo isti parametri kot v pravokotnem gibanju, in sicer: položaj, premik, čas, hitrost in pospeševanje.

Pospešek? Da, dejansko se pospeši enotno krožno gibanje, tudi ko je njegova hitrost v biti konstanten. To je zato, ker hitrost v, Da je vektor in zato je krepko, nenehno spreminja svojo smer, ko se objekt ali delček vrti. Kakršna koli sprememba v Nastaja s pospeševanjem, ki je, kot bo razvidno, usmerjeno proti središču krožne poti.

Enotno krožno gibanje je gibanje v ravnini Xy, Zato gre za dvodimenzionalno gibanje. Vendar ga je mogoče bolj udobno izraziti skozi kot θ, ki pometa delček, merjeno glede na vodoravno osi ali drugo ustrezno referenčno osi.

Tudi če gre za razširjen predmet, njegovi delci vedno pometajo enak kot, tudi če imajo različne koordinate (X, y).

[TOC]

Značilnosti enotnega krožnega gibanja

Značilnosti enotnega krožnega gibanja lahko povzamete na naslednji način:

-Usmeritev je obod, zato je gibanje v ravnini.

-Hitrost v Je konstantna, a hitrost v Ne, ker nenehno spreminja smer in pomen, da prilagodi zavoj mobilnega telefona.

-Vektor hitrosti v Vedno je tangencialno za obod in pravokotno na radialno smer.

-Kotna hitrost ω je konstantna.

-Kljub temu, da ste enotni, obstaja pospeševanje, ki razloži te spremembe v smeri hitrosti. Ta pospešek je centripetalni pospešek.

-Centripetalni pospešek in hitrost sta med seboj pravokotna.

-Gre za periodično ali ponavljajoče se gibanje, zato sta zanj določena obdobje in pogostost.

Enotne formule krožnega gibanja

V tej shemi je zavrtitev delcev v narisano.

Vam lahko služi: Zemljino magnetno polje: izvor, značilnosti, funkcija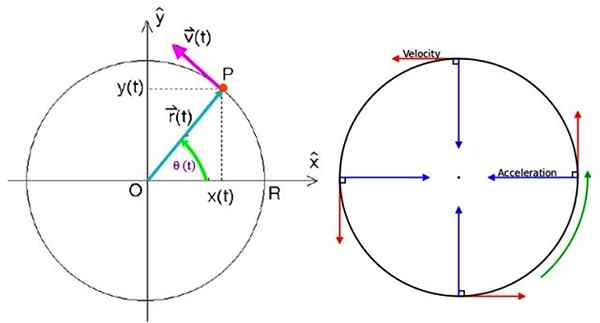 Enotni krožni parametri gibanja. Vir: f. Zapata/Wikimedia Commons.

Za določitev položaja vektorja je potrebno.

Položaj vektor

Označen je kot r (t) in je usmerjen od izvora do točke P, kjer se nahaja delček. V trenutku, ko je t, v kartezijanskih koordinatah, je napisano kot:

r (t) = x (t) Yo + in (t) J

Kje Yo in J So vektorji pravokotnih enot v smeri x in in oziroma. Grafa je opaziti, da vektorski modul r (t) Vedno v redu R, Polmer oboda. Če je θ kot, ki tvori r Z vodoravno osi je tudi položaj enak:

r (t) = [RCOS θ(t)] Yo +[RSEN θ(t)] J

Kot, ki tvori r (T) Z vodoravno osi je osrednji kot in njegova vrednost je:

θ = s/r

Kjer je S prehoden lok in r radio. Je rekel kot θ To je časovna funkcija, tako da lahko pišete θ = θ (T), KLIČITE kotni položaj.

Ker je hitrost konstantna, delček opisuje enake kote v enakih časih in v analogiji z enakomernim pravokotnim gibanjem, je napisan:

θ = θ (t) = θ_tudi + ωt

Tukaj θ_tudi To je začetni kot, izmerjen v radianih glede na referenčno osi, lahko je 0 ali poljubna vrednost, ω pa kotna hitrost.

Kotna hitrost in linearna hitrost

Kotna hitrost je prva izhaja iz kotnega položaja in je označena kot ω. Njegova vrednost je konstantna za enakomerno krožno gibanje, saj se enaki koti v enakih časih ograjajo. Z drugimi besedami:

Kotna hitrost je v enotah radianov. Linearna hitrost se izračuna z::

Linearna hitrost je modul ali jakost linearne hitrosti, ki se spreminja, ko se delček ob njegovi poti obrne. Smer hitrosti je torej tangencialni naslov do oboda.

Enote linearne hitrosti v enakomernem krožnem gibanju so enake kot pri linearnih gibih: m/s (v mednarodnem sistemu SI), km/h, cm/s in druge.

Centripetalni pospešek

Na naslednji sliki je delček, ki se premika v razporedu oboda s konstantno hitrostjo. To pomeni, da ima vektor hitrosti vedno enak modul, vendar spreminja smer, da se prilagodi obodu.

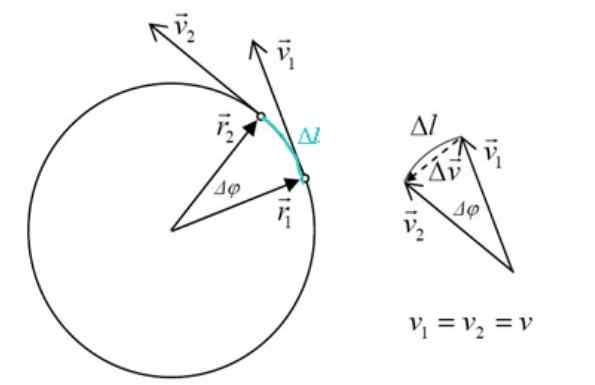Hitrost in pospešek v enotnem krožnem gibanju. Vir: f. Zapata.

Vsaka sprememba hitrosti rezultatov na pospešek, kar je po definiciji:

Vam lahko služi: 31 vrst sile v fiziki in njihove značilnosti

Na zgornji sliki je odštevanje med vektorji v₂ in v₁, čigar rezultat je δv, vektorsko sorazmerno s pospeševanjem. Kot vidite, vedno kaže na središče oboda in zato se imenuje centripetalni pospešek ali radialni pospešek.

Trikotnik, ki ga tvori v₂, v₁ in δv Podobno je s strani Trikotnika r₂, r₁ in δl, Biti Δφ osrednji kot. Veličine r₂ in r₁ So enaki, torej:

r₂ = r₁ = r

Potem so obeh trikotnikov ta odnos za kot:

Δφ = Δr / r; Δφ = ΔV / V

Krepke niso potrebne, saj je merilo kota odvisno od velikosti teh vektorjev. Izenačenje zgornjih izrazov sledi:

 Tako:

Delitev na obeh straneh z ΔT, da dobimo velikost pospeška:

Toda ΔR / ΔT je velikost hitrosti, imenovana v, Zato:

Končno je pospeševanje centripetala:

Obdobje in frekvenca

Ker se krožno gibanje ponavlja, je obdobje definirano T enako kot čas, ki ga potrebuje za mobilni telefon. Ker je dolžina polmera polmera r 2πr, je kot, ki je pri obračanju popolnega prelistala, 2π radianov in traja čas t, kotna hitrost je:

Ω = 2π / t

T = 2π / Ω

Obdobje enotnega krožnega gibanja se meri v nekaj sekundah v mednarodnem sistemu.

S svojo stranjo F To je število zavojev na enoto časa in je vzajemno ali obratno v obdobju:

F = n /t = 1 /t

Frekvenčna enota v mednarodnem sistemu je s^-1.

Primeri enotnega krožnega gibanja

Številni predmeti se vrtijo, da ustvarijo različne učinke: kolesa, diski in turbine. Ko dosežemo obratovalno hitrost, se vrtenje običajno izvaja s konstantno hitrostjo. Krožno gibanje je tako pogosto v vsakdanjem življenju, da o tem skoraj nikoli ne razmišljate, zato je tu nekaj tesnih primerov, ki zelo dobro ponazarjajo:

Zemljino gibanje

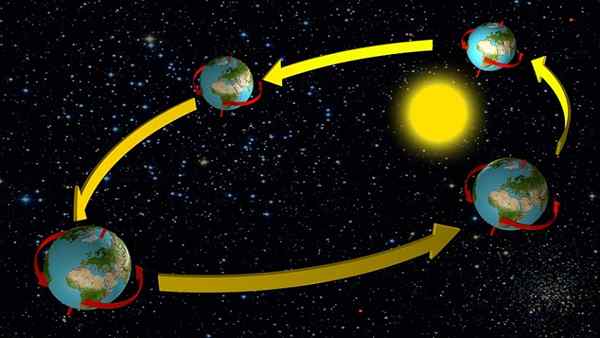
Zemlja in drugi planeti sončnega sistema se premikajo v eliptičnih usmeritvah majhne ekscentričnosti, razen živega srebra, kar pomeni, da je v prvem pristopu mogoče domnevati, da je njegovo gibanje enakomerno krožno.

To ima dobro predstavo o hitrosti prevajanja okoli sonca, saj je v primeru Zemlje znano obdobje gibanja: eno leto ali 365 dni.

Delci na robu albuma

Delci, ki se vrtijo na robu starodavnih toadiscosov ali modela ventilatorja, sledijo enakomernemu krožnemu gibanju, ko naprava doseže hitrost razmnoževanja.

Vam lahko služi: Dirac Jordan Atomski model: značilnosti in postulati

Hubble vesoljski teleskop

Hubble vesoljski teleskop se vrti okoli zemlje pri približno 7550 m/s.

Centrifugatorji

Pralni stroji izvajajo centrifugiran postopek za stiskanje oblačil, ki je sestavljen iz vrtenja bobna za kontejner. Tudi sušilniki se za nekaj časa obrnejo z enakomernim krožnim gibanjem.

Centrifugiranje se na primer uporablja tudi v laboratorijih za ločevanje spojin in tako loči njene sestavine glede na razliko v gostoti. Kadar koli se govori o centrifugiranju, obstaja krožno gibanje, ki je enotno, vsaj za nekaj časa.

Vrtni tuši

Številni vrtni tuši nenehno obračajo, da bi zemlja v paru zalivala.

Šport

Na primer v izstrelitvi kladiva, ki je olimpijska disciplina, športnik obrne kovinsko kroglico z jeklenim kablom, pritrjenim na ročaj. Cilj je poslati žogo, kolikor je mogoče, vendar ne da bi zapustili določeno območje.

Vaja rešena

Delec se premika v krogu polmera 2m s konstantno hitrostjo v = 8 m/s, v nasprotni smeri do ure. Sprva je bil delček v r = +2 J m. Izračunati:

a) Kotna hitrost Ω

b) njen kotni položaj θ (t)

c) obdobje gibanja

d) pospeševanje centripetalnega.

e) Položaj delca po prehodu t = π/4 s

Rešitev

Iz formule V = rΩ sledi, da:

Ω = v/r = (8 m/s)/2m = 4rad ∙ s^-1

Rešitev b

Kot referenčna os na pozitivno osi X je delček sprva pri 90 ° = π/2 radians glede na omenjeno osi, saj v izjavi piše, da je začetni položaj +2 J m, torej delček je v y = 2m, ko začne gibanje slediti.

θ = θ (t) = θ_tudi + ωt = π/2 + 4t

Rešitev c

T = 2π / ω = 2π / 4 s = 0.5 π s

Rešitev d

a = v² / R = (8 m/ s)² / 2 m = 32 m/ s²

Rešitev e

θ (t) = π/2 + 4T → θ (π/4) = π/2 + 4 ∙ (π/4) = 3π/2 radians

To pomeni, da je po tem času delček v položaju y = -2m J. Smiselno je, ker je t = π/4 s polovica obdobja, zato je delček od svojega začetnega položaja obiskal kot 180 ° v protirodnem smislu in mora biti v nasprotnem položaju.

Reference

1. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.
4. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.
5. Zapata, f. Krožno gibanje. Okreval od: Francesfizike.Blogspot.com.