Domača stran
Fizično
Formule, enačbe in primeri izračuna

Fizično

Formule, enačbe in primeri izračuna

2880
228
Cary Goyette

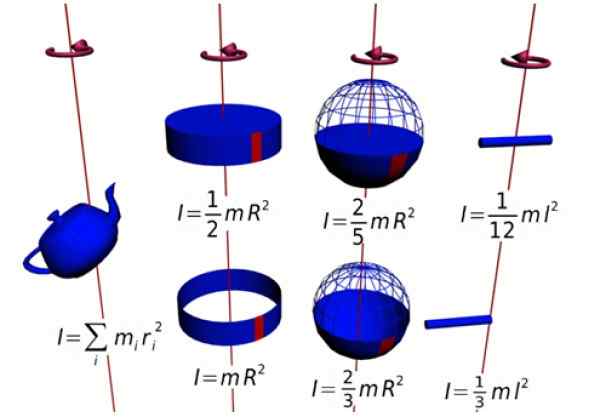
On Inercijski trenutek Od togega telesa glede na določeno osi vrtenja predstavlja njegovo odpornost na spreminjanje njegove kotne hitrosti okoli te osi. Sorazmerna je z maso in tudi z lokacijo rotacijske osi, saj se telo po njegovi geometriji lažje vrti okoli določenih osi kot pri drugih.

Recimo, da je obsežen predmet (sestavljen iz številnih delcev), ki se lahko vrti okoli osi. Recimo, da sila deluje F, tangencialno uporabljen za masni element Δm_Yo, ki ustvari navor ali trenutek, ki ga daje τ_mreža= ∑r_Yo x F_Yo. Vektor r_Yo Je položaj Δm_Yo(Glej sliko 2).

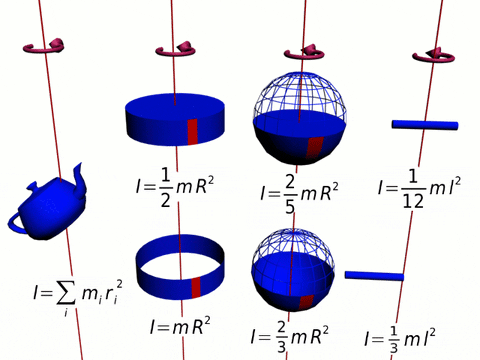Slika 1. Inercije več figur. Vir: Wikimedia Commons.

Ta trenutek je pravokoten na rotacijsko ravnino (naslov +K = zapuščanje papirja). Ker sta trdnost in radialni položaj vedno pravokotna, križni izdelek ostane:

τ_mreža = ∑ f_Yo r_Yo k = ∑ (Δm_Yodo_Yo) r_Yok = ∑ Δm_Yo(do_Yo r_Yo) k

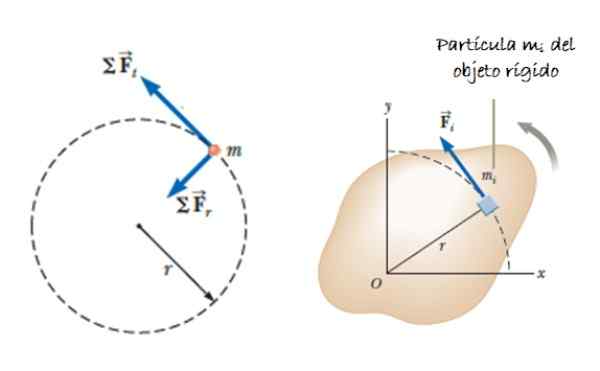Slika 2. Delček, ki pripada togi trdni snovi v rotaciji. Vir: Serway, r. 2018. Fizika za znanost in inženiring. Zvezek 1. Cengage učenje.

Pospešek a_Yo predstavlja tangencialno komponento pospeška, saj radialni pospešek ne prispeva k navoru. Glede na kotni pospešek α lahko navedemo, da:

do_Yo = α r_Yo

Zato je neto navor tak:

τ_mreža = ∑ Δm_Yo(α r_Yo²) K = (∑ r_Yo² Δm_Yo) α k

Kotni pospešek α je enak za celoten objekt, zato nanj ne vpliva podpis "I" in lahko zapusti vsoto, kar je prav trenutek vztrajnosti simboliziranega predmeta s črko I:

I = ∑ r_Yo² Δm_Yo

To je trenutek vztrajnosti diskretne množične porazdelitve. Ko je porazdelitev neprekinjena, se vsota nadomesti z integralom in Δm postane množična diferencial Dm. Integral je narejen nad vsem predmetom:

I = ∫_M(r²) Dm

Enote inercijskega trenutka v mednarodnem sistemu, če so kg x m². Je skalarna in pozitivna količina, saj je produkt testa s kvadratom na daljavo.

[TOC]

Primeri izračuna

Podaljšani predmet, kot so vrstica, disk, sfera ali drugo, čigar gostota ρ Konstantno je in vemo, da je gostota količnik mase - volumna, masna diferencialna Dm Napisano je kot:

ρ = dm/dv → dm = ρDV

Zamenjava v integralu za inercijski trenutek, imamo:

I = ∫r² ρdv = ρ ∫r²DV

To je splošen izraz, veljaven za tridimenzionalni objekt, katerega zvezek V in položaj r So funkcije vesoljskih koordinat x, in in z. Upoštevajte, da je gostota konstantna iz integrala.

Gostota ρ Znana je tudi kot volumetrična gostota, če pa je predmet zelo ravna, kot list ali zelo tanek in ozka kot palica, lahko uporabimo druge oblike gostote, poglejmo:

Vam lahko služi: gibanje za vrtenje zemlje

- Za zelo lep list je gostota, ki jo je treba uporabiti, σ, površinska gostota (masa na enoto površine) in daje je diferencialno območje.

- In če gre za tanko palico, kjer je ustrezna le dolžina, se uporablja linearna gostota mase λ in diferencial dolžine glede na osi, ki se uporablja kot referenca.

V naslednjih primerih se vsi predmeti štejejo za toge (ne -uresničijo) in imajo enakomerno gostoto.

Vztrajnost tanke palice glede na osi, ki poteka skozi njegovo središče

Tu bomo izračunali vztrajnostni moment tanke, toge, homogene palice, dolžine L in mase M, glede na osi, ki poteka skozi sredstva.

V prvi vrsti je treba vzpostaviti koordinatni sistem in zgraditi figuro z ustrezno geometrijo, kot je ta:

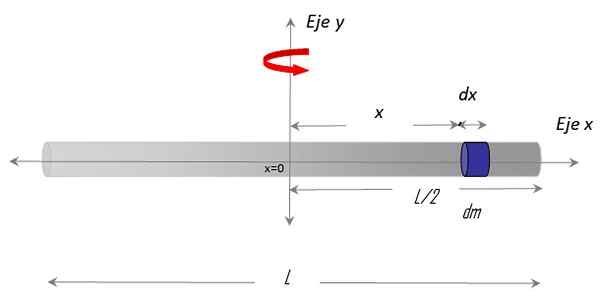Slika 3. Geometrija za izračun vztrajnosti tanke palice glede na navpično osi, ki poteka skozi njegovo središče. Vir: f. Zapata.

Izbran je bil Os x vzdolž lokala in Os y kot rotacijska os. Postopek za vzpostavitev integrala zahteva tudi izbiro množične diferenciala na palici, imenovano Dm, ki ima diferencialno dolžino Dx in se nahaja v položaju x samovoljno glede na center x = 0.

Glede na definicijo linearne gostote mase λ:

λ = m/l

Kadar je gostota enakomerna, kar velja za M in L, je tudi za DM in DX:

λ = dm/dx → dm = λdx.

Po drugi strani je masni element v položaju x, Nato z zamenjavo te geometrije v definiciji imamo določen integral, katerega omejitve so skrajnosti palice v skladu s koordinatnim sistemom:

$I=\int _Mr^2dm =\int_\frac-L2^\fracL2x^2\lambda dx=\lambda \left [\fracx^33 \right ]_\frac-L2^\fracL2=\frac\lambda 3\left [ \fracL^38-\left ( \frac-L^38 \right ) \right ]=\frac\lambda 12L^3$

Zamenjava linearne gostote λ = m/l:

$I=\frac112ML^2$

Če želite najti trenutek inercije palice glede na drugo osi vrtenja, na primer tisto, ki prehaja skozi enega od njegovih koncev Prikazano tukaj, vendar pravilno spreminjanje geometrije.

Momen inercije albuma glede na osi, ki poteka skozi njeno središče

Zelo tanek album, debele debeline, je ravna figura. Če je testo enakomerno razporejeno po celotnem območju A, je masna gostota σ:

σ = M/a

Zelo Dm kot daje ustreza masi in območju diferencialnega obroča, prikazanega na sliki. Domnevali bomo, da se celoten komplet vrti okoli osi in.

Lahko si predstavljate, da je album sestavljen, da veliko radijskih koncentričnih obročev r, vsak s svojim inercijskim trenutkom. Dodajanje prispevkov vseh obročev, dokler ne pridete do radia R, Imeli boste skupno inercijo albuma.

σ = dm/da → dm = σdaje

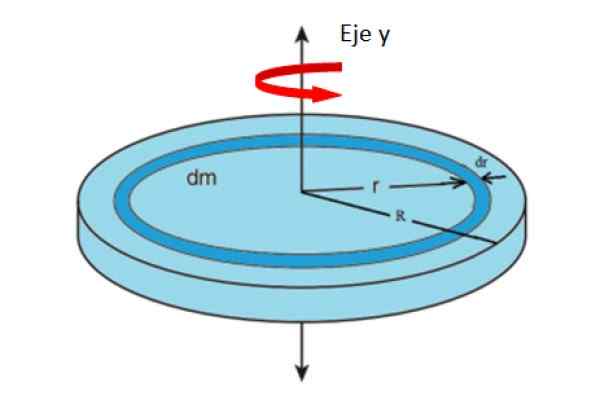Slika 4. Geometrija za izračun inercijskega trenutka albuma glede na osno osi. Vir: f. Zapata.

Kjer m predstavlja celotno testo albuma. Območje albuma je odvisno od njegovega polmera r kot:

Vam lahko služi: hitrost širjenja vala

A = π.r²

Izpeljava o r:

Da /dr = 2 = 2π.R → da = 2π.rdr

Zamenjava zgornjega v definiciji I:

$I=\int _Mr^2dm=\int_0^Rr^2\left (\sigma dA \right )=\sigma \int_0^Rr^2\left (2\pi rdr \right )=2\pi \sigma \int_0^Rr^3dr$ Po oceni integralnih rezultatov:

$I=2\pi \sigma \fracR^44$

Zamenjava σ = m/(π.R²) je ostalo:

$I=2\pi \sigma \fracR^44=2\pi\left (\fracM\pi R^2 \right )\left (\fracR^44 \right )=\frac12MR^2$

Inercijski moment trdne krogle glede na premer

Sferi polmera R lahko štejemo za niz zloženih diskov drug na drugega, kjer vsak neskončni masni album Dm, radio r in debelino Dz, Ima trenutek vztrajnosti, ki ga daje:

dal_disk = (½) r²Dm

Da bi našli to diferencial, je bila formula prejšnjega odseka preprosto vzeta in zamenjana M in R mimo Dm in r, oziroma. Takšen album je mogoče videti v geometriji slike 5.

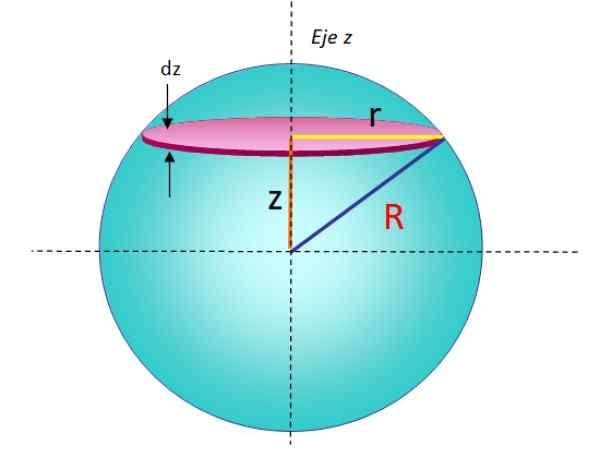Slika 5. Geometrija za izračun vztrajnosti trdnega polmera glede na osi, ki poteka skozi premer. Vir: f. Zapata.

Z dodajanjem vseh trenutkov neskončne inercije zloženih diskov dobimo trenutek popolne vztrajnosti krogle:

Yo_kroglo = ∫di_disk

Ki je enakovredno:

I = ∫_kroglo(½) r²Dm

Če želite rešiti integral, morate izraziti Dm pravilno. Kot vedno je dosežena iz gostote:

ρ = m/v = dm/dv → dm = ρ.DV

Obseg diferencialnega diska je:

DV = osnovno območje x višina

Višina albuma je debelina Dz, Medtem ko je osnovno območje πr², Zato:

DV = πr²Dz

In nadomeščanje v integrirani bi bilo takšno:

I = ∫_kroglo(½) r²Dm = ∫ (½) r²(ρπr²Dz)

Toda pred integracijo se mora. Skozi teorem pitagore:

R² = r² + z² → R² = R² - z²

To nas vodi do:

I = ∫_kroglo(½) ρ r²(πr²dz) = ∫_kroglo(½) ρ π r⁴Dz= ∫_kroglo(½) ρ π (r² - z²)² Dz

Za integracijo celotne sfere opažamo, da se Z razlikuje med -r in R, torej:

$I=\frac12\pi \rho \left [\int_-R^RR^4dz-\int_-R^R2R^2z^2dz+\int_-R^Rz^4dz \right ]$
$I=\frac12\pi \rho \left [R^4z-2R^2\left (\fracz^33 \right )+\fracz^55 \right ]_-R^R=\frac815\pi \rho R^^5$

Vedeti to ρ = m/v = m/[(4/3) πr³] Končno ga dobimo po poenostavitvi:

$I=\frac815\pi \left (\fracM\frac43\pi R^3 \right )R^5=\frac25MR^2$

Inercijski moment trdnega valja glede na osno osi

Za ta objekt se uporablja metoda, podobna tisti, ki se uporablja za kroglo r, debelina Doktor in višina H, Kot da bi bili plasti čebule.

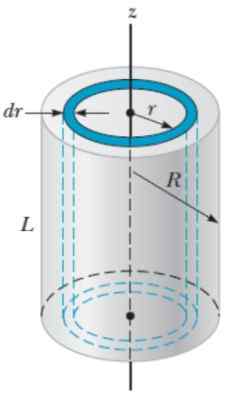Slika 6. Geometrija za izračun vztrajnosti inercije trdnega polmera jeklenke r spoštovanje do osne osi. Vir: Serway, r. 2018. Fizika za znanost in inženiring. Zvezek 1. Cengage.

Glasnost DV cilindrične plasti je:

DV = 2π.Rl.Doktor

Zato je kaskaronska masa:

Vam lahko služi: mikroskopska lestvica: lastnosti, štetje delcev, primeri

Dm = ρ.Dv = ρ. 2π.r.L.Doktor

Ta izraz je nadomeščen v definiciji vztrajnostnega trenutka:

$I=\int _Mr^2dm = \int_0^Rr^22\pi \rho Lrdr=2\pi \rho L\int_0^Rr^3dr=2\pi \rho L\left (\fracR^44 \right )$ Glede na to ρ = m / (π.R²L) je ostalo:

$I=2\pi \left (\fracM\pi R^2L \right ) L\left (\fracR^44 \right )=\frac12MR^2$

Prejšnja enačba kaže, da vztrajnost valja ni odvisen od njegove dolžine, ampak samo od njegove mase in polmera. Ja L spremenjen, bi bil vztrajnost glede na osno osi še naprej enak. Zaradi tega razloga, Yo valja sovpada s tistim iz prej izračunanega tankega albuma.

Inercijski moment pravokotnega lista glede na osi, ki poteka skozi njegovo središče

The Os y Vodoravno kot rotacijska os. Spodnja slika prikazuje potrebno geometrijo za izvajanje integracije:

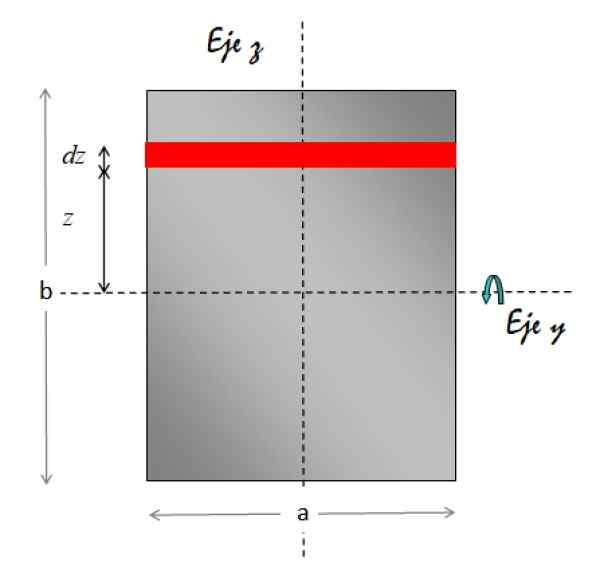Slika 7. Geometrija za izračun inercije inercije pravokotne plošče glede na vzporedno osi do lista in ki poteka skozi njegovo središče. Vir: f. Zapata.

Območni element, prikazan v rdeči barvi, je pravokoten. Njeno območje je torej osnovna višina x, torej:

da = a.Dz

Zato je množična razlika:

Dm = σ.da = σ.(do.Dz)

Kar zadeva razdaljo elementa območja do rotacijske osi, je vedno z. Vse to nadomestimo v integralu inercijskega trenutka:

$I=\int _Mz^2dm=\int_\frac-b2^\fracb2z^2\left (\sigma adz \right )=\sigma a\int_\frac-b2^\fracb2z^2dz=\sigma a\left [ \fracz^33 \right ]_\frac-b2^\fracb2=\frac112\sigma ab^3$

Zdaj gostota površinske mase σ nadomesti::

σ = m/ab

In vsekakor je tako:

$I=\frac112\sigma ab^3=\frac112\left ( \fracMab \right )ab^3=\frac112Mb^2$

Upoštevajte, da je kot tanka palica.

Vztrajnost kvadratnega lista glede na osi, ki poteka skozi njegovo središče

Za kvadrat na strani L, V prejšnjem izrazu, ki velja za pravokotnik, vrednost b po enem L:

$I=\frac112ML^2$

Teoremi inercije

Obstajata dva posebej koristna teorema za poenostavitev izračuna inercijskih trenutkov glede na druge osi, kar bi sicer lahko zapletelo, če bi našli pomanjkanje simetrije. Ti teoremi so:

Steinerjev teorem

Tudi poklican Teorem vzporedne osi, Navede inercijski trenutek glede osi z drugo, ki gre skozi sredino mase predmeta, dokler so osi vzporedne. Če ga želite uporabiti, je treba razdaljo D poznati med dvema osi in seveda maso m predmeta.

Biti Yo_zinercijski trenutek razširjenega predmeta glede na Z, osi_CmInercijski moment glede na osi, ki poteka skozi masni center (cm) omenjenega predmeta, potem je izpolnjeno:

Yo_z = I_Cm + Md²

Ali v zapisu naslednje slike: Yo_z = I_z + Md²

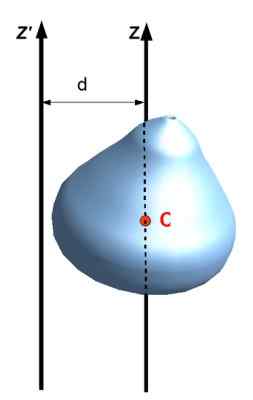Slika 8. Steinerjeva teorem ali vzporedne osi. Vir: Wikimedia Commons. Jack SEE [CC BY-SA (https: // CreativeCommons.Org/licence/by-sa/3.0)]

Teorem pravokotne osi

Ta teorem velja za ravne površine in pravi: Moment inercije ravnega predmeta okoli osi, pravokotne na njej, je vsota vztrajnosti okoli dveh osi, pravokotnih na prvo osi:

Yo_z = I_x + Yo_in

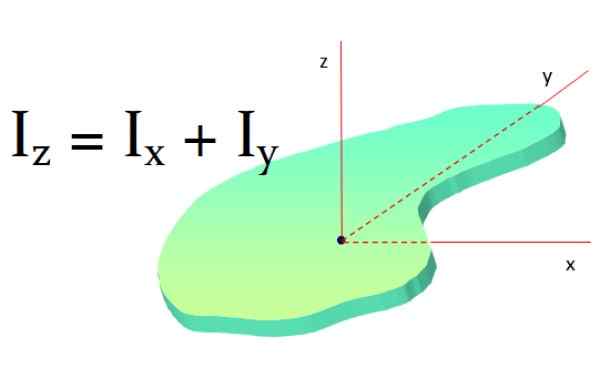Slika 9. Teorem pravokotne osi. Vir: f. Zapata.

Če ima predmet tako simetrijo Yo_x in Yo_in So enaki, potem se izpolni:

Yo_z = 2i_x

Vaja rešena

Poiščite inercijski moment palice glede na osi, ki poteka skozi enega od njegovih koncev, na primer tistega, ki je prikazan na sliki 1 (spodaj in na desni) in slika 10.

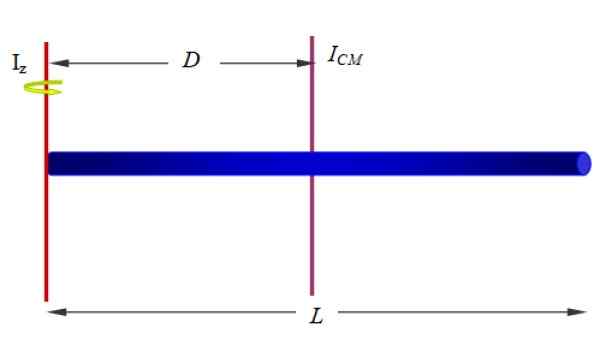Slika 10. Vztrajnost homogene palice okoli osi, ki gre skozi en konec. Vir: f. Zapata.

Rešitev:

Že imamo vztrajnostni trenutek okoli osi, ki poteka skozi njeno geometrijsko središče. Ker je palica homogena, je v tem trenutku njegovo središče mase, tako da bo to naše Yo_Cm Za uporabo Steinerjevega teorema.

Če je dolžina palice L, Os z je na razdalji d = l/2, torej:

Yo_z = I_Cm + Md²= (1/12) ml²+M (l/2)²= (1/3) ml²

Reference

Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill. 313-340
Rex, a. 2011. Osnove fizike. Pearson. 190-200.
Teorem vzporedne osi. Okrevano od: hiperfizika.PHY-ASST.GSU.Edu.
Serway, r. 2018. Fizika za znanost in inženiring. Zvezek 1. Cengage.
Univerza Sevilla. Moment inercije sferičnih trdnih snovi. Okreval od: laplace.nas.je.
Univerza Sevilla. Inercijski trenutek sistema delcev. Okreval od: laplace.nas.je.
Wikipedija. Teorem vzporedne osi. Pridobljeno iz: v.Wikipedija.org