Fermat omeji, kaj je sestavljeno, in rešene vaje

On Fermat meja To je numerična metoda, ki se uporablja za doseganje vrednosti naklona črte, ki je tangentna za določeno funkcijo njegove domene. Uporablja se tudi pri pridobivanju kritičnih točk funkcije. Njegov izraz je opredeljen kot:

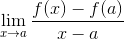
Očitno je, da Fermat ni poznal temeljev izpeljave, vendar so njegove študije spodbujale skupino matematikov, da bi se pozanimale o tangentnih linijah in njihovih aplikacijah v izračunu.

[TOC]

Kaj je Fermatova meja?

Sestavljen je iz pristopa 2 točk, ki v prejšnjih pogojih tvori linijo sekata do funkcije s presečiščem v parih vrednosti.

Ko se približa spremenljivki do vrednosti "A", je par točk dolžan izpolniti. Na ta način postane predhodno suha črta tangentna do točke (a; f (a)).

Vrednost količnika (x - a), ko jo ocenimo v točki "a", vrže nedoločnost omejitev tipa K med ničlo (K/0). Kjer je mogoče te nedoločeve mogoče razbiti z različnimi tehnikami faktorizacije.

Najbolj uporabljene tehnike delovanja so:

-Kvadratna razlika (a² - b² ) = (a + b) (a - b); Obstoj elementa (A-B) v večini primerov pomeni dejavnik, ki poenostavi izraz (x-a) v mejnem razmerju Fermat.

- Kvadratni zaključek (sekira² + bx); Po dokončanju kvadratov dobimo Newton Binomial, kjer je eden od njegovih dveh dejavnikov poenostavljen z izrazom (x - a), ki prekine nedoločnost.

- Konjugat (a + b) / (a ​​+ b); Pomnožite in razdelite izraz s konjugatom nekega faktorja lahko v veliko pomoč pri prekinitvi nedoločenja.

- Skupni dejavnik; V mnogih primerih je rezultat uporabe števca fermata f (x) - f (a), skritih na faktor (x - a), potreben za faktorizacijo. Za to natančno opazimo, kakšni elementi se ponavljajo v vsakem faktorju izraza.

Aplikacija Fermat Limit za največjo in najmanjšo

Tudi kadar Fermatova meja ne razlikuje med največjo in najmanjšo.

Osnovno znanje o grafični teoriji funkcij v teoremu lahko zadostuje za določitev največjih in najmanjših vrednosti med funkcijami. Dejansko je mogoče pregibne točke določiti s teoremom dodatne povprečne vrednosti Fermatovega teorema.

Kubična prispodoba

Najpomembnejši paradoks za fermat je prišel pri preučevanju kubične prispodobe. Ker je bila njegova pozornost usmerjena v tangentne linije funkcije za določeno točko, je naletel na problem definiranja omenjene tangentne črte na obstoječi točki pregiba v funkciji.

Zdelo se je nemogoče določiti tangentno črto do točke. Tako se začne preiskava, ki bi povzročila diferencialni računalnik. Nato opredeljeni s pomembnimi eksponenti matematike.

Maksimus in minimalno

Študija največje in najmanjše funkcije je bila izziv za klasično matematiko, kjer nedvoumna in praktična metoda za njihovo opredelitev.

Fermat je ustvaril metodo, ki temelji na delovanju majhnih diferencialnih vrednosti, ki se po faktorizacijskih procesih odpravijo z največjo potjo in minimalno vrednostjo.

To spremenljivko je treba ovrednotiti v prvotnem izrazu, da se določi koordinata omenjene točke, ki bo skupaj z analitičnimi merili opredeljena z največjim ali najmanjšim izrazom.

Metoda

Fermat v svoji metodi uporablja vieto dobesedno simboliko, ki je bila sestavljena iz izključne uporabe kapitalskih črk: samoglasnikov, za neznanke in soglasnike za znane količine.

V primeru radikalnih vrednosti je Fermat izvedel določen postopek, ki bi ga kasneje uporabili pri faktorizacijah omejitev nedoločenja neskončnost med neskončnostjo.

Ta postopek je sestavljen iz delitve vsakega izraza z uporabljeno diferencialno vrednostjo. V primeru Fermata je uporabila črko E, kjer po delitvi med največjo močjo E postane vrednost, iskana iz kritične točke.

Zgodovina

Fermatova meja je v resnici eden najmanj priznanih prispevkov na dolgem seznamu matematika. Njegove študije so bile iz najpomembnejših številk, da bi v bistvu ustvarili podlage za izračun.

Fermat je bil znan po svojih ekscentričnosti v zvezi s svojimi hipotezami. To je bilo običajno za nekakšen izziv drugim matematikom, ko je že imel rešitev ali demonstracijo.

Imela je veliko različnih sporov in zavezništev z različnimi matematiki, ki so ljubili ali sovražili sodelovati z njim.

Njegov zadnji izrek je bil glavni odgovoren za svojo svetovno slavo, kjer je dejal, da je posploševanje Teorem za pitagore Za katero koli "n" stopnjo je bilo nemogoče. Rekoč, da je to veljavno demonstriral, vendar je umrl, preden je objavil.

Ta demonstracija je morala počakati približno 350 let. Leta 1995 sta matematika Andrew Wiles in Richard Taylor končala tesnobo, ki jo je zapustil Fermat, kar je pokazalo, da je bil prav z veljavno demonstracijo zadnjega izrekanja.

Vaje

Vaja 1

Določite naklon črte tangente na krivuljo f (x) = x² Na točki (4, 16)

Zamenjava v izrazu meje fermata imate:

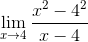
Nato je uporaba kvadratnih minimumov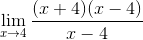

Dejavniki so poenostavljeni (x - 4)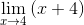

Pri ocenjevanju imate

M = 4 + 4 = 8

Vaja 2

Določite kritično točko izražanja f (x) = x² + 4x z uporabo meje fermata

V tem primeru ni nobene koordinate, zato je vrednost x nadomeščena z generičnim obrazcem x₀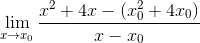

Izvede se strateško združevanje elementov, ki si prizadeva za združevanje vrstnikov X-X₀

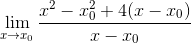
Kvadri so razviti

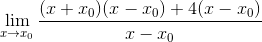
Opazimo skupni faktor X-X_{0 in je izvlečen}

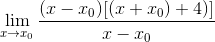
Izraz je že mogoče poenostaviti in nedoločitev je pokvarjena

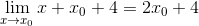
V minimalnih točkah je znano, da je naklon tangentne črte enak nič. Na ta način se lahko ujemamo z ničlo najdeno in razčistimo vrednost x₀    

2 x₀ + 4 = 0

X₀ = -4/2 = -2

Če želite dobiti manjkajočo koordinato, morate oceniti točko v prvotni funkciji

F (-2) = (-2)² + 4 (-2) = 4 - 8 = - 4

Kritična točka je P (-2, -4).

Reference

1. Prava analiza. Zgodovinski pristop Sauhl Stahl, John Wiley & Sons, 5. avgust. 1999.
2. Matematična kariera Pierra avtorja Fermata, 1601-1665: druga izdaja. Michael Sean Mahoney. Princeton University Press, 5. junij. 2018
3. Od Fermata do Minkowskega: Predavanja o teoriji števil in njegovega zgodovinskega razvoja. W. Scharlau, h. Opolka, Springer Science & Business Media, 1985
4. Fermatov zadnji teorem: genetski uvod v teorijo algebrskih številk. Harold m. Edwards. Springer Science & Business Media, 14. januarja. 2000
5. Fermat Days 85: Matematika za optimizacijo. J.-B. Hiriart-Urutie Elsevier, 1. januarja. 1986