Kirchhoff zakon

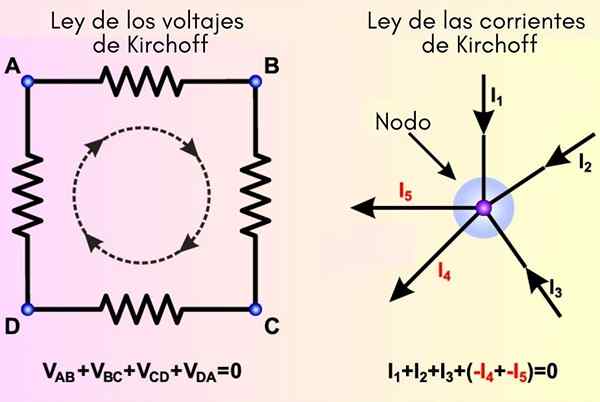
Kirchoffovi zakoni izhajajo iz načel energije in ohranjanja obremenitve. Na levi strani je ustanovljen zakon mrež in na desni tokovi

Kaj so Kirchoffovi zakoni?

The Kirchoff zakon Sestavljajo se iz uporabe načela ohranjanja električnega naboja in načela ohranjanja energije v električnih vezjih, da bi rešili tiste, ki imajo več mrež.

Ta pravila, ker niso zakoni v strogem smislu, so posledica nemškega fizika Gustava Kirchoffa (1824-1887). Njegova uporaba je bistvenega pomena, če zakon OHM ni dovolj za določitev napetosti in tokov v vezju.

Pred izjavo in uporabo Kirchoffovih zakonov se je primerno zapomniti pomena nekaterih pomembnih konceptov na električnih vezjih:

• Vozlišče: Union točka med dvema ali več prevodnimi žicami.
• Podružnica: Elementi vezja, ki sta med dvema zaporednima vozliščema, skozi katere kroži isti tok.
• Mreža: Trajectory ali zaprta zanka, sestavljena iz dveh ali več vej in to se potuje v isto smer, ne da bi šli skozi isto točko.

Kirchoffov prvi zakon

Znan je tudi kot zakon tokov ali vladavine vozlišč in ugotovi, da:

Vsota tokov, ki vstopajo v vozlišče, je enaka vsoti tokov, ki izhajajo iz njega.

Torej je na matematičen način prvi zakon izražen kot:

∑ i = 0

Kjer simbol σ označuje vsoto.

Prejšnja enačba ugotovi, da mora biti celoten tok (obremenitev na enoto časa), ker električni naboj ni ustvarjen ali uničen.

Vam lahko služi: umetni sateliti

Primer

Če želite priročno uporabiti zakon tokov, se v dohodne tokove dodeli znak in nasproten znak za odhodne tokove. Izbira je popolnoma poljubna.

Naslednja slika prikazuje dva toka, ki vstopata v vozlišče, narisana v rdeči: i₁ in jaz₂, in da so pri odhodu prikazani v zeleni: tokovi i₃, Yo₄ in jaz₅.

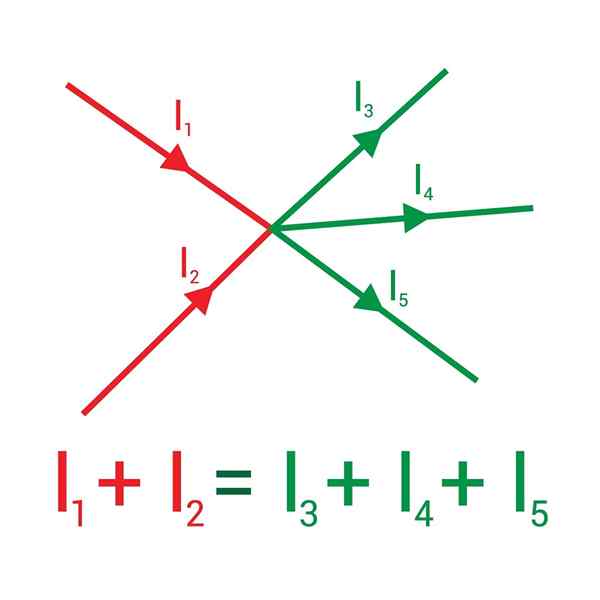Vsota tokov, ki vstopajo v vozlišče, je enaka vsoti tokov, ki izhajajo iz njega

Dodelitev znaka (+) dohodnim tokom in (-) odhodnim, prvo pravilo Kirchoffa ugotovi, da:

Yo₁ + Yo₂ - Yo₃ - Yo₄ - Yo₅= 0 ⇒ I₁ + Yo₂ = I₃ + Yo₄ + Yo₅

Kirchoffov drugi zakon

Druga imena za Kirchoffov drugi zakon so: Zakon o napetosti, Zakon o napetosti tudi Mrežni zakon. Vsekakor to ugotovi, da:

Algebrska vsota napetosti pade vzdolž mrežice, je enaka 0.

To je način za uporabo ohranjanja energije v vezju, saj je napetost v vsakem elementu sprememba energije na enoto obremenitve.

Zato se pri potovanju zaprtega dela (mreže) algebrska vsota napetosti poveča in pade je 0 in ga je mogoče zapisati:

∑ v = 0

Primer

Na naslednji sliki imate mrežo ABCDA, Skozi to je tok v smeri igle ure in pot se lahko začne v kateri koli točki v vezju.

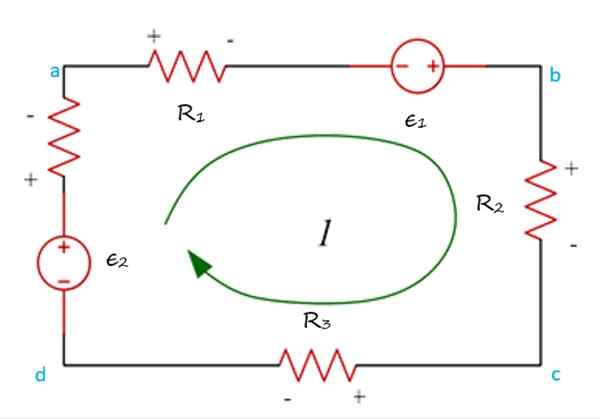Primer mreže, ki je bila gostovana v urniku, kjer se kaže, da povečajo in potencialni padci uporabljajo zakon o napetosti v Kirchoffu. Vir: f. Zapata.

Je tudi potrebno. Običajni je, da se kot pozitivno dodelite napetost, torej ko tok kroži od ( -) do (+). Nato je padec napetosti, ki se pojavi, ko tok preide iz (+) v ( -), negativen.

Vam lahko služi: silicijev oksid (SiO2): struktura, lastnosti, uporabe, pridobivanje

Zagon mrežaste poti v točki "a" je odpor R₁. V njem so obremenitve potencialni padec, ki ga simbolizirajo znaki (+) na levi in ​​( -) nad uporom.

Zato napetost ali napetost v r₁ Ima negativni znak.

Nato dosežete neposredni vir napetosti, imenovan ε₁, katere polarnost je manj (-) Več (+). Tam se električni naboji odpravijo skozi potencialni dvig in ta vir velja za pozitiven.

Po tem postopku za preostali upor in drugi vir se kot rezultat dobi naslednja enačba:

−v₁ + ε₁ - V₂ - V₃ + ε₂ = 0

Kjer v₁, V₂ in v₃ so napetosti v uporu r₁, R₂ in r₃. Te napetosti najdete iz Ohmovega zakona: V = I · R.

Vaja rešena

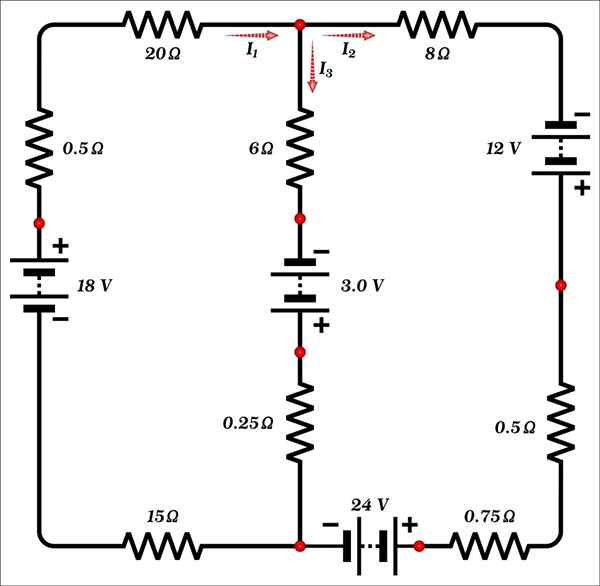
Poiščite vrednost tokov i₁, Yo₂ in jaz₃ prikazano na sliki.

Rešitev

To vezje je sestavljeno le iz dveh mrež in ima 3 neznanke: tokovi in₁, Yo₂ in jaz₃, Torej so potrebne vsaj 3 enačbe za iskanje rešitve.

V vozlišču (točka, označena z rdečo barvo), ki je na vrhu vezja na osrednji veji, opazimo, da tok i₁ je dohodno, medtem ko tokovi I₂ in jaz₃ So odhajajoči.

Zato zakon o Kirchoffovih tokovih vodi v prvo enačbo:

1) i₁ - jaz₂ - jaz₃ = 0

Spodnje vozlišče daje enake informacije, zato je naslednji korak potovati po mrežicah.

Prva mreža

Za vzpostavitev naslednje enačbe se mreža na levi potuje po urniku, začenši z zgornjega levega kot. To je smisel, v katerem krožijo tokovi in ​​tokovi₁ in jaz₃.

Vam lahko služi: optični primerjalnik: Kaj je namenjeno in deli

Upoštevajte to:

• Yo₁ skozi upor 20 Ω, 15 Ω in 0.5 Ω in 18 V baterijo, kjer doživi potencialni dvig.
• S svojim delom₃ Prečka upor osrednje veje 6 Ω in 0.15 Ω in na 3 bateriji.0 V je potencialni dvig.

Prav tako se za določitev napetosti v vsakem uporu uporablja zakon V = i ∙ r, v skladu s tem:

−20 ∙ i₁ - 6 ∙ i₃ + 3.0 - 0.25 ∙ i₃ −15 ∙ i₁ + 18.0 - 0.5 ∙ i₁ = 0

Naročanje pogojev:

(−20 −15 - 0.5) ∙ I₁ - (6 + 0.25) ∙ I₃  = - 3.0 - 18.0

−35.5 ∙ i₁ - 6.25 ∙ i₃ = - 21.0

2) 5 ∙ i₁ + 6.25 ∙ i₃ = 21.0

Druga mreža

Tretja enačba dobimo z ogledom mrežice na desni, začenši v vozlišču vrha vezja. Opazimo, da:

• Yo₂ Pojdite skozi upori 8 Ω, 0.5 Ω in 0.75 Ω, plus 12 V in 24 V baterij. Glede na polarnost baterij je na poti v 12 V porast potenciala in zmanjšanje 24 V.
• Pomembno: Ogled druge mreže (v urniku) nasprotuje i₃, Zato napetosti v uporu 6 Ω in 0.25 Ω so potencialni vzponi in imajo pozitiven znak. Glede na polarnost baterij se v 12 V in pada v 24 V in 3 V.

Z vsem tem dosežete:

−8 ∙ i₂ - 0.5 ∙ i₂ - 0.75 ∙ i₂ + 12.0 - 24.0 + 0.25 ∙ i₃ - 3.0 + 6 ∙ i₃ = 0

3) −25 ∙ i₂ + 6.25 ∙ i₃ = 15.0

Trenutni izračun

Enačbe 1), 2) in 3) tvorijo sistem 3 linearnih enačb s 3 neznanimi, katerih rešitev je:

Yo₁ = 0.381 a; Yo₂ = -0.814 a; Yo₃ = 1.195 a

Negativni znak v trenutnem i₂ pomeni, da teče v nasprotni smeri sheme.