Keplerjevi zakoni Pojasnilo, vaje, eksperimentiranje

The Keplerjevi zakoni O planetarnem gibanju je oblikoval nemški astronom Johannes Kepler (1571-1630). Kepler jih je sklepal na podlagi dela svojega učitelja danskega astronoma Tycho Brahe (1546-1601).

Brahe je podatke skrbno zbral iz planetarnih gibov v več kot 20 letih, s presenetljivo natančnostjo in natančnostjo. Veljavnost vaših podatkov je še danes veljavna.

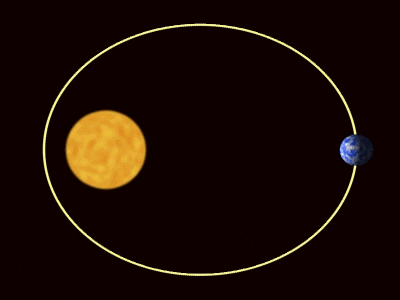Slika 1. Orbite planetov po Keplerjevih zakonih. Vir: Wikimedia Commons. Willow/cc by (https: // creativeCommons.Org/licence/by/3.0

[TOC]

Keplerjevi 3 zakoni

Keplerjevi zakoni določajo:

-Prvi zakon: Vsi planeti opisujejo eliptične orbite s soncem v enem od osvetlitev.

-Drugi zakon ali zakon istega: Črta, usmerjena od sonca do katerega koli planeta (žariščni radio), v enakih časih pomesti enaka območja.

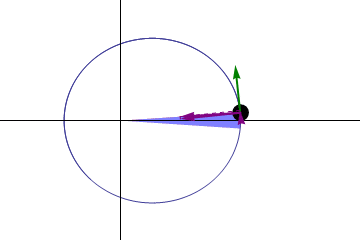Slika 2. Zakon območij. Vir: Wikimedia Commons. Gonfer/CC BY-SA (https: // creativeCommons.Org/licence/by-sa/3.0

-Tretji zakon: Trg časa, ki zavzame katero koli planet orbital okoli sonca, je sorazmeren s kocko njegove povprečne razdalje do sonca.

Biti T Rekel čas, poklican Orbitalno obdobje, in r Povprečna razdalja, potem pa:

T² je sorazmerno z r³

T = k r³

To pomeni, da količnik T²/ r³ Enako je za vse planete, kar omogoča izračun polmera orbitala, če je znano orbitalno obdobje.

Kdaj T Izraženo je v letih in r V astronomskih enotah UA*je konstanta sorazmernosti vredna K = 1:

T²= r³

*Astronomska enota je enaka 150 milijonov kilometrov, kar je povprečna razdalja med Zemljo in soncem. Orbitalno obdobje zemlje je 1 leto.

Univerzalni gravitacijski zakon in Keplerjev tretji zakon

Univerzalni gravitacijski zakon določa, da je velikost gravitacijske sile privlačnosti med dvema masoma M in m oziroma, katerih centri so ločeni na daljavo r, Daje ga:

F = g mm /r²

G je univerzalna gravitacijska konstanta in njegova vrednost je g = 6.674 x 10 ^-enajst N.m²/kg² .

Zdaj so orbite planetov eliptične z zelo majhno ekscentričnostjo.

To pomeni, da se orbita ne premakne veliko stran od kroga, razen v nekaterih primerih, kot je pritlikavi Pluton. Če orbite približamo krožni obliki, je pospešek gibanja planeta:

do_c = v²/r

Glede na F = ma, imajo:

G mm /r² = m.v²/r

Tukaj v To je linearna hitrost planeta okoli sonca, statična in množična predpostavka M, Medtem ko je planet m. Tako:

Vam lahko služi: pomembne številke: pravila, primeri, rešene vaje

To pojasnjuje, da imajo planeti najbolj oddaljeni od sonca nižjo orbitalno hitrost, saj je odvisna od 1/√R.

Ker je razdalja, ki jo potuje planet, približno dolžina oboda: l = 2πr in traja enak čas t, orbitalno obdobje, dobimo:

V = 2πr /t

Izravnava obeh izrazov za V veljaven izraz za T je dosežena², Kvadrat orbitalnega obdobja:

In to je prav tretji zakon Keplerja, saj v tem izrazu oklepaj 4π² /Gm Je torej konstantna T² je sorazmerno z razdaljo r povišana na kocko.

Dokončna enačba za orbitalno obdobje dobimo z ekstrahiranjem kvadratnega korena:

Izračun mase sonca

Koliko je masa sonca? S to enačbo je mogoče ugotoviti. Vemo, da je orbitalno obdobje Zemlje eno leto, polmer orbitala pa 1 UA, kar ustreza 150 milijonov kilometrov, zato imamo vse potrebne podatke.

V naši prejšnji enačbi se razčistimo M, Toda ne preden pretvorite vse vrednosti v mednarodni sistem enot, če:

1 leto = 3.16 x 10⁷ sekunde.

1 ua = 150 milijonov km = 1.5 x10^enajst m.

In z zamenjavo podatkov v enačbi dobimo dokaj uspešno oceno sončnega sonca v 2.0 x 10 ³⁰ kg.

Vaje

Čeprav je imel Kepler v mislih le planete, ko je izhajal iz svojih znanih zakonov, ti veljajo tudi za gibanje satelitov in drugih teles sončnega sistema, kot bomo videli naslednje.

- Vaja 1

Vedeti, da je Jupitrova orbita 5.19 -krat večji kot na Zemlji, poiščite orbitalno obdobje Jupitra.

Rešitev

Po definiciji astronomske enote je Jupiter od sonca 5.19 UA je torej po Keplerjevem tretjem zakonu:

T²= r³= (5.19)³ leta

Zato T = (5.19)^3/2  leta = 11.8 let

- Vaja 2

Halley Comet obišče sonce vsakih 75.3 leta. Najti:

a) Glavno polovico svoje orbite.

b) Ukrep apelija, če perihelij meri 0.568 UA.

Rešitev

Halley Comet obišče sonce vsakih 75.3 leta. Najti:

a) Glavno polovico svoje orbite.

b) Ukrep apelija, če perihelij meri 0.568 UA.

Rešitev

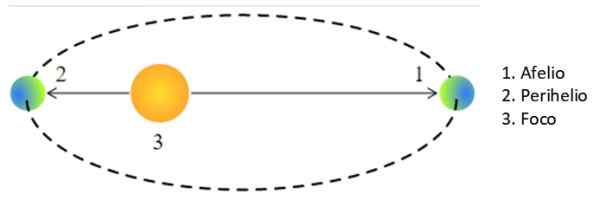
Ko je planet ali katera koli druga zvezda najbližje soncu, se reče, da je v perihelio, In ko je še naprej, v afelion. V posebnem primeru krožne orbite je R v Keplerjevem tretjem zakonu polmer orbite.

Lahko vam služi: Antoine Constants: Formule, enačbe, primeri

Vendar pa je v eliptični orbiti nebesno telo bolj ali manj stran od sonca, saj je polmajor "A" povprečje med aproteso in perihelijem:

Slika 3. Aflio in Perihelio. Vir: Wikimedia Commons. Pearson Scott Foresman / javna domena

Zato nadomestimo r s tretjim zakonom Keplerja, kar ima za posledico Halley v:

T²= a³→ a = (t)²³ → a = (75.3) ²³ Ua = 17.832 UA

Rešitev b

A = ½ (perihelio + apelio)

17.832 = ½ (0.568+ aflio) → aflio = 2 x 17.832 - 0.568 UA = 35.10 UA.

Poskus

Analiza gibanja planetov zahteva tedne, mesece in celo leta skrbnega opazovanja in registracije. Toda v laboratoriju je mogoče izvesti zelo preprost eksperiment, ki dokazuje, da je zakon Keplerja izpolnjen.

Za to je potreben fizični sistem, v katerem je sila, ki ureja gibanje. Tak sistem je sestavljen iz mase, vezane na dolgo vrv, z drugim koncem fiksne niti na podporo.

Testo loči majhen kot njegovega ravnotežnega položaja in je natisnjeno rahlo impulz, tako da izvede ovalno (skoraj eliptično) gibanje na vodoravni ravnini, kot da bi bil planet okoli sonca.

Na krivulji, ki jo opisuje nihalo, lahko dokažemo, da v enakih časih pometa enaka območja, da: da:

-Upoštevamo vektorske radijske sprejemnike, ki segajo od središča privlačnosti (začetna ravnotežna točka) do položaja mase.

-In Barmos med dvema zaporednima trenutkoma enakega trajanja, na dveh različnih območjih gibanja.

Dlje je nihala nit in nižji kot, ki se oddalji od navpične, neto obnovitvena sila bo bolj vodoravna in simulacija spominja na primer gibanja z osrednjo silo v ravnini.

Potem se opisani ovalni približa elipsi, kot je tisto, na katero potujejo planeti.

Materiali

-Neiztežna nit

-1 testo ali kovinska kroglica, pobarvana z belo, ki deluje kot nihalo lečo

-Vladar

-Transporter

-Slikovna kamera z avtomatskim strobom

-Podpira

-Dva vira osvetlitve

-List papirja ali črnega kartona

Lahko vam služi: Teorija velikega krčenja: Zgodovina, načela, podatki za in proti

Postopek

Sklop slike je potreben za fotografiranje več utrinkov nihala, saj sledi njegova usmeritev. Če želite to narediti.

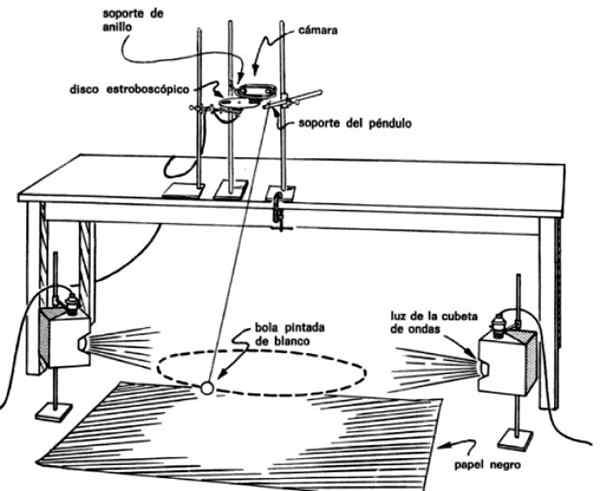Slika 4. Nihalo sklop, da preverite, ali v enakih časih pometa enaka območja. Vir: Vodnik laboratorij PSSC.

Na ta način se slike dobijo v rednih časovnih intervalih nihala, na primer vsakih 0.1 ali vsakega 0.2 sekundi, kar omogoča vedeti, da je potreben čas, ki je bil potreben iz ene točke na drugo.

Prav tako morate priročno osvetliti maso nihala, pri čemer lahko luči postavite na obe strani. Leča mora biti pobarvana bela, da izboljša kontrast na ozadju, ki je sestavljen iz razširjenega črnega papirja na tleh.

Zdaj morate preveriti, ali nihalo v enakih časih pometa enaka območja. Za to je izbran časovni interval in točke, ki jih nihalo zaseda v omenjenem intervalu, so označene na papirju.

Na sliki se črta nariše od središča ovalne do teh točk, zato bomo imeli prvo od območij, ki jih pometa nihalo, ki je približno eliptični sektor, kot je prikazan spodaj:

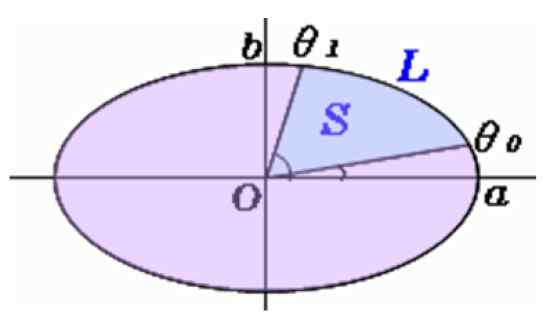Slika 5. Območje eliptičnega sektorja. Vir: f. Zapata.

Izračun območja eliptičnega odseka

Koti se merijo s transporterjem θ_tudi in θ₁, In ta formula se uporablja za iskanje S, območje eliptičnega sektorja:

S = f (θ₁) - f (θ_tudi)

Z F (θ) dobiti od:

Upoštevajte to do in b So polseniji večji in manjši. Bralec bi moral le skrbno meriti polmese in kote, saj obstajajo spletni kalkulatorji za enostavno oceno tega izraza.

Če pa vztrajate, da izračunate ročno, se morate spomniti, da se kot θ meri v stopinjah, vendar ob vstopu podatkov v kalkulator vrednosti morajo biti izražene v radianes.

Nato morate označiti še en par točk, v katere je nihalo vložil v istem časovnem intervalu, in narisati ustrezno območje ter izračunati njegovo vrednost z istim postopkom.

Preverjanje zakona enakih območij

Končno je še vedno preveriti, ali je zakon območij izpolnjen, to je, da se v enakih časih enaka območja pometa.

Ali rezultati nekoliko odstopajo od pričakovanega? Upoštevati morate, da vse ukrepe spremlja njihova eksperimentalna napaka.

Reference

1. Keisan Online Kalkulator. Območje kalkulatorja eliptičnega sektorja. Okreval od: Keisan.Casio.com.
2. OpenTAX. Keplerjev zakon o planetarnem gibanju. Pridobljeno iz: OpenStax.org.
3. PSSC. Laboratorijska fizika. Uredništvo se je vrtelo. Obnovi se od: Knjige.Google.co.
4. Palen, s. 2002. Astronomija. Serija Schaum. McGraw Hill.
5. Pérez r. Preprost sistem z osrednjo silo. Okreval od: Francesfizike.Blogspot.com
6. Stern, d. Trije Keplerjevi zakoni planetalnega gibanja. Okrevano od: phy6.org.