Lenz zakon o formuli, enačbe, aplikacije, primeri

The Lenz zakon Ugotavlja, da je polarnost inducirane elektromotorne sile v zaprtem vezju zaradi variacije pretoka magnetnega polja takšna, da nasprotuje spreminjanju omenjenega toka.

Negativni znak, ki je postavljen na Faradayev zakon, upošteva Lenzov zakon, saj je razlog, zakaj se imenuje zakon Faraday-Lenz in ki je izražen na naslednji način:

Slika 1. Toroidna tuljava lahko sproži tokove pri drugih voznikih. Vir: Pixabay.

[TOC]

Formule in enačbe

ε predstavlja inducirano elektromotorno silo, okrajšano kot Fem, Φ To je pretok magnetnega polja in t Čas je. Enote v mednarodnem sistemu (SI) za Fem So volti (v).

Zaradi svojega dela tok magnetnega polja Φ Opredeljen je z naslednjim skalarnim izdelkom:

Zelo B kot n So vektorske veličine in jih je mogoče označiti s krepko ali s puščico na črki. B Je vektor magnetnega polja in n Je enota vektor (magnitude enaka 1) pravokotni na površino, ki jo prečka B.

V prikazani enačbi B Je konstantna in enota za Φ V SI za pretok magnetnega polja je Weber (W):

1 Weber = 1 Tesla. meter²

Drug način izražanja Φ To je dobimo z uporabo definicije skalarnega izdelka:

Φ = b.Do.cos θ

V tej enačbi, B To je velikost magnetnega polja (brez krepke ali puščice, da ločimo vektor od njegove razsežnosti), a je območje površine, ki jo prečka polje in θ je kot med vektorji B in n.

Tok magnetnega polja se lahko sčasoma spreminja na različne načine, da ustvari Fem induciran v zanki - zaprtega vezja - območja do. Na primer:

-Izdelava magnetnega polja sčasoma: B = B (T), Držite območje in stalen kot, nato pa:

-Območje spaze se lahko razlikuje, tako da ostale velikosti pustijo konstantne:

 -Kot med B In površino je spremenjena z vrtenjem ločitve, na ta način dobimo sinusoidni generator:

Še bolje, če se namesto ene zanke uporablja Nougas, v tem primeru Fem Pomnožite n krat:

 Seveda se lahko pretok magnetnega polja spreminja s katero koli kombinacijo teh oblik, čeprav bi bilo nekoliko bolj zapleteno opisati.

Prijave

Takojšnja uporaba Lenzovega zakona je določiti pomen Fem ali inducirani tok, ne da bi bilo treba izvesti kakršen koli izračun. Upoštevajte naslednje: na sredini magnetnega polja imate zanko, na primer tisto, ki proizvaja magnet.

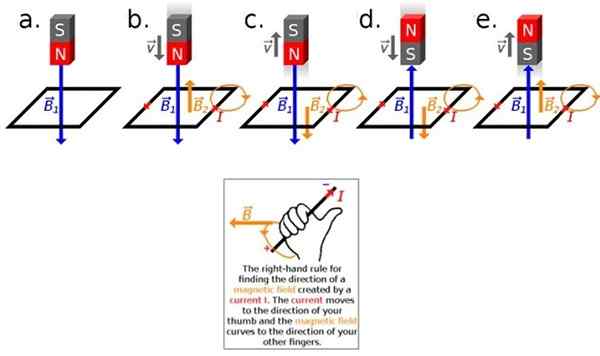Slika 2. Uporaba Lenzovega zakona. Vir: Wikimedia Commons.

Če sta magnet in zanka v mirovanju glede na drugo, se nič ne zgodi, torej ne bo induciranega toka, ker v tem primeru ostane pretok magnetnega polja (glej sliko 2A). Da bi sprožili tok, je potrebno, da se pretok razlikuje.

Če obstaja relativno gibanje med magnetom in spazom, bodisi premika magnet proti ločitvi ali je proti magnetu, bo induciran tok za merjenje (slika 2B naprej).

Ta inducirani tok posledično ustvari magnetno polje, zato bomo imeli dve polji: magnet B₁ v modrem in tistem, povezanem s tokom, ustvarjenim z indukcijo B₂, v oranžni.

Desni vladar palca vam omogoča, da poznate smer B₂, Če želite to narediti, je palec desne roke nameščen v smer in smer, ki jo ima tok. Ostali štirje prsti označujejo smer, v kateri je magnetno polje ukrivljeno, glede na sliko 2 (spodaj).

Vam lahko služi: konveksno ogledalo

Gibanje magneta skozi spase

Recimo, da se magnet spusti proti zanki z njen severnim polom, usmerjenim proti njej (slika 3). Magnetne poljske črte zapustijo severni pol N in vstopijo na južni pol. Torej se bodo spremenile φ, tok, ki ga je ustvaril B₁ ki prečka zanko:Φ poveča!  Zato je v zanki ustvarjeno magnetno polje B₂ Z nasprotnim namenom.

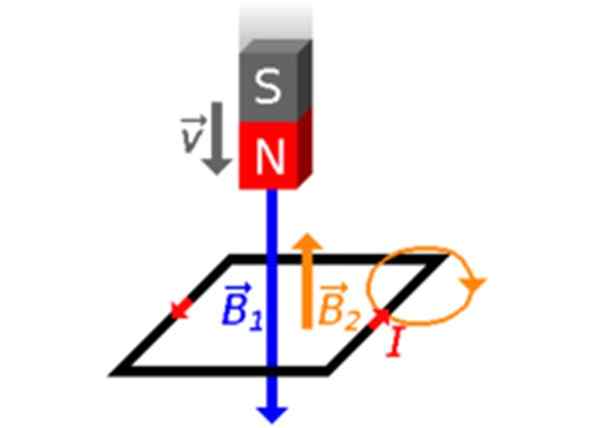Slika 3. Magnet se s svojim severnim polom premakne proti zanki. Vir: Wikimedia Commons.

Inducirani tok je smiselno v nasprotju z iglami uro, -flehas rdeče na slikah 2 in 3-, v skladu z desnim pravilom palca.

Odmaknimo se spiralni magnet in nato njegov Φ zmanjšuje (sliki 2C in 4), zato je zanka v notranjosti hitro ustvariti magnetno polje B₂ Na enak način nadomestil. Zato je inducirani tok čas, kot je razvidno iz slike 4.

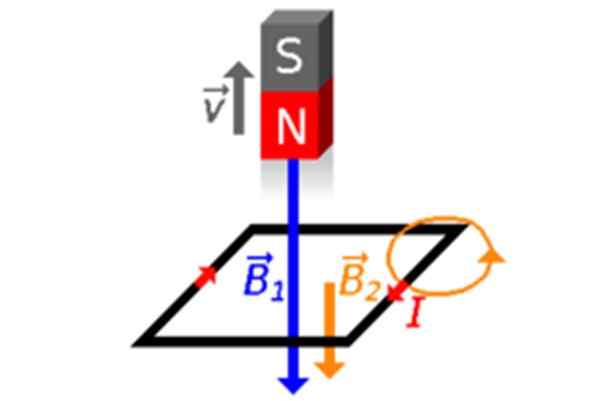Slika 4. Magnet se oddalji od zanke, vedno s svojim severnim polom, ki kaže nanjo. Vir: Wikimedia Commons.

Vlaganje položaja magneta

Kaj se zgodi, če je vložen položaj magneta? Če južni pol pokaže na zanko, polje kaže, saj črte B V magnetu zapustijo Severni pol in vstopijo na Južni pol (glej sliko 2D).

Takoj Lenzov zakon sporoča, da bo to navpično polje, ki se bori proti zanki, pri tem sprožilo nasprotno polje, B₂ navzdol in inducirani tok bo tudi čas.

Končno se odmakne magnet La Espira, vedno s svojim južnim polom, ki kaže na notranjost tega. Potem je znotraj zanke polje B₂ Prispevati k odstranitvi magneta, ki ne spreminja polja v njem. Zelo B₁ kot B₂ Imeli bodo enak pomen (glej sliko 2D).

Bralec se bo zavedal, da, kot smo obljubili.

Poskusi

Heinrich Lenz (1804-1865) je v svoji znanstveni karieri opravljal številna eksperimentalna dela. Najbolj znani so tisto, kar smo pravkar opisali, in se posvetili merjenju sil in magnetnih učinkov, ki jih ustvari magnet sredi zanke. S svojimi rezultati je izpopolnil delo, ki ga je opravil Michael Faraday.

Ta negativni znak v Faradayevem zakonu se izkaže za eksperiment, za katerega je danes najbolj priznan. Vendar je Lenz v mladosti opravljal veliko delov v geofiziki, medtem pa je bil namenjen spuščanju magnetov znotraj zavojev in cevi. Preučeval je tudi električno odpornost in kovinsko prevodnost.

Zlasti na učinke povečanja temperature vrednosti upora. Nenehno je opazil, da se pri segrevanju žice upor zmanjšuje in razprši toploto, kar je tudi James Joule samostojno opazoval tudi James Joule.

Za vedno se spomnite njihovih prispevkov k elektromagnetizmu, poleg zakona, ki nosi njegovo ime, so induktivnosti (tuljave) označene s črko L.

Vam lahko služi: Thévenin teorem: kaj je sestavljeno, aplikacije in primeri

Lenzova cev

To je poskus, v katerem je prikazan kot magnet, ko se sprosti v bakreni cevi. Magnet pri padcu ustvarja razlike v pretoku magnetnega polja znotraj cevi, kot je to primer s spiralo moči.

Nato se ustvari inducirani tok, ki nasprotuje spremembi toka. Cev za to ustvarja svoje magnetno polje, ki je, kot že vemo, povezana z induciranim tokom. Recimo, da se magnet sprosti z južnim polom navzdol (2d in 5).

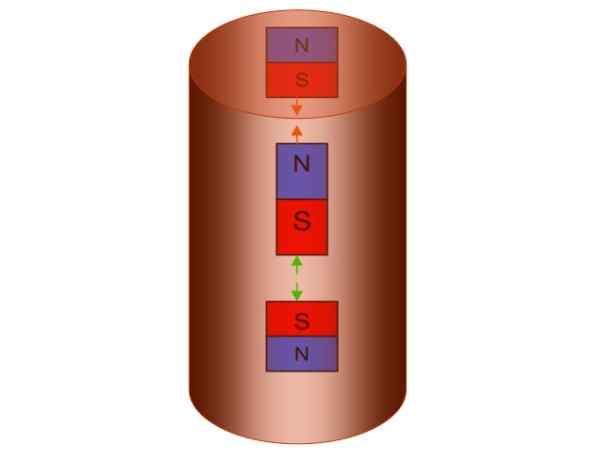Slika 5. Lenzova cev. Vir: f. Zapata.

Kot rezultat, cev ustvari svoje magnetno polje s severnim polom dol In južni pol navzgor, kar je enakovredno ustvarjanju nekaj fiktivnih magnetov, enega zgoraj in drugega pod tistim, ki pada.

Koncept je utelešen na naslednji sliki, vendar je treba zapomniti, da so magnetni drogovi nerazdružljivi. Če ima spodnji fiktivni magnet severni drog navzdol, bo nujno spremljal jug navzgor.

Ko privlačijo nasprotni drogovi in ​​nasprotniki odbijajo, bo magnet, ki pade.

Neto učinek bo vedno zaviral, tudi če se magnet sprosti s severnim polom navzdol.

Joule-Lenz zakon

Zakon Joule-Lenz opisuje kot del energije, povezane z električnim tokom, ki kroži po vozniku, se izgubi v obliki toplote, ki se uporablja v električnih grelnikih, ploščah, sušilnikih za lase in električni peči, med drugimi napravami.

Vsi imajo upor, nitko ali ogrevalni element, ki se segreje do prehoda toka.

V matematični obliki, naj bo to R Odpornost grelnega elementa, Yo trenutna intenzivnost, ki kroži skozi njega in t Čas, količina toplote, ki jo proizvaja Joule Effect, je:

Q = i². R. t

Kje Q Meri se v Joulesu (enote SI). James Joule in Heinrich Lenz sta ta učinek odkrila hkrati okoli leta 1842.

Primeri

Spodaj prikazujemo tri pomembne primere, v katerih se uporablja zakon Faraday-Lenza:

Izmenični tok generator

Generator izmeničnega toka pretvori mehansko energijo v električno energijo. Temelj je bil opisan na začetku: zanko se zasuka na sredini enotnega magnetnega polja, kot je tisto, ki je ustvarjena med obema poljama velikega elektromagneta. Ko se uporablja N spirale, the Fem sorazmerno povečuje N.

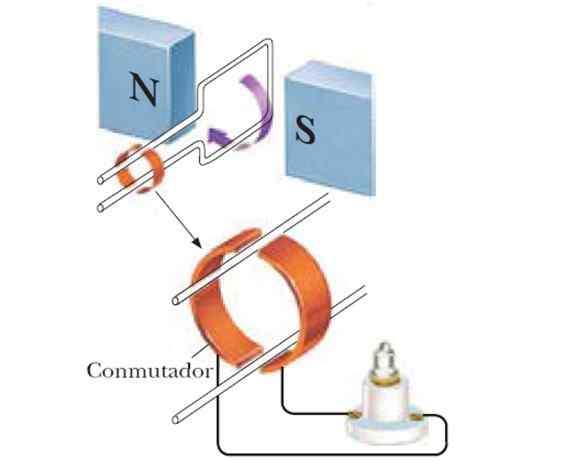Slika 6. Generator izmeničnega toka.

Ko je zanka obrnjena, običajni vektor na svojo površino spremeni svojo orientacijo glede na polje in ustvari a Fem ki se sčasoma razlikuje na sinusoidni način. Predpostavimo, da je kotna frekvenca vrtenja Ω, Potem pa bo pri zamenjavi enačbe, ki se je zgodila na začetku,:

Transformator

To je naprava, ki omogoča pridobivanje neposredne napetosti iz nadomestne napetosti. Transformator je del neštetih naprav, na primer polnilnik mobilnega telefona.Deluje na naslednji način:

Okrog železnega jedra sta valjani dve tuljavi, ena se imenuje primarno in drugo sekundarna.  Ustrezno število krogov je n₁ in n₂.

Primarna tuljava ali navijanje je povezana z nadomestno napetostjo (na primer domača elektrika) V_Str = V₁.cos ωt, povzroči kroženje izmeničnega frekvenčnega toka Ω.

Ta tok izvira iz magnetnega polja, ki posledično povzroči nihajoči magnetni tok v drugi tuljavi ali naviji, s sekundarno napetostjo oblike V_S = V₂.cos ωt.

Vendar se izkaže, da je magnetno polje znotraj železnega jedra sorazmerno z obratnim številom krogov primarnega navijanja:

Lahko vam služi: 13 primerov Newtonovega drugega zakona v vsakdanjem življenju

B ∝ 1 /n₁

In tako bo V_Str, napetost v primarni navijanju, medtem ko Fem inducirano V_S V drugem vijuganju je sorazmerno, kot vemo, s številom zavojev n₂ in tudi do V_Str.

Torej kombiniranje teh sorazmernosti obstaja povezava med V_S in V_Str ki je odvisno od količnika med številom zavojev vsakega, kot sledi:

V_S = (N₂ /N₁) V_Str

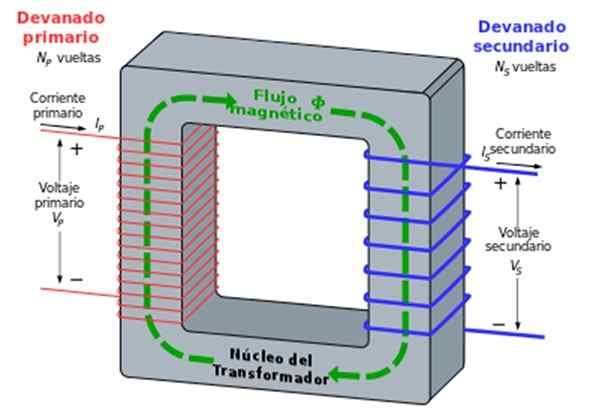Slika 7. Transformator. Vir: Wikimedia Commons. Kundalinizero [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Kovinski detektor

So naprave, ki se uporabljajo v bankah in varnostnih letališčih. Zaznajo prisotnost katere koli kovine, ne samo železa ali niklja. Delujejo po zaslugi induciranih tokov z uporabo dveh tuljav: enega oddajnika in drugega sprejemnika.

V oddajni tuljavi se prenaša izmenični visokofrekvenčni tok, tako da ustvari nadomestno magnetno polje vzdolž osi (glej sliko), ki v sprejemni tuljavi povzroči tok, nekaj bolj ali manj podobno tistemu, kar se zgodi s transformatorjem.

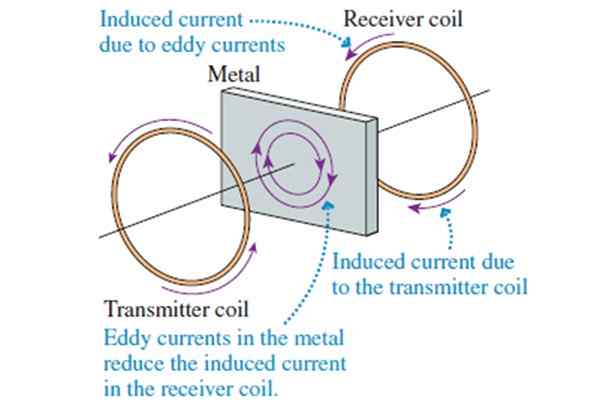Slika 8. Načelo delovanja detektorja kovin.

Če je kos kovine nameščen med obema tuljavama, se v njem pojavijo majhni inducirani tokovi, imenovani Foucault tokovi (ki ne morejo teči v izolatorju). Sprejemna tuljava se odziva na magnetna polja oddajne tuljave in tiste, ki jih ustvarijo Foucaultovi tokovi.

Foucault tokovi poskušajo zmanjšati tok magnetnega polja v kovinskem kosu. Zato se polje, ki zaznava sprejemno tuljavo, zmanjšuje pri prepletu kovinskega kosa med obema tuljavama. Ko se to zgodi alarm, ki opozarja na prisotnost kovine.

Vaje

Vaja 1

Obstaja krožna tuljava s 250 podjetji polmera 5 cm, ki se nahaja pravokotno na magnetno polje 0.2 t. Določiti Fem inducirano, če v časovnem intervalu 0.1 s, magnetno magnetno polje podvoji in kaže na pomen toka, v skladu z naslednjo sliko:

Slika 9. Krožna spira na sredini enakomernega magnetnega polja, pravokotno na ravnino lopatice. Vir: f. Zapata.

Rešitev

Najprej bomo izračunali velikost inducirane FEM, potem bo pomen povezanega toka označen glede na risbo.

N = 250 zavojev

A = π. R² = p . (5 x 10^-2 m)² = 0.0079 m².

cos θ = cos 0 = 1 (Vektor n Potrebno je vzporedno B)

Ko magnetno polje podvoji njegovo velikost, imate:

Zamenjava teh vrednosti v enačbi za velikost Fem Inducirano:

ε = 250. 0.0079 m² . 2 T/S = 3.95 V

Ker se je polje podvojilo, je tudi to pretok magnetnega polja, zato je v zanki ustvarjen inducirani tok, ki nasprotuje omenjenemu povečanju.

Polje na sliki kaže na zaslon. Polje, ki ga ustvari inducirani tok, mora zapustiti zaslon, pri čemer uporabi pravi pravilo palca, iz tega sledi, da je inducirani tok protinosnovni.

Vaja 2

Kvadratno navijanje je sestavljeno iz 40 zavojev 5 cm strani, ki pogosto zavije 50 Hz na sredini enotnega polja z magnitudo 0.1 t. Sprva je tuljava pravokotna na polje. Kakšen bo izraz za Fem inducirano?

Rešitev

Iz prejšnjih razdelkov je bil ta izraz sklenjen:

ε = n.B.Do. Ω. greh ωt

A = (5 x 10^-2 m)² = 0.0025 m²

N = 40 spiralov

Ω = 2π.F = 2π.50 Hz = 100str s^-1

B = 0.1 t

ε = 40 x 0.1 x 0.0025 x 100π  X Sen 50.t =str . Sen 100π.T V

Reference

1. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 6. Elektromagnetizem. Uredil Douglas Figueroa (USB).
2. Hewitt, Paul. 2012. Konceptualna fizikalna znanost. 5. Ed. Pearson.
3. Vitez, r.  2017. Fizika za znanstvenike in inženiring: strateški pristop. Pearson.
4. OpenX College. Faradayev zakon o indukciji: Lenzov zakon. Pridobljeno iz: OpenTextbc.AC.
5. Fizika librettexts. Lenzov zakon. Okrevano od: Phys.Librettexts.org.
6. Sears, f. (2009). University Physics Vol. 2.