Formule zakona o Hooke, primeri, aplikacije, vaje

The Hookejev zakon poudarja, da je deformacija, ki jo doživlja elastični objekt, neposredno sorazmerna z uporabljeno silo na njem. Konstanta sorazmernosti je odvisna od narave predmeta, njegove geometrije in materiala, s katerim je izdelan.

Vsi materiali imajo elastične lastnosti v večji ali manjši meri, zato ustrezajo Hookejevemu zakonu, kadar se vrnejo v prvotne dimenzije, ko sila preneha. Elastični izviri in dlesni so dobri primeri predmetov, ki ustrezajo Hookejevemu zakonu, vendar so tudi jeklene kabile, ki so del mostu.

Slika 1. Hookejev zakon spomladi

Kot primer, da je vzmet ali pristanišče, da ga ohranite raztegnjene ali stisnjene, je treba uporabiti silo, katere velikost je F. Po Hookeovem zakonu bo pomlad doživela deformacijo X:

F ∝ x

Konstanta sorazmernosti, ki se imenuje pomlad pomladna togost, Zato je označen kot k:

F = k⋅x

V enotah mednarodnega sistema je sila v Newtonu (N) in deformaciji v metrih (m). Zato ima vzmetna konstanta n/m enote. Vzmetna konstanta predstavlja silo, ki jo je treba uporabiti za deformiranje v dolžini 1 m.

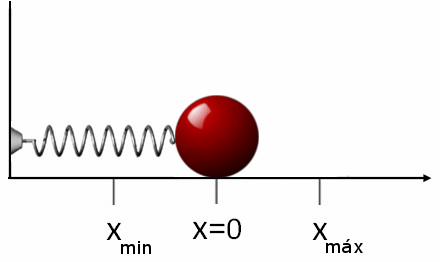Slika 2. Ko se vzmet raztegne, je sila, ki se izvaja na predmetu. Enako se zgodi, če se vzmet skrči, v tem primeru poganja predmet v nasprotnem smislu. Vir: Wikimedia Commons.

Če se po raztezanju ali stiskanju vzmeti sprosti, se bo premaknil v nasprotni smeri do uporabljene sile. To pomeni, da če ga raztegnemo, je stisnjen in obratno. Zato sile F_R to Spomladanske vaje je:

F_R = -k⋅x

Negativni znak kaže na to, kar je rečeno: da sila nasprotuje premiku, zato je ta sila znana kot Obnovitvena sila.

[TOC]

Formula in enačbe

Razmerje med silo in premikom spomladi je odkril Robert Hooke (1635-1703), opazen angleški fizik in znan po svojem rivalstvu z Isaakom Newtonom. Hooke je bil vsestranski znanstvenik, ki se je uspešno spopadel na različnih področjih znanosti: mehanika, biologija, astronomija in arhitektura.

Slika 3. Angleški fizik Robert Hooke, ki ne pozna takratnih portretov. To je rekonstrukcija, ki jo je umetnica Rita Gerer izdelala leta 2004 z opisi, ki so jo pustili tisti, ki so se srečali z znanstvenikom. Vir: Wikimedia Commons. Rita Greer / fal.

Hooke je spoznal, da če sila, ki se nanaša na pomol, ni zelo velika, je dok sorazmerno deformira.

Vam lahko služi: Zemljina magnetosfera: značilnosti, struktura, plini

Na ta način ima Hookejev zakon grafično obliko ravne črte, katere pobočje je vzmetna konstanta. Naslednja slika prikazuje silo, ki je na vzmet, da jo raztegne - ali stisne - odvisno od položaja x. Upoštevajte, da sila ni odvisna od naravne dolžine vzmeti, ampak od njegovega premika.

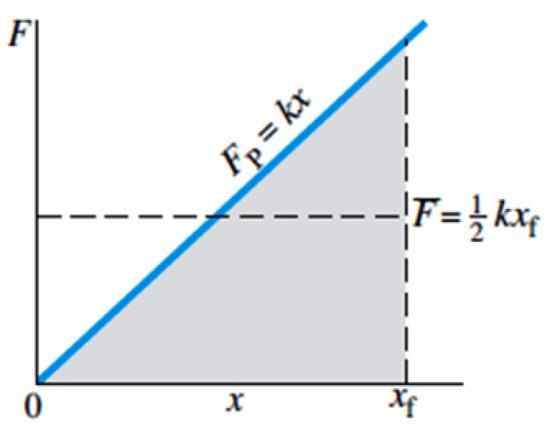Slika 4. Velikost f potrebne sile za raztezanje ali stiskanje vzmeti, odvisno od deformacije X. Vir: Giancoli, D. Fizika z aplikacijami.

Povprečna sila je v grafu označena s f s palico in je enakovredna ½ kx_F, kjer x_F je končni položaj pomladi.

Obe sili, ki se izvajata na pomladi, in sila, ki jo izvaja na predmetu, vezani nanj, sta spremenljivi sili. Bolj ko se želite raztegniti ali stisniti do pomladi, več moči morate uporabiti, da jo lahko dosežete.

Delo, opravljeno za raztezanje ali stiskanje vzmeti

Ko se uporabi sila, ki pomlad deformira, je delo, ki je shranjeno spomladi.

Mehansko delo je opredeljeno kot območje pod grafom sile F, odvisno od položaja x. Za izračun dela s spremenljivo silo f (x) pri premikanju predmeta iz položaja x₁ za pozicioniranje x₂ Določeni integral je treba izračunati:

V primeru dela, ki je potrebno, da se vzmet iz njenega ravnotežnega položaja pripelje do položaja x_F Zelo preprosto je, saj je območje, ki ga je treba izračunati, območje sivega zasenčenega trikotnika slike 4, katerega formula je znana:

Območje trikotnika = ½ osnove. višina

Zato je potrebno delo:

W = ½ x_F . (KX_F) = ½ K (x_F)²

In če želite izračunati potrebno delo, da se do pomladi pripeljete od položaja x do položaja x_F, Na sliki 5 bi bilo enakovredno izračunu območja opraskanega trapeza:

W = ½ k (x_F)² - ½ K x²

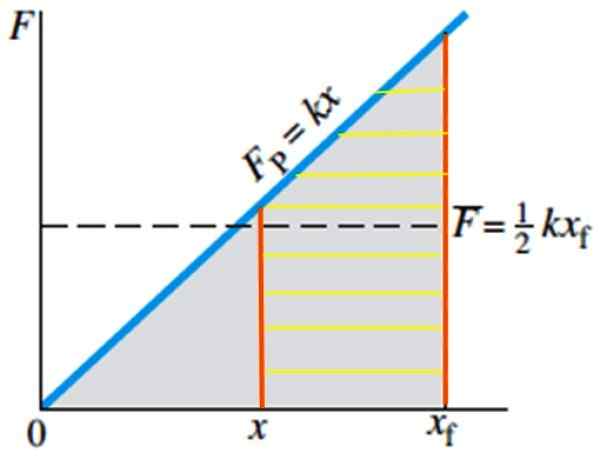Slika 5. Delo, opravljeno za raztezanje pomladi od položaja X do položaja XF, enakovredno območju Rayada. Vir: Giancoli, D. Fizika z aplikacijami.

Primeri izvirov

Glede na aplikacijo, ki ji je namenjena, so lahko vzmeti valjaste, stožčaste, spiralne, s krožnim prerezom (najpogostejšim), kvadratnega ali pravokotnega odseka.

Vam lahko služi: električni vodniki

Široko uporabljena klasifikacija je glede na vrsto truda, za katero bodo podvrženi: tam so torziji, fleksion, stiskanje in razširitve. Slednje se uporabljajo veliko, poleg tega pa delujejo tudi za napetost in stiskanje.

Kompresijska vzmet

Primer kompresijske vzmeti je tisto, kar se uporablja v igrači, imenovani Pogo tudi Saltoín palo. Te vzmeti hranijo precej potencialno energijo, ko se stisnjujejo in se postopoma sproščajo, medtem ko se vračajo v ravnotežni položaj. Na ta način skoki niso preveč nenadni.

Slika 6. Pogo ali saltoín palica temelji na kompresijski vzmet. Vir: Wikimedia Commons.

Podaljšek in torzijske vzmeti

Vzmet za vzmetenje je vrsta podaljškov in so izdelani z dobro zbranimi zavoji, z dvema kljukoma na koncih. Lahko ohranijo dovolj potencialne energije, ki jo pozneje sprostijo, ko se nekdo dvigne in začne skakati po platnu, kar ima tudi svoj elastični odziv, kot vsi materiali.

Torzijske vzmeti so zelo pogoste, saj strežejo za izdelavo oblačil. Namesto kavljev na koncih se upognejo pod kotom, da se upirajo silam, ki ponavadi izvajajo torzijo.

Slika 7. Vzmeti so del neštetih mehanizmov, kot so ta pinceta za oblačila. Vir: Pxfuel.

Materiali za proizvodne vzmeti

Najprimernejši materiali za izvire so tisti z a Končna odpornost (končni odpor), torej podpirajo velik napor, preden se zlomijo. Prav tako je priročno, da ima material visoko točko plazenja, tako da z majhnimi napori ne izgubi svojih elastičnih lastnosti.

Vzmeti industrijske uporabe so izdelani z zlitinami, ki vključujejo jeklo z visoko vsebnostjo ogljika, bakra, niklja in brona.

Prijave Hooke's Law

Ker imajo izviri shranjevanje potencialne energije, ko se raztezajo ali stisnejo, lahko delujejo s premikanjem stvari, kot so mehanizmi.

Na ta način imajo izviri veliko aplikacij, od majhnih in dnevnih predmetov, do avtomobilov, do strojev vseh vrst. Vzmeti služijo:

-Šok vibracije.

-Izdelava izvlečnih mehanizmov: pisalo, viseče pincete, kljuke za lase.

-Naredite pomlad ali dinamometri

In so tudi del mehanizma:

Vam lahko služi: zaprto električno vezje

-Ure.

-Trampolini.

-Ključavnice.

-Igrače.

-Orožje.

-Številke igle, na primer galvanometer, ki se uporablja za merjenje tokov, napetosti in uporov.

Rešene vaje

- Vaja 1

Uporablja se sila magnitude 5.0 N na vzmet, s čimer je dolžina 3 raztezanja.5 cm od naravne dolžine.

a) Koliko se raztegne, ko je uporabljena sila 7 n?

b) Poiščite delo, ki ga opravi uporabljena sila, da se raztegne do pomladi 3.5 cm od naravne dolžine.

Rešitev

Vedeti, da je vzmet raztegnjena 3.5 cm z uporabo 5.0 N Lahko izračunamo vašo konstanto:

k = f / x = 5.0 N / 3.5 cm = 1.43 N / cm.

Ko se uporabi 7 N sila, dobimo naslednji raztežaj:

x = f / k = 7.0 N / 1.43 n/m = 4.9 cm

Rešitev b

Potrebno delo za deformiranje pomladi je podano z:

W = ½ kx² = 0.5 x 1.43 n / cm x (3.5 cm)² = 8.76 n . cm = 8.76 n . 1 x10 ^-2 M = 0.0876 J.

- Vaja 2

Iz podpore visi vzmet zaničevalnega testa in 10 cm dolga. Če je masa 2 kg obešena, se vzmet raztegne, dokler ne doseže 15 cm. Izračunati:

a) vzmetna konstanta

b) Vzmetno velikost, ko je masa 3 kg suspendirana.

Rešitev

Vzmetni raztežaj je x = 15 - 10 cm = 5 cm

Ker je sistem v statičnem ravnovesju, silo, ki jo izvaja vzmet, ko je raztezanje usmerjeno navpično navzgor, kompenzira težo, ki je usmerjena navzdol, nato:

F_R = W → kx = mg

K = 2 x 9.8 N / 5 x10 ^-2 M = 392 n/m

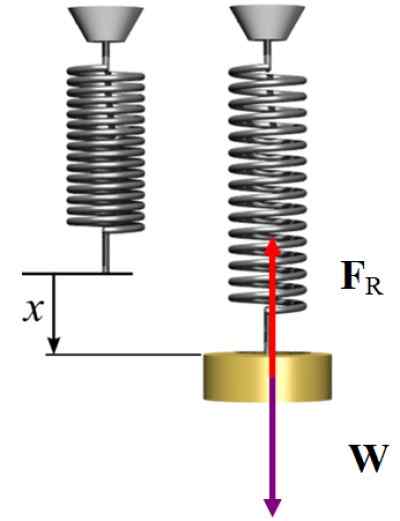Brezplačen karoserijski diagram za vajo razrešen 2. Vir: Wikimedia Commons/F. Zapata.

Rešitev b

Ko je 3 kg teža suspendirana, je nova sila w = 3 x 9.8 n = 29.4 n

V tem primeru je raztežaj:

x = mg /k = 29. 4 n / 392 n / m = 0.075 M = 7.5 cm

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Blog ustvarjalnih mehanizmov. Štiri različne vrste vzmeti. Okrevano od: kreativemehanizmi.com.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 2. Dinamično. Uredil Douglas Figueroa (USB).
4. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed. Dvorana Prentice.
5. Vitez, r.  2017. Fizika za znanstvenike in inženiring: strateški pristop.  Pearson.