Hess Pojasnilo zakon, aplikacije, primeri

The Hess zakon To je še ena manifestacija zakona o ohranjanju energije, ki omogoča določitev s preprostimi algebrskimi vsotami entalpijo kemijske reakcije. Entalpija, ki se razume kot toplota, ki se sprošča ali absorbira, pri konstantnem tlaku, kar je povezano s kakršno koli kemijsko reakcijo ali kemičnim pojavom.

Entalpije, ΔH, se eksperimentalno določijo z uporabo kalorimetrije. Vendar obstajajo reakcije, ki jih je težko preučiti s to tehniko. Ko se to zgodi, se uporabljajo tudi druge reakcije, ki jih imajo njihove posebne entalpije in imajo interese ali spojine, ki zanimajo.

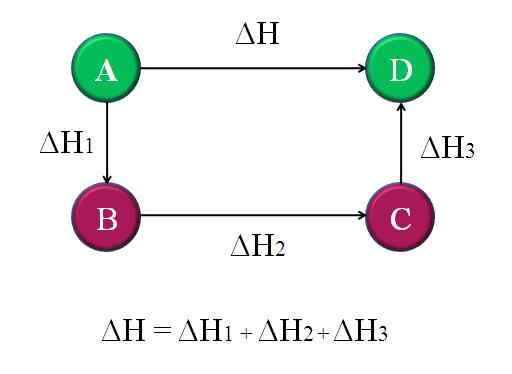
Preprost in splošen diagram, kjer se uporablja zakon Hess za štiri kemijske reakcije. Vir: Gabriel Bolívar.

Na ta način je mogoče izračunati "neznani" ΔH reakcije. Na primer, zgornji diagram pomaga razumeti to idejo. Obstajajo štiri reakcije: A-D, A-B, B-C in C-D. Reakcija A-D je tista, ki ima največji ΔH, ker se tako rekoč pojavljajo, najbolj razvpita kemične spremembe.

Druge reakcije imajo manjše ΔH, saj so sestavljene iz alternativnih korakov ali nadomestnih reakcij, da dosežejo iste produkte d. Zato vsota ΔH₁, ΔH₂ in ΔH₃, Enako bo ΔH. Če to poznate, je mogoče izračunati ΔH ali katero koli drugo entalpijo z uporabo preprostih jaslic. To je Hessov zakon.

Hessov zakon je zelo koristen pri izračunu reakcijskih entalpij, pa tudi entalpije za različne spojine ali nestabilne posrednike.

[TOC]

Pojasnilo Hessovega zakona

Izračun entalpije reakcije

Razlog, zakaj se izpolni:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

To je zato, ker je entalpija ali sprememba entalpije stavna funkcija. To pomeni, da njihove vrednosti niso spremenjene s številom korakov, stopenj ali posrednikov. Na primer, ΔH bo ostal enak, tudi če obstaja ΔH₁₀ to je treba upoštevati v algebrski vsoti.

Entalpije bi lahko vizualizirali kot vrhovi nekaterih gora. Ne glede na to, kako so usmerjeni koraki do njih, višina, ki jih loči od ravni MAR. In natančno je višine, ki se dodajo ali odštejejo za določitev neznane višine okoliške gore.

Vrnitev na prejšnji diagram: a, to je gora, druge gore ipd. Razlika v višini med A in D vrhovi je največja. Če dodate višine med A-B, B-C in C-D, bo dalo enako višini A-D. To je tisto, kar se naredi z entalpijami njihovih kemijskih reakcij.

Vam lahko služi: fosfatna skupina

Entalpija reakcije iz entalpije formacij

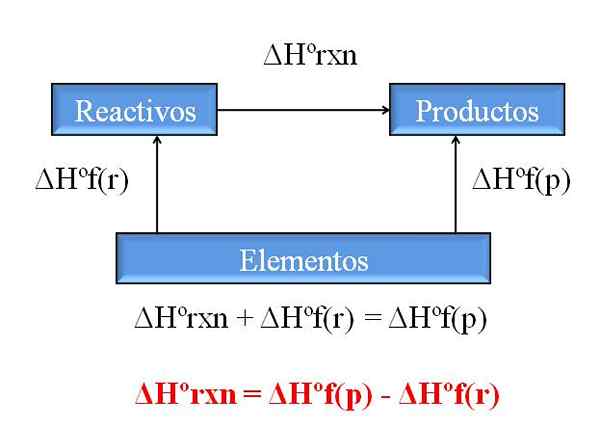Splošni diagram za izračun entalpije reakcije iz entalpije formacij. Vir: Gabriel Bolívar.

Ena najdragocenejših posledic Hessovega zakona je, da omogoča določanje entalpij kakršne koli kemijske reakcije, pri čemer vzame entalpije vseh spojin (reagentov in izdelkov).

Vrhunska slika ponazarja to točko. Razumemo z entalpijo povezane nastajanja toplote, ko se iz njenih elementov oblikuje spojina. Ta entalpija bi postala največja možna razlika med reagenti in izdelki, ne da bi se morali posvetovati z drugimi kemičnimi reakcijami; Vsaj zunaj ločenega treninga spojin.

Kako tokrat preberete diagram? Trik je vedno dodati entalpije, ko gre v smeri puščice, in jih odštejte, ko je puščica na nasprotni poti. Tako ΔHºrxn, standardna reakcijska entalpija, dodaja ΔHºF (reagenti), standardno entalpijo tvorbe reagentov in jih odštejemo ΔHºF (izdelki), standardna entalpija tvorbe izdelkov izdelkov.

Reakcije vsote

Diagrami lahko postanejo zelo zapleteni za razlago, še posebej, kadar je veliko reakcij, ki jih je treba upoštevati. Zato se uporablja vsota reakcij. Ta metoda močno olajša izračun entalpij in pospeši razumevanje Hessovega zakona.

Recimo na primer, da želite določiti ΔHºrxn naslednje reakcije:

A + B + C → ABC

In imamo tudi še dve reakciji:

A + B → AB (ΔHº₁)

AB + C → ABC (ΔHº₂)

Zanimivo je, da so A + B + C na levi strani (reagenti) in da je ABC na desni strani (izdelki). Nato preprosto nadaljujemo z dodajanjem zadnjih dveh reakcij:

A + B → AB

AB + C → ABC

A + AB + C → ABC + AB

Ker je AB z obeh strani, je odpravljen. In tako imamo:

A + B + C → ABC

ΔHºrxn = ΔHº₁ + ΔHº₂

Če dodate reakcije, je uporaba katerega koli diagrama izpuščena.

Prijave Hessovega zakona

Hessov zakon omogoča, da brez potrebe po poskusih, entalpijah za različne kemijske reakcije ali pojave. Nekateri od njih so navedeni:

- Usposabljanje entalpije za nestabilne spojine ali posrednike, kot jih običajno imamo v organski kemiji.

-Entalpije faznih prehodov v preučevanju kristalnih trdnih snovi.

Vam lahko služi: kemična spojina

-Entalpije alotropnih prehodov, kot sta tista med grafitom in diamantom.

Prav tako se Hessov zakon uporablja za določanje retikularne energije trdne snovi in ​​elektronskih afinitet nekaterih atomov.

Primeri: rešene vaje

- Primer 1

Izračunajte ΔHRXN naslednje reakcije:

2HCl (g) + f₂(g) → 2HF (L) + Cl₂(g)

Če imate naslednje reakcije in njihove entalpije:

4HCl (g) + oz₂(g) → 2H₂Ali (l) + 2cl₂(g) (ΔH = -202.4 kJ/mol)

1/2H₂(g) + 1/2f₂(g) → hf (l) (ΔH = -600.0 kJ/mol)

H₂(g) + 1/2o₂(g) → h₂Ali (l) (ΔH = -285.8 kJ/mol)

Naročanje enačb

Za začetek moramo dodati reakcije tako, da HCl in F₂ so na levi strani, HF in Cl₂, Na desni strani. Toda še pomembneje je, da opazimo, da toliko h₂ kot h₂Ali niso v enačbi obresti. Zato jih moramo preklicati v znesku in narediti, da stehiometrični koeficienti sovpadajo z množenjem:

2HCl (g) + 1/2₂(g) → h₂Ali (l) + cl₂(g) (ΔH = -202.4 kJ/mol) * (1/2)

Ta enačba je bila pomnožena z 1/2, da bi imela 2HCl namesto 4HCl

H₂(g) + f₂(g) → 2HF (l) (ΔH = -600.0 kJ/mol) * (2)

Ta enačba se je pomnožila z 2, da ima F₂ in ne 1/2f₂

H₂Ali (l) → h₂(g) + 1/2o₂(g) (ΔH = -285.8 kJ/mol) * (-1)

Medtem se je slednji pomnožil z -1, da bi ga "obrnil". Tako imamo urejene enačbe in pripravljeni dodati.

Vsota enačb

Če dodamo vse, nam daje:

2HCl (g) + 1/2₂(g) → h₂Ali (l) + cl₂(g) (ΔH = -101.2 kJ/mol)

H₂(g) + f₂(g) → 2HF (L) ΔH = -1200.0 kJ/mol)

H₂Ali (l) → h₂(g) + 1/2o₂(g) (ΔH = 285.8 kJ/mol)

2HCl (g) + f₂(g) → 2HF (L) +Cl₂(g)

Upoštevajte, da pogoji 1/2₂, H₂Ali in h₂ Odpovedani so, ker so na obeh straneh puščice. Dodane so tudi entalpije, ki dajejo:

ΔHRX = 285.8 kJ/mol + (-101.2 kJ/mol) + (-1200.0 kJ/mol)

Ta izraz je enak začetku:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

In tako imamo, da je ΔHRX enak:

ΔHRX = -1015.4 kJ/mol

- Primer 2

V tem primeru bo razvidno, da entalpije nadomestnih reakcij ustrezajo entalpijam tvorbe interesnih spojin.

Za naslednjo reakcijo razgradnje je želeti določiti ΔHRXN:

2SO₃(g) → 2SO₂(g) + oz₂(g)

In trening entalpije SO spojin se šteje na roki₃ In tako₂:

S (s) + o₂(g) → Torej₂(g) (ΔH = -296.8 kJ/mol)

Vam lahko služi: izopreno: struktura, lastnosti, aplikacije

S (s) + 3/2o₂(g) → Torej₃(g) (ΔH = -395.6 kJ/mol)

Naročanje enačb

Ta vaja bo rešena na enak način kot prejšnji primer. To bi moralo biti tako₃ biti prav in pomnožite z 2. Za to moramo "obrniti" enačbo formacije SO₃ Pomnožimo ga za -1 in nato pomnožimo z 2:

2SO₃(g) → 2s (s) + 3o₂(g) (ΔH = -395.6 kJ/mol) * (-2)

Enačba tvorbe SO₂ Pomnožimo ga tudi z 2:

2s (s) + 2₂(g) → 2SO₂(g) (ΔH = -296.8 kJ/mol) * (2)

Vsota enačb

Zdaj so dodane enačbe:

2SO₃(g) → 2s (s) + 3o₂(g) (ΔH = 791.2 kJ/mol)

2s (s) + 2₂(g) → 2SO₂(g) (ΔH = -593.6 kJ/mol)

2SO₃(g) → 2SO₂(g) + oz₂(g)

Upoštevajte, da je izraz 2s odpravljen, ker je na obeh straneh puščice. Tudi 3₂ 2o se odšteje₂ dati o₂. Vsota entalpij in zato bo vrednost ΔHRXN:

ΔH = ΔHrxn = 791.2 kJ/mol + (-593.6 kJ/mol)

= 197.6 kJ/mol

Kot vsaka reakcija razgradnje je tudi endotermična, zato je njegova entalpija pozitivna.

Alternativna metoda

Obstaja metoda, s katero lahko dosežemo ta isti rezultat na bolj neposreden in preprost način. To je bilo omenjeno v prejšnjem razdelku.

2SO₃(g) → 2SO₂(g) + oz₂(g)

Za določitev ΔHRXN te reakcije moramo izračunati ΔHºF (reagenti) in ΔHºF (produkti). ΔHºF (tako₃) je enak -395.6 kJ/mol, medtem ko je ΔHºF (tako₂) je enak -296.8 kJ/mol. ΔHºF (ali₂) je enak 0, saj elementarni kisik obstaja kot molekula O₂ in ne kot atomi ali prosti.

Torej, imamo:

ΔHRXN = ΔHºF (izdelki) - ΔHºF (reagenti)

= [ΔHºF (torej₂) + ΔHºF (ali₂)] - ΔHºF (tako₃)

= ΔHºF (torej₂) - ΔHºF (tako₃)

Vendar moramo pomnožiti obe entalpiji za 2, da se ujemamo s stehiometričnimi koeficienti glede na kemijsko enačbo:

ΔHrxn = 2ΔHºf (tako₂) - 2ΔHºF (tako₃)

In izračunavamo:

ΔHrxn = 2 (-296.8 kJ/mol) - 2 (-395.6 kJ/mol)

= 197.6 kJ/mol

Pravzaprav je to tako, kot je običajno raje razrešiti vse vaje, v katerih se uporablja zakon o HESS.

Reference

1. Whitten, Davis, Peck & Stanley. (2008). Kemija. (8. izd.). Cengage učenje.
2. Wikipedija. (2020). Hessov zakon. Pridobljeno iz: v.Wikipedija.org
3. Cohen Shelly. (18. maja 2020). Hessov zakon. Kemija librettexts. Okrevano od: kem.Librettexts.org
4. Clark Jim. (2010). Hessovi izračuni sprememb in entalpije. Okrevano od: Chemguide.co.Združeno kraljestvo
5. Čelada, Anne Marie, ph.D. (11. februar 2020). Hessova zakonska definicija. Okreval od: Thoughtco.com
6. Foist Laura. (2020). Hessov zakon: definicija, formula in primer. Študij. Okrevano od: študij.com
7. Quimitube. (2014). Teorija 14 Termokemija: Izračun entalpije reakcije Hessovega zakona. Okreval od: quimitube.com