Zakon o Gaussu

Pojasnjujemo, kaj je Gaussov zakon, njene aplikacije in postavimo rešene vaje

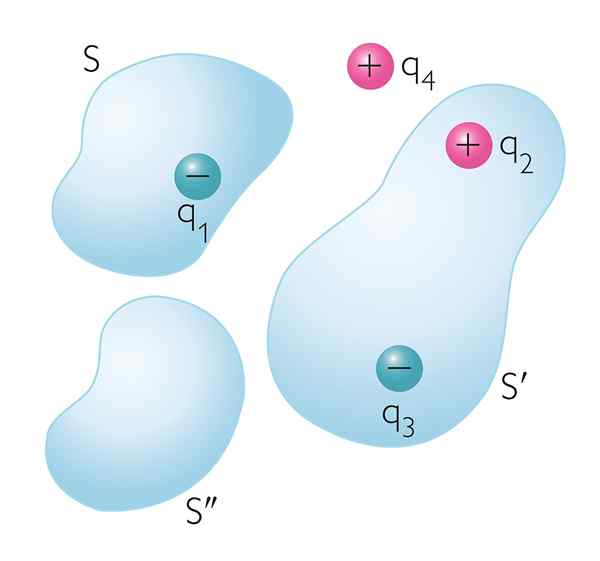
Slika 1. Električni naboji znotraj in zunaj Gaussovih površin poljubno. Samo obremenitve, zaklenjene znotraj vsake površine, prispevajo k neto električnem toku skozi njih

Kaj je Gaussov zakon?

The Zakon o Gaussu navaja, da je pretok električnega polja skozi namišljeno zaprto površino sorazmerno z neto vrednostjo obremenitve delcev, ki jih najdemo znotraj omenjene površine.

Označevanje električnega toka skozi zaprto površino, kot je Φ_In in neto obremenitev, ki jo površina zaklene Q_ENF, Potem je vzpostavljen naslednji matematični odnos:

Φ_In = C ∙ Q_ENF

Kje c To je konstanta sorazmernosti.

Pojasnilo Gaussovega zakona

Da bi razumeli pomen Gaussovega zakona.

Električni naboj

Električni naboj je ena temeljnih lastnosti snovi. Naložen predmet ima lahko eno od dveh vrst obremenitve: pozitiven ali negativen, čeprav so običajno predmeti nevtralni, to je, da imajo enako količino negativne obremenitve kot pozitivno.

Dva predmeta, naložena z nalaganjem iste vrste. Nasprotno, ko ima vsaka telesa veliko različnih znakov, potem privlačijo. Ta vrsta interakcije na daljavo je znana kot električna interakcija.

V mednarodnem sistemu enot, če se električni naboj meri v Culumbios (C). Negativni osnovni nosilec tovora je elektron Z obremenitvijo -1,6 x 10^-19C In pozitiven osnovni nosilec obremenitve je proton z vrednostjo obremenitve +1,6 x 10^-19C. Običajno naložena telesa imajo med 10^-9C in 10^-3C.

električno polje

Električno obremenjeno telo spremeni prostor v svoji okolici in ga napolni z nečim nevidnim, imenovanim električno polje. Če želite vedeti, da je to polje prisotno, je potrebna posebna testna obremenitev.

Vam lahko služi: preprosto harmonično gibanje

Če je preskusna obremenitev nameščena na mestu, kjer je električno polje, se v določeni smeri pojavi sila, ki je enaka kot pri električnem polju. Intenzivnost polja je sila na preskusni obremenitvi, deljeno s količino obremenitve istega. Nato električne poljske enote In V mednarodnem sistemu enot so Newton med Coulomb: [E] = n/c.

Pozitivne specifične obremenitve proizvajajo radialno polje zunaj, medtem ko negativne obremenitve proizvajajo radialno usmerjeno polje navznoter. Poleg tega polje, ki ga povzroča točno breme, razpada z obratnim kvadratom razdalje do omenjene obremenitve.

Električne poljske linije

Michael Faraday (1791 - 1867) je bil prvi, ki je imel miselno podobo električnega polja in si ga predstavljal kot črte, ki sledijo smeri polja. V primeru pozitivne natančne obremenitve so te črte radialne, začenši od središča. Kjer so črte bolj skupaj, je polje bolj intenzivno in manj intenzivno tam, kjer so bolj ločene.

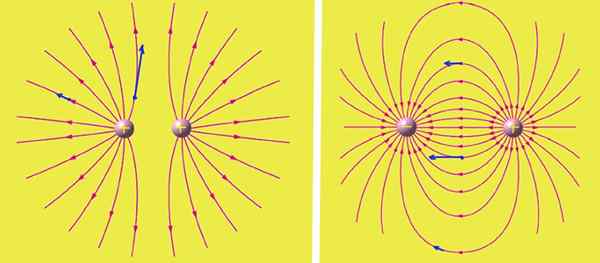Slika 2. Na levih poljskih črtah dveh enakih in pozitivnih nabojev. Na desni strani obremenitvenih poljskih črt enake velikosti, vendar nasprotni znaki. Modre puščice predstavljajo vektor električnega polja v različnih položajih. Vir: Wikimedia Commons.

Pozitivne obremenitve so viri, od koder se pojavljajo električne poljske črte, negativne obremenitve.

Električne poljske linije se ne zapirajo na sebe. V naboru obremenitev črte pustijo pozitivne naboje in vstopijo v pozitivne, lahko pa tudi pridejo ali pridejo iz neskončnosti.

Vam lahko služi: stabilno ravnovesje: koncept in primeri

Prav tako se sekajo in na vsaki točki v prostoru je vektor električnega polja tangenten na poljsko črto in sorazmerno z gostoto črte.

Slika 3. Deklica je električno zaračunana, da je v stiku s kupolo generatorja Van der Graaf. Vaši lasje sledijo črtam električnega polja. Vir: Wikimedia Commons.

Pretok električnega polja

Električne poljske črte spominjajo na trenutne črte reke, ki nežno teče, od tu se rodi koncept pretoka električnega polja.

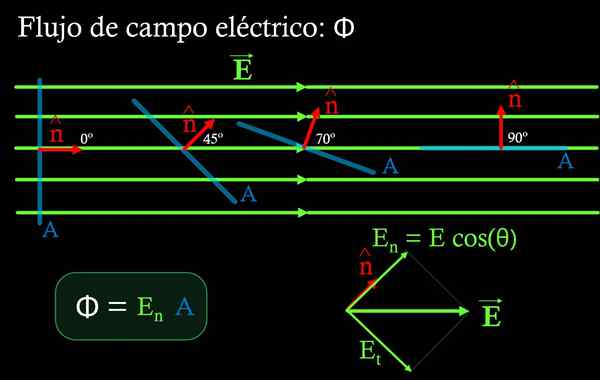Slika 4. Električno polje teče skozi površino območja A je odvisno od kota, ki nastane med omenjeno površino in poljem in. Največji pretok dobimo, ko je površina pravokotna na polje in je pretok enaka, ko je površina vzporedna s poljem. Vir: f. Zapata.

V regiji, kjer je električno polje enakomerno, je tok φ skozi ravno površino produkt običajne komponente E_n na omenjeno površino, pomnoženo na območju Do Istega:

Φ = e_n ∙ a

Komponenta e_n Dobimo ga tako, da pomnožimo velikost električnega polja s kosinusom kota, ki se tvori med poljem in normalnim enotnim vektorjem na površino območja Do. (Glej sliko 4).

Prijave za pravo Gauss

Gaussov zakon je mogoče uporabiti za določitev električnega polja, ki ga proizvajajo porazdelitve obremenitve z visoko stopnjo simetrije.

Električno polje natančnega bremena

Točna obremenitev ustvari radialno električno polje, ki je odhodno, če je obremenitev pozitivna in dohodna drugače.

Izbira kot Gaussova površina namišljena sfera radia R in koncentrična do obremenitve Q, na vseh točkah površine omenjene sfere je električno polje enakovredno, njegova smer pa je vedno normalna na površino. Nato je v tem primeru pretok električnega polja rezultat obsega polja s skupno površino sferične površine:

Lahko vam služi: Mehanika tekočine: zgodovina, kakšne študije, osnove

Φ = e ∙ a = e ∙ 4πr²

Po drugi strani Gaussov zakon ugotovi, da: φ = c ∙ Q, ki je konstanta sorazmernosti c. Pri delu v enotah sistema mednarodnih ukrepov, konstanta c To je obratno od dodatka vakuuma, Gaussov zakon pa je oblikovan na naslednji način:

Φ = (1/ε_tudi) ∙ q

Vključitev rezultata, pridobljenega za pretok zakona Gauss, je:

E ∙ 4πr² = (1/ε_tudi) ∙ q

In za velikost In rezultat:

E = (1/4πε_tudi) ∙ (q/ r²)

V celoti sovpada s Coulomb zakonom električnega polja točnega bremena.

Vaje

Vaja 1

Dve posebni naboji najdemo znotraj poljubne Gaussove površine. Znano je, da ima eden od njih vrednost +3 NC (3 nano-Coulomb). Če je mrežno električno polje skozi Gaussovo površino 113 (n/c) m², Kakšna bo vrednost druge obremenitve?

Rešitev

Gaussov zakon to ugotovi

Φ_In = (1/ε_tudi) ∙ q_ENF

Od tam je neto obremenitev zaklenjena:

Q_ENF = Φ_In ∙ ε_tudi

Zamenjava rezultatov podatkov:

Q_ENF = 113 (n/c) m² ∙ 8,85 x 10^-12 (C² m^-2 N^-1) = 1 x 10^-9 C = 1 nc.

Ampak Q_ENF = +Q - Q, Kadar ima pozitivna obremenitev znano vrednost +3 NC, bo obremenitev nujno -2 nc.

Vaja 2

Na sliki 2 je razporeditev (na levi) dveh pozitivnih nabojev, vsaka z vrednostjo +Q in drugo ureditev (desno) z eno obremenitvijo +Q in drugi -Q. Vsaka razporeditev je zaklenjena v namišljeni škatli z vsemi 10 cm robov. Da | q | = 3 μC, poiščite neto električno polje skozi škatlo za vsako ureditev.

Rešitev

V prvi ureditvi je neto tok:

Φ_In = (1/ε_tudi) ∙ ( + q + q) = 678000 (n/c) m²

V desni razporedi je neto tok skozi namišljeno polje, ki vsebuje navor obremenitev.

Reference

1. Cosenza, m. Elektromagnetizem. Univerza v Andih.
2. Díaz, r. Elektrodinamika: zapiske razredov. Nacionalna univerza v Kolumbiji.
3. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 6. Elektromagnetizem. Uredil Douglas Figueroa (USB).
4. Jackson, J. D. Klasična elektrodinamika. 3. mesto. Ed. Wiley.
5. Tarazona, c. Uvod v elektrodinamiko. Uredniška univerza Manuela Beltrán.