Fizično

Faraday Formul Law, enote, poskusi, vadba,

Faraday Formul Law, enote, poskusi, vadba,

The Faraday zakon V elektromagnetizmu ugotovi, da lahko spreminjajoči se pretok magnetnega polja v zaprtem vezju sproži električni tok.

Leta 1831 je angleški fizik Michael Faraday doživel premikajoče se voznike znotraj magnetnega polja in tudi različna magnetna polja, ki so prečkala fiksne gonilnike.

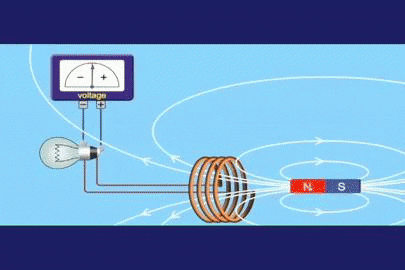Slika 1. Faraday indukcijski eksperiment

Faraday je spoznal, da če bo v času spreminjal pretok magnetnega polja, je lahko vzpostavil napetost, sorazmerno z omenjenimi spremembami. Če je ε inducirana elektromotorna napetost ali sila (inducirana FEM) in φ je pretok magnetnega polja, v matematični obliki se lahko izrazi:

| ε | = Δφ/ΔT

Kadar simbol Δ kaže na spreminjanje količine in palice v FEM, kažejo absolutno vrednost tega. Ker gre za zaprto vezje, lahko tok kroži v eni ali drugi smeri.

Magnetni tok, ki ga proizvaja magnetno polje skozi površino, se lahko na primer razlikuje na različne načine:

-Premikanje paličnega magneta skozi krožno spiralo.

-Povečanje ali zmanjšanje intenzivnosti magnetnega polja, ki prečka zanko.

-Če pustite polje pritrjeno, vendar z nekaterim mehanizmom spremeni območje zanke.

-Združevanje zgornjih metod.

Slika 2. Angleški fizik Michael Faraday (1791-1867).

[TOC]

Formule in enote

Recimo, da obstaja zaprto vezje območja A, na primer krožna spirala ali upor, ki je enak sliki 1, in da obstaja magnet, ki proizvaja magnetno polje B.

Pretok magnetnega polja φ je skalarna količina, ki se nanaša na količino poljskih črt, ki prečkajo območje A. Na sliki 1 so bele črte, ki zapuščajo severni pol magneta in se vrnejo na jugu.

Vam lahko služi: Brayton Cicl: Process, učinkovitost, aplikacije, vaje

Intenzivnost polja bo sorazmerna s številom linij na enoto območja, tako da lahko vidimo, da je na poljah zelo intenziven. Lahko pa imamo zelo intenzivno polje, ki ne proizvaja toka v zanki, kar lahko dosežemo s spreminjanjem orientacije tega (ali magneta).

Če želite upoštevati orientacijski faktor, je pretok magnetnega polja opredeljen kot skalarni izdelek med B in n, biti n Normalni enotni vektor na površino spaze in to kaže na njegovo orientacijo:

Φ = B•n A = ba.cosθ

Kjer je θ kot med B in n. Če na primer B in n So pravokotne, tok magnetnega polja je ničen, ker je v tem primeru polje tangentno na ravnino ločene in ne more prečkati njegove površine.

Namesto tega B in n So vzporedni, to pomeni, da je polje pravokotno na ravnino spira in črte gredo skozi maksimum.

Mednarodna sistemska enota za F je Weber (W), kjer je 1 W = 1 t.m2 (bere "Tesla na kvadratni meter").

Lenz zakon 

Na sliki 1 lahko vidimo, da se polarnost napetosti spreminja, ko se magnet premika. Polarnost določa Lenzov zakon, ki navaja, da mora inducirana napetost nasprotovati variaciji, ki jo proizvaja.

Če se na primer magnetni tok, ki ga proizvaja magnet, poveča, voznik vzpostavi tok, ki kroži v ustvarjanju lastnega toka, ki nasprotuje temu povečanju.

Če se nasprotno, tok, ki ga ustvarja magnet.

Vam lahko služi: termometrične lestvice

Če želite upoštevati ta pojav, je negativni znak za Faradayev zakon postavljen prej in ni več treba namestiti palic absolutne vrednosti:

ε = -Δφ/ΔT

To je zakon Faraday-Lenza. Če je variacija pretoka neskončno majhna, se delte nadomestijo z diferenciali:

ε = -dφ/dt

Prejšnja enačba velja za zanko. Če pa imamo vrtečo se tuljavo, je rezultat veliko boljši, saj FEM pomnoži v krat:

ε = - n (dφ/dt)

Faraday Eksperimenti

Za izdelavo toka, ki prižge žarnico, med magnetom in spiralo mora biti relativno gibanje. To je eden od načinov, kako se lahko tok razlikuje, saj na ta način intenzivnost polja, ki prečka zanko, spremeni.

V trenutku, ko se gibanje magneta preneha, žarnica ugasne, tudi če magnet še vedno ostane v ločitvi. Kar je potrebno za kroženje toka do žarnice.

Ko se magnetno polje sčasoma razlikuje, ga lahko izrazimo kot:

B = B (T).

Z ohranjanjem konstantne površine in ga pritrjeno pod konstantnim kotom, ki je v primeru slike 0 °, nato:

 Za zanko slike 1 (cos 0º = 1):

Razbijanje spremenljivih površin

Če lahko spremenite območje spaze, pri čemer pustite njegovo orientacijo pritrditev in jo postavite na sredino stalnega polja, je inducirani FEM podan z:

Eden od načinov za to je, da z določeno hitrostjo postavite palico, ki drsi na prevodni tirnici, kot je prikazano na naslednji sliki.

Vam lahko služi: ío (satelit) Slika 3. Drsni generator. Vir: Serway, r. Fizika za znanost in inženiring.

Bar in tirnica ter žarnica ali upor, povezana z žico gonilnika, tvorita zaprto vezje v obliki pravokotnega lopata.

Ko drsimo palico, dolžina x povečuje ali se zmanjšuje, s tem pa se območje sprememb zanke, kar je dovolj za ustvarjanje spremenljivega toka.

Sprememba magnetnega toka z vrtenjem

Kot smo že povedali, če je kot med B In normalna zanka je raznolika, pretok polja se spremeni v skladu z:

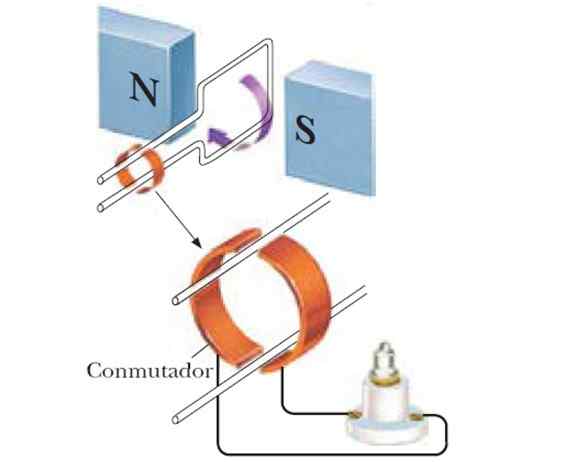Slika 4. Če se zanka vrti med drogovi magneta, dobimo sinusoidni generator. Vir: f. Zapata.

Tako dobimo sinusoidni generator, in če se uporablja eno število tuljav, je inducirana FEM večja:

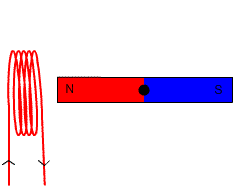Slika 5. V tem generatorju se magnet zasuka, da sproži tok v tuljavi. Vir: Wikimedia Commons.

Vaja rešena

Krožna tuljava n krogov in radia R, kotno zavije ω na sredini magnetnega polja magnitude B. Poiščite izraz za največjo inducirano FEM v tuljavi.

Rešitev

Izraz za FEM, ki ga povzroča vrtenje, se uporablja, ko ima tuljava N kroži, vedoč, da:

-Območje tuljave je a = πr2

-Kot θ se spreminja glede na čas kot θ = ωt

Pomembno je upoštevati, da je θ = ωt najprej zamenjan v Faradayjevem zakonu in nato Izhaja od časa:

ε = -nba (cos θ) '= -nb (πr2).[cos (ωt)] '= nbω (πr2) Sen (ωt)

Ker se zahteva največji FEM, se to zgodi vsakič, ko je Sen ωt = 1, tako končno:

εMax = Nbω (πr2)

Reference

  1. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 6. Elektromagnetizem. Uredil Douglas Figueroa (USB).
  2. Giambattista, a. 2010. Fizika. Druga izdaja. McGraw Hill.
  3. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed. Dvorana Prentice.
  4. Resnick, r. 1999. Fizično. Vol. 2. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
  5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 2.