Značilnosti, vrste in vadbene konvergentne značilnosti leče

The Konvergentne leče So tisti, ki so debelejši v osrednjem in tanjšem delu na robovih. Posledično se v eni točki koncentrirajo (zbližajo) svetlobni žarki, ki vplivajo vzporedno z glavno osjo. Ta točka se imenuje fokus ali fokus slike in je predstavljena s črko F. Konvergentne ali pozitivne leče tvorijo tako imenovane resnične slike predmetov.

Tipičen primer konvergentnega leče je povečevalno steklo. Vendar je običajno najti to vrsto leč na veliko bolj zapletenih napravah, kot so mikroskopi ali teleskopi. Pravzaprav je osnovni sestavljeni mikroskop, ki ga sestavljata dve konvergentni leči, ki imata majhno goriščno razdaljo. Te leče se imenujejo tarča in očesni.

Povečevalna stekla, konvergentna leča. 

Konvergentne leče se uporabljajo v optiki za različne aplikacije, čeprav je morda najbolj znana popravljanje napak. Tako so navedeni, da se ukvarjajo.

[TOC]

Značilnosti

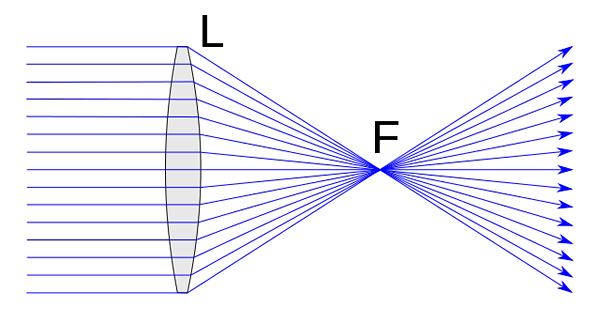Konvergentna leča. Chetvrno [CC0]

Konvergentne leče imajo serijske funkcije, ki jih definirajo. Vsekakor je morda najpomembnejše tisto, kar smo že napredovali v njegovi definiciji. Tako je za konvergentne leče značilno, da se skozi fokus preusmeri vsak žarek, ki vpliva nanje v smeri, vzporedno z glavno osi.

Poleg tega je na vzajemno način vsak incidentni žarek, ki prehaja fokus.

Elementi konvergentnih leč

Ob svoji študiji je pomembno vedeti, kakšni elementi so leče na splošno in konvergentne leče.

Na splošno se imenuje optično središče leče do točke, s katerim vsak žarek, ki gre skozi njega, ne doživi nobenega odstopanja.

Glavna os je črta, ki se pridruži optičnemu centru in glavnem fokusu, ki smo jo že komentirali, ki je predstavljena s črko F.

Vam lahko služi: tono: rešene transformacije, enakovrednosti in vaje

Glavni poudarek se imenuje do točke, ko najdejo vsi žarki, ki vplivajo na objektiv vzporedno z glavno osi.

Razdalja med optičnim centrom in fokusom se imenuje žariščna razdalja.

Središča ukrivljenosti so opredeljena kot središča sfer, ki ustvarjajo lečo; Po drugi strani pa radijski sprejemniki ukrivljenosti radijskih sprejemnikov sfer, ki povzročajo lečo.

In končno se imenuje optična ravnina do osrednje ravnine leče.

Nastajanje slik v konvergentnih lečah

Ob nastanku slik v konvergentnih lečah je treba upoštevati niz osnovnih pravil, ki so razložena spodaj.

Če žarek vzporedno vpliva na lečo, se nastajajoči žarek zbliža. Obratno, če vpadni žarek prestopi objekt osredotočenost, se strela pojavi v smeri, vzporedno z osi. Končno se žarki, ki prečkajo optično središče.

Posledično lahko v konvergentnem objektivu podate naslednje situacije:

- Da je predmet nameščen glede na optično ravnino na daljavo, večjo od dvojne goriščne razdalje. V tem primeru je slika, ki se pojavi, resnična, obrnjena in manjša od predmeta.

- Da je predmet nameščen na razdalji od optične ravnine, ki je enaka dvakratni goriščni razdalji. Ko se to zgodi, je pridobljena slika resnična, obrnjena slika in enake velikosti kot objekt.

- Da je predmet na razdalji od optične ravnine med enkrat in dvakratno goriščno razdaljo. Torej je nastala slika resnična, obrnjena in večja od prvotnega predmeta.

- Da je predmet nameščen na razdalji od optične ravnine nižje od goriščne razdalje. V tem primeru bo slika navidezna, neposredna in večja od predmeta.

Vam lahko služi: magnetni šok: enote, formule, izračun, primeri

Vrste konvergentne leče

Obstajajo tri različne vrste konvergentnih leč: bikonveksne leče, planokonveksne leče in konkavokonveksne leče.

Bikonveksne leče, kot že ime pove, sestavljajo dve konveksni površini. Plonconvexas imajo medtem ravno površino in drugo izbočeno. In končno, konkavokonveksne leče sestavljajo rahlo konkavna površina in druga izbočena.

Razlika z divergentnimi lečami

Konvergentna leča. Fir0002 (pogovor) (nalaganje) [cc by-sa 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Divergentne leče se na drugi strani razlikujejo od konvergentnega po tem, da se debelina zmanjšuje od robov proti sredini. Tako v nasprotju s tistim, kar se je zgodilo s konvergentom, v tej vrsti leč žarki svetlobe, ki vzporedno vplivajo na glavno osi. Na ta način tvorijo tako imenovano virtualne slike predmetov.

V optiki se za popravljanje miopije večinoma uporabljajo divergentne ali negativne leče, kot so znane tudi v glavnem.

Gaussove enačbe tankih leč in povečane leče

Na splošno so vrsta leč, ki jih preučujemo. Ti so opredeljeni kot tisti, ki imajo majhno debelino v primerjavi z ukrivljenostjo površin, ki jih omejujejo.

To vrsto leče je mogoče preučiti z Gaussovo enačbo in z enačbo, ki omogoča določitev povečanja leče.

Gaussova enačba

Gaussova enačba tankih leč služi za reševanje množice osnovnih težav z optiko. Zato je velik pomen. Vaš izraz je naslednji:

1/f = 1/p +1/q

Kjer je 1/ f tisto, kar se imenuje moč leče in F je goriščna razdalja ali oddaljenost od optičnega središča do focusa. Enota mere moči leče je diopter (d), ki je 1 d = 1 m^-1. P in Q sta P in Q razdalja, na kateri je predmet in razdalja, na kateri je njegova slika.

Lahko vam služi: Teorija velikega poka: značilnosti, stopnje, dokazi, problemi

Povečana leča

Bočno povečanje tanke leče dobimo z naslednjim izrazom:

M = - Q / P

Kjer je m povečanje. Iz vrednosti povečanja je mogoče sklepati vrsto posledic:

DA | M | > 1, velikost slike je večja od velikosti predmeta

DA | M | < 1, el tamaño de la imagen es menor que el del objeto

Če je m> 0, je slika prava in na isti strani leče kot objekt (virtualna slika)

Da m < 0, la imagen está invertida y en el lado contrario que el objeto (imagen real)

Vaja rešena

Telo se nahaja meter stran od konvergentne leče, ki ima goriščno razdaljo 0, 5 metrov. Kakšna bo podoba telesa? Kako daleč boste našli?

Imamo naslednje podatke: p = 1 m; F = 0,5 m.

Te vrednosti nadomestimo v Gaussovi enačbi tankih leč:

1/f = 1/p +1/q

In ostane naslednje:

1/0,5 = 1 + 1/q; 2 = 1 + 1/q

Očistimo 1/Q

1/q = 1

Nato očistiti Q in pridobiti:

Q = 1

Od tam nadomestimo v enačbi povečanja leče:

M = -q / p = -1 / 1 = -1

Zato je slika resnična že od q> 0, obrnjena, ker m < 0 y de igual tamaño dado que el valor absoluto de M es 1. Por último, la imagen se encuentra a un metro de distancia del foco.

Reference

1. Svetloba (n.d.). V Wikipediji. Pridobljeno 18. marca 2019 iz tega.Wikipedija.org.
2. Lekner, John (1987). Teorija razmišljanja, elektromagnetnih in delnih valov. Springer.
3. Svetloba (n.d.). V Wikipediji. Pridobljeno 20. marca 2019, od.Wikipedija.org.
4. Leča (n.d.). V Wikipediji. Pridobljeno 17. marca 2019 iz tega.Wikipedija.org.
5. Objektiv (optika). V Wikipediji. Pridobljeno 19. marca 2019, od.Wikipedija.org.
6. ACTS, Eugene (2002). Optika (4. izd.). Addison Wesley.
7. Tupler, Paul Allen (1994). Fizično. 3. izdaja. Barcelona: Obrnil sem se.