Magnetne indukcijske formule, kako se izračuna in primeri

The magnetna indukcija ali gostota magnetnega toka je sprememba okolja, ki ga povzroča prisotnost električnih tokov. Spreminjajo naravo okoliškega prostora in ustvarjajo a Polje Vektor.

Vektor Magnetna indukcija, gostota magnetnega toka Ali preprosto magnetno polje B, Ima tri značilne značilnosti: intenzivnost, izražena s številčno vrednostjo, naslovom in tudi občutkom, ki je naveden na vsaki točki v vesolju. Poudarjeno je krepko, da ga ločimo od čisto številčnih količin ali skalarnih.

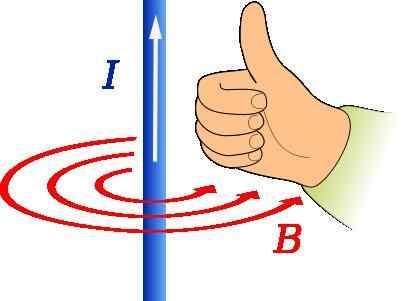
Pravilo desnega palca za določitev smeri in smer magnetne indukcijske vektorja. Vir: jfmelero [cc by-sa 4.0 (https: // creativeCommons.Org/licence/by-sa/4.0)]

Pravilo desnega palca se uporablja za iskanje smeri in smeri magnetnega polja, ki izvira iz žice, ki prevaža tok, kot je prikazano na zgornji sliki.

Palec desne roke naj usmeri v smeri toka. Potem obrat preostalih prstov kaže na obliko B, da na sliki predstavljajo koncentrični krogi rdeče barve.

V tem primeru naslov B Je tangencialen za koncentrični obod z žico in pomen je v nasprotju z rokami ure.

The magnetna indukcija B V mednarodnem sistemu se meri tesla (t), vendar je bolj pogosto meriti v drugi enoti, imenovani Gauss (G). Obe enoti sta bili imenovani v čast Nikole Tesla (1856-1943) in Carla Friedricha Gaussa (1777-1855) za njihov izjemen prispevek k znanosti o električni energiji in magnetizmu.

[TOC]

Katere so lastnosti magnetne indukcije ali gostote magnetnega toka?

Kompas, ki je postavljen v bližini žice s tokom, se bo vedno poravnal z B. Danski fizik Hans Christian Oersted (1777-1851) je bil prvi, ki je ta pojav uresničil na začetku 19. stoletja.

Lahko vam služi: Areolar Hitrost: kako se izračuna in reši vaje

In ko tok preneha, kompas kaže na geografski sever, kot vedno. S skrbnim spreminjanjem položaja kompasa dobimo zemljevid iz oblike magnetnega polja.

Ta zemljevid ima vedno obliko koncentričnih krogov do žice, kot je opisano na začetku. Na ta način ga je mogoče vizualizirati B.

Tudi če žica ni ravna, vektor B bo tvoril koncentrične kroge okoli njega. Če želite določiti, kakšna oblika ima polje, je dovolj, da si predstavljamo zelo majhne žične segmente, tako majhne, ​​da se zdijo pravokotni in obkroženi s koncentričnimi okoliščinami.

Magnetne poljske črte, ki jih proizvaja žična zanka, ki prevaža tok. Vir: Pixabay.com

To kaže na pomembno lastnost linij magnetnega polja B: Nimajo načela ali konca, vedno so zaprte krivulje.

Zakon o Biot-Savart

Devetnajsto stoletje je določilo začetek dobe električne energije in magnetizma v znanosti. V bližini leta 1820 francoski fiziki Jean Marie Biot (1774-1862) in Felix Savart (1791-1841) sta odkrila zakon, ki nosi njegovo ime in ki omogoča izračun vektorja B.

Naslednja opažanja so prispevali o prispevku k magnetnemu polju, ki ga proizvede diferencialni segment žice dl ki prevaža električni tok Yo:

• Velikost B zmanjšuje s obratnim kvadratom razdalje do žice (to je smiselno: daleč od žice B Mora biti manj kot v bližnjih točkah).
• Velikost B Sorazmerna z intenzivnostjo toka Yo ki potuje na žico.
• Naslov B To je tangencialno za obseg radia r osredotočena na žico in smer B Kot smo rekli, je dana s pravim pravilom palca.

Vektorski ali izdelka za navzkrižno izdelek je primerno matematično orodje za izražanje zadnje točke. Za vzpostavitev vektorskega izdelka sta potrebna dva vektorja, ki sta opredeljena na naslednji način:

• dl Je vektor, katerega velikost je dolžina diferencialnega segmenta dl
• r To je vektor, ki sega od žice do točke, ko želite najti polje

Vam lahko služi: elektromagnetni spekter: značilnosti, pasovi, aplikacije

Formule

Vse to je mogoče kombinirati v matematičnem izrazu:

Konstanta sorazmernosti, potrebna za določitev enakosti Magnetna prepustnost prostega prostora μ_tudi  = 4π.10^-7 T.m/a

Ta izraz je Biot in Savart zakon, ki omogoča izračun magnetnega polja trenutnega segmenta.

Takšen segment mora biti del večjega in večjega vezja: trenutna porazdelitev.

Pogoj, da je vezje zaprto, je potreben, da se električni tok pretaka. Električni tok ne more teči v odprtih vezjih.

Končno, za iskanje skupnega magnetnega polja te trenutne porazdelitve, se dodajo vsi prispevki vsakega diferencialnega segmenta dl. To je enakovredno integraciji vso distribucijo:

Za uporabo zakona o Biot-Savart in izračun magnetnega indukcijskega vektorja je treba upoštevati zelo pomembne pomembne točke:

• Vektorski izdelek med dvema vektorjem vedno povzroči drug vektor.
• Obseg vektorskega izdelka v zakonu o Biot-Savart je:kje θ je kot med dl in r.
• Najti je treba vektorski izdelek prej Če je integralna ločljivost razrešena, se reši integral vsake od pridobljenih komponent.
• Potrebno je potegniti situacijo in vzpostaviti ustrezen koordinatni sistem.
• Kadar koli opazimo obstoj neke simetrije, ga je treba uporabiti za shranjevanje časa izračuna.
• Ko obstajajo trikotniki, sta teorem pitagore in teorema za kosinus v veliko pomoč pri vzpostavljanju geometrijskega razmerja med spremenljivkami.

Kako se izračuna?

S praktičnim primerom izračuna B Za pravokotno žico se ta priporočila uporabljajo.

Lahko vam služi: Torna obremenitev: Lastnosti in Coulomb Law

Primer

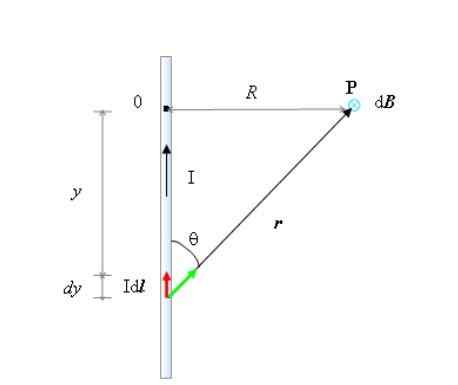
Izračunajte vektor magnetnega polja, ki ga zelo dolga pravokotna žica proizvaja v točki p prostora, glede na prikazano sliko.

Geometrija, potrebna za izračun magnetnega polja v točki P, neskončno dolge tokovne žice. Vir: Self Made.

Iz slike morate:

• Žica je usmerjena navpično, s tokom, ki teče navzgor. Ta naslov je +in v koordinatnem sistemu, katerega izvor je na mestu oz.
• θ je kot med dl in r In res je tudi, da: 
• V tem primeru v skladu s pravilom desnega palca, B V točki P je usmerjena v papir, zato je označen z majhnim krogom in "x" na sliki. Ta naslov bo vzet kot -z.
• Pravi trikotnik, katerega noge so in in R, Obe spremenljivki povezuje glede na izrek Pythagoras: r²= R²+in²

Vse to je nadomeščeno v integralu. Vektorski ali navzkrižni izdelek je označen z njegovo magnitudo plus smer in njen pomen:

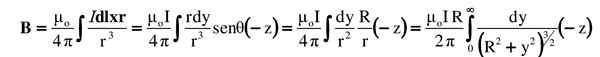
Predlagani integral se išče v integralni tabeli ali pa ga reši ustrezna trigonometrična substitucija (bralec lahko rezultat preveri s pomočjo uporabe y = rtg θ):

Rezultat se strinja s pričakovanim: obseg polja se zmanjšuje z razdaljo r in se sorazmerno poveča z intenzivnostjo toka I.

Medtem ko je neskončno dolga žica idealizacija, je pridobljeni izraz zelo dober pristop k polju dolge žice.

Z zakonom o biot in Savart je mogoče najti magnetno polje drugih porazdelitve visoke simetrije, kot je krožna spirala, ki prevaža tok ali zložene žice, ki združujejo pravokotne in krivinearne segmente.

Seveda mora biti problem visoko stopnjo simetrije. Sicer je alternativa številčno reševanje integrala.

Reference

1. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 2. Mehika. Uredniki učenja Cengage. 367-372.