Matematična enakost
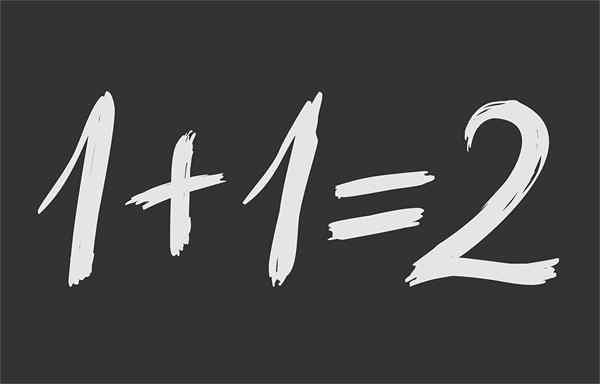
- 910
- 265
- Roman Schamberger
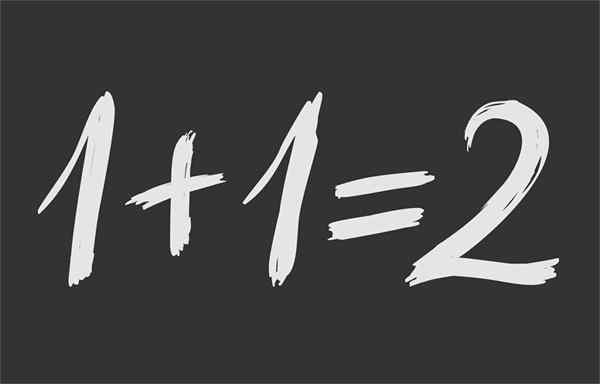 Slika 1.- Matematična enakost zagotavlja, da je 1 + 1 enak 2
Slika 1.- Matematična enakost zagotavlja, da je 1 + 1 enak 2 Kaj je matematična enakost?
Matematična enakost zagotavlja, da sta dva izraza enaka ali drugačna, popolnoma enakovredna. Ti izrazi so lahko raznolike narave, na primer številke, črke, ki simbolizirajo količine ali velikosti, kombinacije števil in črk, matric in še več.
Simbol, ki se uporablja za označevanje enakosti v matematičnem jeziku, je simbola dveh vzporednih in vodoravnih vrstic, ki je v tiskanem besedilu dobro znani simbol "=". Na primer, če imate tri jabolka, lahko napišete naslednjo enakost:
Število jabolk = 3
Stavek "število jabolk" je član leve, številka 3.
Ker je mogoče na različne načine pisati številčne količine, se za njihovo označevanje uporablja enakost. Če upoštevamo določen primer za ponazoritev točke, obstaja več načinov, kako napisati številko 4, razen najbolj očitnega, ki je 4 = 4, lahko z matematično enakostjo zapišemo naslednje:
2 + 2 = 4
6 - 2 = 4
8 ÷ 2 = 4
2 × 2 = 4
22 = 4
Enakost, prikazana tukaj, je resnična, vendar enakost morda ni, na primer 10 + 5 = 20 je napačna, saj 10 + 5 = 15.
Zagotovo bralec pozna druge načine, kako napisati številko 4. Upoštevajte, da so izrazi na vsaki strani enakosti lahko številke, besede, črke, ki simbolizirajo količine ali druge simbole, na primer:
x + 1 = 7
do2B - 1 = xy
f (x) = 2x2
Matematiki niso vedno uporabljali simbola enakosti, zato so bile stare matematične pogodbe zelo obsežne.
Pripisuje se matematiku in doktorju Robert Reming (1510-1558), rojenem v Walesu, ustvarjanju simbola enakosti "=", tako znano vsem danes. Ne pozabite, navidezno utrujeni od pisanja ves čas stavek "tako kot" v eni od svojih matematičnih pogodb, se je odločil, da bo na svojem mestu skrajšal sorodnike vzporedne črte.
Vam lahko služi: petegonalna prizma: značilnosti, deli, točki, robovi, volumenLastnosti matematične enakosti
Naslednje lastnosti omogočajo pravilno delo z matematično enakostjo. So aksiomatični, zato ne potrebujejo demonstracije:
1.- Odsevna lastnost
Ta lastnost določa, da je kateri koli znesek enak sebi. Zlasti, ker je katero koli število enako sebi, je mogoče zapisati enake:
5 = 5
36.35 = 36.35
Če je znesek dobeseden ali je kombinacija črk in številk, je tudi sam enak:
3x = 3x
do2Pr-1 = a2Pr-1
2.- Lastnost simetrije
Zneke ali člane na obeh straneh enakosti lahko zamenjate brez izgubljene veljavnosti. Torej, če je na levi strani simbola "=" zapisano na desni strani in tisto, kar je na vaši desni, je postavljeno na levo.
Na primer, izraz 5 + 2 = 7 je enakovreden temu: 7 = 5 + 2. Na enak način:
12 + 8 = 20; 20 = 12 + 8
x + 1 = 3; 3 = x + 1
x - z = y; y = x - z
3.- Prehodna lastnost
Ta lastnost se nanaša na enakovrednost enakosti. Če imata dva enakost skupnega člana, potem sta tudi enaka, saj na splošno:
Če je "x = y" in "y = z" potem x = z
Za ponazoritev te lastnosti razmislite o teh dveh številčnih enakosti: 2 + 2 = 4 in 6 - 2 = 4. Ker sta oba enaka 4 (imata skupnega člana), je mogoče zapisati naslednje, ne da bi izgubili kakršno koli veljavnost:
2 + 2 = 6 - 2
Še en primer, tokrat s črkami:
Da x + 1 = 5
In
A - b = 5
Tako:
x+1 = a - b
4.- Lastnost odpovedi
Enakost ni spremenjena, če je v obeh članih enak znesek, ki dodaja (ali odšteje) in se odloči, da to odpravi ali prekliče. To je lastnost odpovedi vsote.
Kot primer vzemite naslednjo numerično enakost, v kateri se 10 pojavlja tako v članu desne kot v tistem na levi:
Lahko vam služi: trigonometrične funkcije: Osnovne, v kartezijanski ravnini, primeri, vadba2 + 2 + 10 = 6 - 2 + 10
Številka 10 je mogoče preklicati, ne da bi enakost izgubila veljavnost, pri čemer ostane še ena krajša enakost in enakovredna prejšnji:
2 + 2 = 6 - 2
V enakosti (10 ÷ 2) - 3 = 5 - 3 celo število - 3 spada v oba člana enakosti in se zdi, da se lahko dodaja, zato je mogoče preklicati in pridobiti:
10 ÷ 2 = 5
Zgodi se tudi z dobesednimi količinami, na primer:
Da x + 2y + z = −a + b + z
Potem lahko "z" prekličete, saj ga na obeh straneh enakosti najdemo kot dodajanje (in z istim znakom).
Pri tem rezultati:
x + 2y = −a + b
Prav tako lahko določi lastnost odpovedi množenja. Če isti znesek C pomnoži oba člana enakosti, lahko ta znesek prekliče, na primer:
Cx = cy
Potem lahko C prekličete, da dobite preprosto:
x = y
5.- Lastnost enakomernosti
Enakost ostaja nespremenljiva z dodajanjem, odštevanjem, množenjem ali deljenjem z isto količino na obeh straneh istega.
Na primer, mora biti 8 + 5 = 13, če se oba člana pomnožita po določeni poljubni številki C = 2, ostaja enakost:
(8+5) × 2 = 13 × 2
13 × 2 = 26
Matematični enaki razredi
Obstajajo različne vrste matematične enakosti, zato so razvrščene po svojem najboljšem razumevanju v:
-Identitete, So enakost, v kateri sta oba člana enaka:
2 = 2
x = x
2x = x + x
in tako naprej.
-Enačbe, To so enake, pri katerih se pojavlja ena ali več neznank in velja za določene vrednosti, torej enakost ni izpolnjena za nobeno poljubno vrednost, zato so znani tudi kot tudi kot pogojne enakosti. Primeri:
x + 1 = 5
x3 = 27
A + b = 40
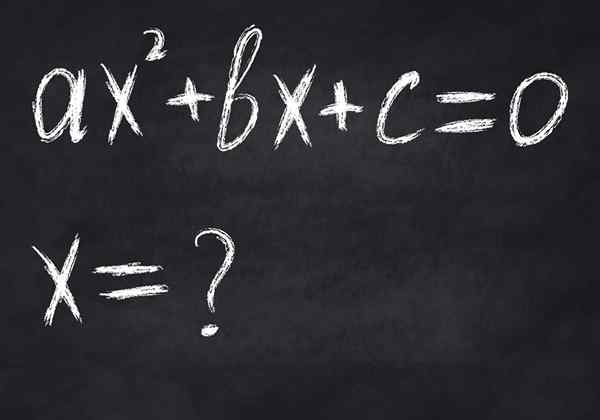 Slika 2.- Enačba je pogojna matematična enakost, saj je izpolnjena le za določene spremenljive vrednosti. Slika prikazuje enačbo druge stopnje, ki ima kvečjemu dve resnični rešitvi
Slika 2.- Enačba je pogojna matematična enakost, saj je izpolnjena le za določene spremenljive vrednosti. Slika prikazuje enačbo druge stopnje, ki ima kvečjemu dve resnični rešitvi -Enakovrednosti, V njih je član leve enakovredne tistemu na desni, tudi če ni enakovreden, na primer v: 23 = 8.
Vam lahko služi: načelo aditiva-Formule, To je enakost, ki se vedno izpolnjuje za vrednosti neodvisne spremenljivke, kot v dobro znani formuli za razdaljo D, odvisno od časa t mobilnega telefona z enotnim pravokotnim gibanjem: D = v ∙ t
Rešene vaje
Vaja 1
Napišite številko 10 do štiri različne in enakovredne enakosti.
Rešitev
Vse te enakosti izražajo številko 10, vendar na različne načine:
5 × 2 = 10
11-1 = 10
101= 10
20 ÷ 2 = 10
Vaja 2
Kakšna je vrednost x, ki izpolnjuje enakost x + 1 = 3?
Rešitev
Ta enakost je enačba, saj vrednost x ni znana. Uporaba lastnosti 5, če se doda izraz x + 1 = 3 (−1) na obeh straneh simbola "=", ostaja enakost:
x + 1 + (−1) = 3 + ( - 1)
Pri dodajanju (−1) članu leve in operacije je razrešena, "X" je sam na levi strani enakosti, se ta postopek imenuje odmik:
x + 1 - 1 = 3−1
x = 2
Zato je vrednost, ki izpolnjuje to enakost, x = 2.
Vaja 3
Če ima mobilni telefon z enotnim pravokotnim gibanjem hitrost 2.5 m/s, kakšna je razdalja, ki poteka po 3 sekundah?
Rešitev
Uporabljena je formula, ki je bila vidna v prejšnjem razdelku, D = v ∙ t, v katerem je nadomeščena vrednost V:
D = 2.5 ∙ t
Izraz postane enakost, ko je t = 3 sekunde in je operacija razrešena:
D = 2.5 ∙ 3 m = 7.5m
Kar ima za posledico enakost:
D = 7.5m
Reference
- Barnett, r. 2000. Pred skušnjavo. 4. Izdaja. McGraw Hill.
- Larson, r. 2012. Pred skušnjavo. 8. Izdaja. Cengage učenje.
- Pérez, v. Lastnosti algebrske enakosti. Okrevano od: matematika.Laguia2000.com.
- Lastnosti enakosti. Pridobljeno iz: PPS.K12.Ali.nas.
- Stewart, J. 2007. Pred izračunom: matematika za izračun. 5. Izdaja. Cengage učenje.

