Icosagono

Kaj je icogon?

A Icosagono ali Isodecagon Je poligon, ki ima 20 strani. Poligon je ravna figura, ki jo tvori končno zaporedje linijskih segmentov (več kot dva), ki obdaja območje ravnine.

Vsak segment linije se imenuje stran in križišče vsakega para strani se imenuje točka. Glede na število strani poligoni prejmejo določena imena.

Najpogostejši so trikotnik, štirikolesni, pentagon in šesterokotnik, ki imajo 3, 4, 5 in 6 strani, vendar jih je mogoče zgraditi s številom zaželenih strani.

Značilnosti icogona

Spodaj so nekatere značilnosti poligonov in njihove uporabe v icogonu.

1- Klasifikacija

Icosgono, ki je poligon, je mogoče razvrstiti kot reden in nepravilen, kjer se navadna beseda nanaša na dejstvo, da imajo vse strani enake dolžine in notranje kote merijo enako; Sicer se reče, da je ikosagon (poligon) nepravilen.

2- izodekagon

Navadni icosgon se imenuje tudi navadni izodogon, saj je za pridobitev običajnega icosgon -garge, kar je treba storiti.

3- perimeter

Za izračun oboda "P" navadnega poligona se število strani pomnoži po dolžini vsake strani.

V posebnem primeru icogona je obod enak 20xl, kjer je "L" dolžina vsake strani.

Na primer, če imate redni 3 cm stranski ikosagon, je njegov obod enak 20x3cm = 60 cm.

Jasno je, da če je izokagon nepravilen, prejšnje formule ni mogoče uporabiti.

V tem primeru je treba 20 strani dodati ločeno, da dobimo obod, to je, da je obod "P" enak ∑li, z i = 1,2,…, 20.

4- diagonala

Število diagonalov "D", ki imajo poligon, je enako N (N-3)/2, kjer N predstavlja število strani.

V primeru icogona mora biti d = 20x (17)/2 = 170 diagonalov.

5- vsota notranjih kotov

Obstaja formula, ki pomaga izračunati vsoto notranjih kotov navadnega poligona, ki jo je mogoče uporabiti za navadni icosgon.

Formula je sestavljena iz odštevanja 2 na število strani poligona in nato pomnoži to številko za 180 °.

Način, kako se ta formula pridobi, je, da lahko poligon N strani razdelimo na trikotnike N-2 in z dejstvom, da je vsota notranjega kota trikotnika 180 °, dobimo formulo.

Na naslednji sliki je ponazorjena formula za običajni Enegon (9 -stranski poligon).

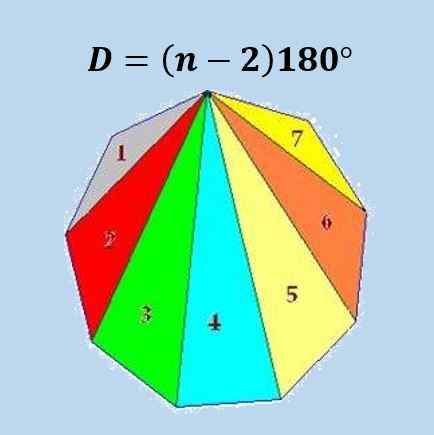
Z uporabo sprednje formule je pridobljeno, da je vsota notranjih kotov katerega koli ikosagona 18 × 180 ° = 3240 ° ali 18π.

6- območje

Za izračun območja rednega poligona je zelo koristno poznati koncept apotema. Apotheme je pravokotna črta, ki sega od središča rednega poligona do sredine katere koli strani.

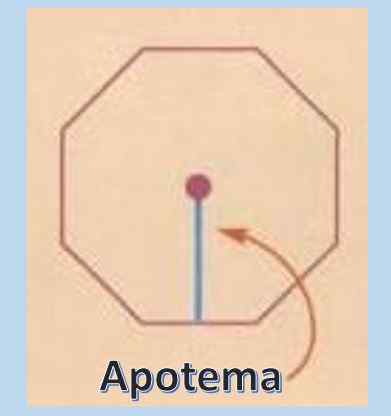
Ko je dolžina apotema znana, je območje navadnega poligona A = PXA/2, kjer "P" predstavlja obod in "A" apotheme.

V primeru običajnega ikosagona, ki ga imate na svojem območju, je A = 20xlxa/2 = 10xlxa, kjer je "L" dolžina vsake strani in "A" njena apotema.

Po drugi strani pa, če imate nepravilen poligon N strani, za izračun njenega območja je poligon razdeljen na N-2 znane trikotnike, potem se izračuna območje vsakega od teh N-2 trikotnikov in na koncu vse to so dodana območja.

Zgoraj opisana metoda je znana kot triagulacija poligona.

Reference

1. Geometrijski elementi: s številnimi vajami in geometrijo kompasa. Univerza v Medellinu.
2. Iger. (s.F.). Matematika Prvi semester Tacaná. Iger.