HEPTADECágono Lastnosti, diagonale, obod, območje

On Heptadecágono To je redni poligon 17 strani in 17 vrhov. Njegova konstrukcija je mogoče izvesti v evklidskem slogu, to je uporaba samo pravila in kompasa. To je bil velik genij matematike Carl Friedrich Gauss (1777-1855), ki je štel le 18 let, ki je našel postopek za njegovo gradnjo leta 1796. 

Očitno se je Gauss vedno počutil zelo naklonjen tej geometrijski figuri, do te mere, da je od dneva, ko je odkril svojo gradnjo, odločil, da bo matematik. Govori se tudi.

Slika 1. Heptadecágono je redni poligon 17 strani in 17 vrhov. Vir: f. Zapata.

Gauss je našel tudi formulo, da bi ugotovil, kateri redni poligoni imajo možnost zgraditi s pravilom in kompasom, saj nekateri nimajo natančne evklidske konstrukcije.

[TOC]

Značilnosti Heptadecágona

Kar zadeva njegove značilnosti, kot vsak poligon, je vsota njegovih notranjih kotov pomembna. V običajnem poligonu n strani, vsota daje:

Sa (n) = (n -2) *180 °.

Za heptadecágono število strani n je 17, Kar pomeni, da je vsota njegovih notranjih kotov:

SA (17) = (17 - 2) * 180º = 15 * 180º = 2700 °.

Ta vsota, izražena v radianesu, je taka:

SA (17) = (17 - 2) * π = 15 * π = 15π

Iz prejšnjih formul je mogoče enostavno razbrati, da ima vsak notranji kot heptadekagona natančen α ukrep, ki ga daje:

α = 2700 °/17 = (15/17) π radianes

Iz tega sledi, da je notranji kot približno:

α ≈ 158,824 °

Diagonale in obod

Diagonalni in obod so drugi pomembni vidiki. V katerem koli poligonu je število diagonalov: 

D = n (n - 3) / 2 in v primeru Heptadecágono, kot je N = 17, Moraš D = 119 diagonale.

Vam lahko služi: trinomial

Po drugi strani pa, če je znana dolžina vsake strani heptadecágono, potem obod običajnega heptadecágona preprosto dodaja 17 -krat večjo dolžino ali tisto, kar je enakovredno 17 -krat večja od dolžine d Na vsaki strani:

P = 17 D

Obod Heptadecágona 

Včasih je znan samo radio r heptadecágono, zato je treba razviti formulo za ta primer.

V ta namen je koncept apotem. Apotheme je segment, ki sega od središča rednega poligona do sredine točke na eni strani. Apotem glede na stran je pravokotno na to stran (glej sliko 2).

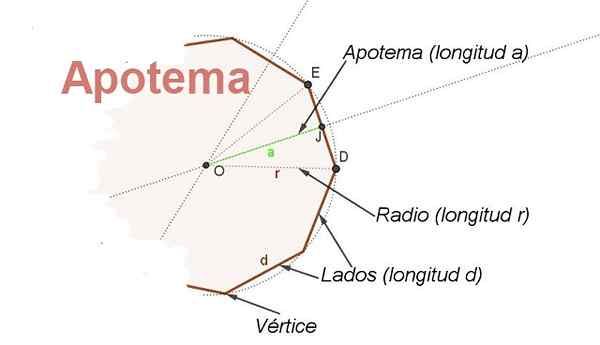Slika 2. Prikazani so deli običajnega radijskega poligona in njegovega apotema. (Lastna izdelava)

Poleg tega je apotem bisektor kota z osrednjo točko in stranice na dveh zaporednih točkah poligona, to omogoča iskanje razmerja med radiom r in stran d.

Če se pokliče β do osrednjega kota Srček In ob upoštevanju tega apotema Oj je bisektor, ki ga imate Ex = d/2 = r sen (β/2), kjer imate odnos, da najdete dolžino d na strani poligona, ki je poznal svoj radio r in njegov osrednji kot β:

D = 2 r sin (β/2)

V primeru Heptadecágona β = 360 °/17 Za tisto, kar imate:

D = 2 R Sen (180 °/17) ≈ 0,3675 r

Končno je formula oboda Heptadecágona, ki je znana, da je njegov polmer:

P = 34 R Sen (180 °/17) ≈ 6.2475 r

Obod heptadekagona Pcir = 2π r ≈ 6.2832 r.

Območje

Za določitev območja Heptadecágono se bomo sklicevali na sliko 2, ki prikazuje stranice in apotem rednega poligona n strani. Na tej sliki trikotnik Eod Ima površino, ki je enako bazi d (stran poligona) po višini do (Poligon apothem) deljeno s 2:

Lahko vam služi: niz moči: primeri in vaje

Eod = (d x a) / 2

Torej ta znana apotema do heptadecágona in strani d istega je:

HEPTADECágono območje = (17/2) (d x a)

Območje glede na stran

Če želite dobiti formulo za območje Heptadecágono, ki pozna dolžino svojih sedemnajstih strani, je treba doseči razmerje med dolžino apotema do in stran d.

V zvezi s sliko 2 imate naslednje trigonometrično razmerje:

Tan (β/ 2) = npr/ oj = (d/ 2)/ a, biti β do osrednjega kota Srček. Torej ta apotem do lahko izračunamo, če je dolžina znana d z strani poligona in osrednjega kota β:

A = (d/2) kotan (β/2)

Če se ta izraz za apotem zdaj zamenja, v formuli območja Heptadecágono, pridobljenega v prejšnjem razdelku, imate:

Območje Heptadecágono = (17/4) (D²) Kotan (β/2)

Biti β = 360 °/17 Za Heptadecágono, tako da končno imate želeno formulo:

Območje Heptadecágono = (17/4) (D²) Kotan (180 °/17)

Območje glede na radio

V prejšnjih razdelkih je bilo najdeno razmerje med D strani rednega poligona in njegovim r radio r, naslednje: naslednje: naslednje:

D = 2 r sin (β/2)

Ta izraz za d Vstavljen v izraz, pridobljen v prejšnjem razdelku za območje. Če so izvedene ustrezne substitucije in poenostavitve, dobimo formulo, ki omogoča izračun območja Heptadecágono:

Območje Heptadecágono = (17/2) (r²) Sin (β) = (17/2) (r²) Sen (360 °/17)

Približni izraz za to območje je:

Območje Heptadecágono = 3.0706 (r²) 

Kot je bilo pričakovano, je to območje nekoliko manj kot območje kroga, ki omejuje Heptadecágon Do_Cirm = π r² ≈ 3.1416 r². Če sem natančen, je za 2% nižji od tistega, ki je bil omejen krog.

Vam lahko služi: območje rednega in nepravilnega pentagona: kako se jemlje, vaje

Primeri

Primer 1

Da ima heptadecágono 2 cm strani, kakšna vrednost naj ima polmer in premer obloženega oboda? Poiščite tudi vrednost oboda.

Če želite odgovoriti na vprašanje, se je treba spomniti odnosa med stranjo in polmerom običajnega poligona N strani:

 D = 2 r sena (180 ° / n)

Za Heptadecágono N = 17, torej D = 0,3675 r, Z drugimi besedami

Premera 10.8844 cm.

Obod 2 cm stranskega heptadecágona je p = 17* 2 cm = 34 cm.

Primer 2

Koliko je območje navadne strani Heptadecágono de 2 cm?

Treba se je sklicevati na formulo, prikazano v prejšnjem razdelku, ki omogoča iskanje območja heptadecágona, ko je dolžina d Na njegovi strani:

Območje Heptadecágono = (17/4) (D²) / Porjavelo (180 ° / 17) 

Pri zamenjavi D = 2 cm v sprednji formuli dobimo:

Območje = 90,94 cm

Reference

1. C. In. Do. (2003). Elementi geometrije: z vajami in geometrijo kompasa. Univerza v Medellinu.
2. Campos, f., Cerecedo, f. J. (2014). Matematika 2. Uredniška skupina Patria.
3. Osvobojen, k. (2007). Odkrijte poligone. Benchmark Education Company.
4. Hendrik, v. (2013). Splošni poligoni. Birkhäuser.
5. Iger. (s.F.). Matematika Prvi semester Tacaná. Iger.
6. Jr. Geometrija. (2014). Poligoni. Lulu Press, Inc.
7. Miller, Heeren in Hornsby. (2006). Matematika: sklepanje in aplikacije (deseta izdaja). Pearson Education.
8. Patiño, m. (2006). Matematika 5. Uredništvo Progreso.
9. Sada, m. Rednih 17 strani s pravilom in kompasom. Okreval od: geogebra.org
10. Wikipedija. Heptadecágono. Okrevano od: je.Wikipedija.com