Matematika

Euclidska geometrija

Euclidska geometrija

Pojasnjujemo, kaj je evklidska geometrija, njena zgodovina, elementi in navajamo več primerov

Euclid iz Aleksandrije in njegovih elementov, Jusepe de Ribera, sosednja vrata, dve neparalni črti in črta, ki jih razreže, kar ponazarja peti postulat. Vir: Wikimedia Commons.

Kaj je evklidska geometrija?

The Euclidska geometrija To je tisto, ki ga urejajo tisti postulati Euclid de Alejandría, grški geometer, ki je živel proti 300 do.C, v čast je ta disciplina imenovana, saj jo je prva sistematizirala.

Ta veja matematike preučuje lastnosti linij, ravnin, kotov in geometrijskih oseb, kot so poligoni, obod in drugi koniki. Od tod tudi njegov pomen v znanosti in inženiringu, katerega razvoj je močno spodbudil.

Po drugi strani je bila evklidska geometrija prva natančna znanost, saj se je začela pot sistematizacije znanosti, pa tudi uporaba logike za prikaz iz nekaj aksiomov, številnih predlogov, imenovanih teoreme, da bi opisali lastnosti geometrijskih predmetov.

Zgodovina

Geometrija ima dolgo zgodovino, saj je zanimanje za človeštvo zelo staro in osrednja os evklidske geometrije je delo Predmete, modrega evklida iz Aleksandrije, mesta, ki se nahaja v Egiptu, in ki je živel v četrtem stoletju.C.

Takrat so bile znane najpomembnejše lastnosti številnih figur in geometrijskih teles. Obstajalo je obsežno znanje o geometriji, vendar je bilo vse empirično in manjkalo sistematizacije.

Nato je kralj Egipta Ptolomeja in zaupal že tako znanemu učitelju Euclida, katerega šola je bila v Aleksandriji, da bi organiziral vse doslej matematično in geometrijsko znanje, vključno z teoremi in nepremičninami.

Euclides je začel delati in poleg svojih učencev je napisal svoje delovne elemente, ki jih je razdelil na trinajst knjig kot poglavja. To delo bi postalo referenca za geometrijo za prihodnje generacije.

Vam lahko služi: zaporedni derivati

Elementi Euclida

Vsebina elementov je organizirana na naslednji način:

  • V knjigah se razvija ravna geometrija.
  • V knjigah V in sem videl teorijo o sorazmerju.
  • IX knjige so namenjene aritmetiki.
  • Nepreizbeljivost se pojavlja v knjigi x,
  • Geometrija prostora v knjigah xi do xiii.

Euclidska geometrija je bila osnova za številne posteriorne geometrijske dogodke in se trenutno poučuje v vseh šolah na svetu.

Prav tako ima vrtino, da je prvo delo, ki vključuje skrbne demonstracije, ki temeljijo na logičnem sklepanju, in tudi v skladu s tem, da je ta čas v skladu s telesom geometrijskega in matematičnega znanja.

Osnovni elementi evklidske geometrije

Euclidska geometrija je zgrajena okoli štirih osnovnih elementov, opisanih v knjigi I elementov:

  1. Mesto
  2. Naravnost
  3. Stanovanje
  4. Prostor

1. Mesto

A mesto Nima dimenzij ali delov in se od druge točke loči po svoji lokaciji. Če sta dve točki A in B različni, je to zato, ker imata različne položaje, ki so označene skozi dobro znane kartezijske koordinate (x, y), če je točka v ravnini ali koordinate (x, y, z) Če je v vesolju.

Omeniti velja, da kartezijanski sistem ni del Predmete Euclida, vendar se je pojavil veliko kasneje v 1600 letih in je posledica Renéja Descartesa.

2. Naravnost

The naravnost Gre za neskončno zbirko točk in ima samo dolžino, ne širino. Del tega je običajno narisan, pri čemer se puščice v obeh poudarja, da se črta nadaljuje v nedogled.

3. Stanovanje

A stanovanje To je neomejena površina, tako da ima dve dimenziji in od katerih je del predstavljen s kvadratom ali pravokotnikom.

Tam je v ravnini med drugim veliko geometrijskih oseb, kot so črte, odprte in zaprte krivulje in poligoni.

Vam lahko služi: splošna enačba črte, katere naklon je enak 2/3

4. Prostor

Končno je tu prostor S svojimi tremi dimenzijami, ki so sposobni nastaniti vse točke. Vsebuje letala in geometrijska telesa, za katere je značilna njihova volumen, kot so poliedri, kroglice in še več.

Te lahko veljajo za osnovne definicije evklidske geometrije, vendar poleg teh Euclides v svojem delu ponuja približno 150 raznolikih definicij.

Skupne pojme

Sestavljajo jih očitna in intuitivna dejstva, ki ne spadajo pravilno v obseg geometrije in se uporabljajo, ko se razvijajo koncepti. "Stvari" se nanašajo v zelo širokem kontekstu:

  1. Stvari enake nečemu drugemu, enake so med seboj.
  2. Če se stvari dodajo v drug sklop stvari in so vsi enaki, kakšni rezultati so tudi enaki.
  3. Če so ukradene enake stvari, so tudi preostale enake.
  4. Ko se stvari med seboj sovpadajo, je to zato, ker so enake.
  5. Celota je vedno večja od strank, vzeta ločeno.

Postulati evklidske geometrije

Postulati ali aksiomi so preproste izjave, ki veljajo za resnične in očitne, zato ne potrebujejo demonstracije.

Predstavljajo osnovo euklidijske in evklidne geometrije, ki v njihovi knjigi I vzpostavlja pet:

  1. Biti dve različni točki in B, skozi njih je samo ena vrstica, torej dve točki določata črto.
  2. Vsak pravokotni segment je mogoče razširiti za nedoločen čas, da predstavlja črto, zato vsak segment pripada črti.
  3. Če imate dve različni točki ali in a, lahko vedno narišete krog s sredino v O in polmeru, ki je enak segmentu OA.
  4. Vsi ravni koti so skladni med seboj.
  5. Glede na črto in točko P, ki ji ne pripada, je vedno mogoče.

Zadnji postulat, zlasti v prvotni različici, ni videti tako preprost kot drugi. Navaja, da:

Vam lahko služi: Heptagon

"Če ravna črta, ki pade na dve drugi vrstici, naredi dva notranja kota na isti strani manj kot dva ravna kota, so povedali ravne črte, ki so razširjene v nedogled, so (sekajo) na strani dva ravna kota ".

To pomeni, da prvotno postulat 5 vzpostavi pogoj, tako da dve vrstici nista vzporedni. Vendar je jasnejše, ko je napisano tako, da ponazarja nasprotno, to je vzporednost vrstic.

Primeri evklidske geometrije

Primer 1

Obstajajo tri različne točke, označene s črkami A, B in C.

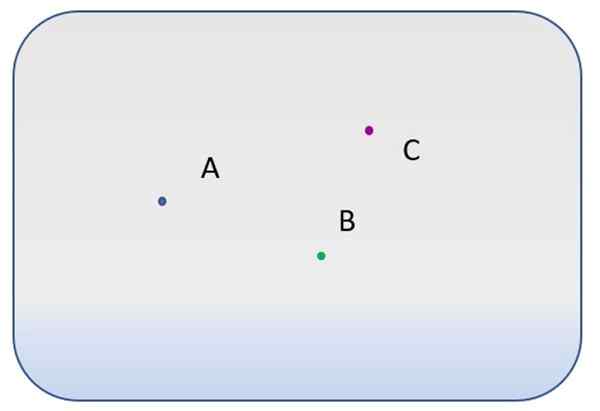
  1. Koliko različnih vrstic gre skozi točko A?
  2. In koliko jih je mogoče narisati med točkami A in B? In med A in C?
  3. Ali je mogoče narisati črto, do katere točke A, B in C?

Odgovor na

Po mnenju Postulate I lahko skozi A narišete neskončne ravne črte, saj sta za določitev črte potrebna dve točki.

Odgovor b

Entre A in B je mogoče narisati le črto. In tudi med A in C.

Odgovor c

Ni mogoče, da črta hkrati vsebuje a, b in c.

Primer 2

Zahteva se, da korak za korakom zgradi enakostranični trikotnik (vse njene strani so enake), saj pozna eno od njegovih strani, ki je segment AB in v vsakem koraku označuje postulat ali skupni pojem, ki se uporablja v konstrukciji v.

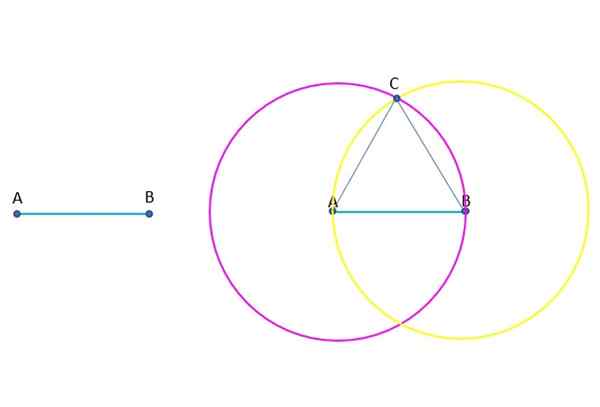Konstrukcija enakostraničnega trikotnika ABC. Vir: f. Zapata.

Odgovor

Korak 1

Krog s središčem v A in Radio AB je narisan. To je vedno mogoče, po Postulat III.

2. korak

Narisan je še en obod s centrom v B in Radio AB in Postulat III se ponovno uporabi.

Korak 3

Oba okolica, ki imata enak polmer, sta razrezana na točki c. Zdaj lahko narišete segmente, ki se združujejo z A in B, v skladu s Postulat I.

Ti segmenti so radijski sprejemniki oboda, zato so ukrepi AC in BC enaki kot pri AB, v skladu s skupnim pojem 1. Potem je trikotnik ABC enakostraničen.