Analitična geometrija

Pojasnjujemo, kaj analitična geometrija, njena zgodovina, kaj so študije in aplikacije

Kaj je analitična geometrija?

The analitična geometrija To je veja matematike, v kateri sta geometrija in algebra združena, da bi rešili različne geometrijske težave z algebrskimi tehnikami.

Uporabite koordinatne sisteme, kot je kartezijanski koordinatni sistem, ki dolguje njeno ime René Descartes. Na ta način je mogoče povezati krivulje v ravnini in v vesolju z algebrskimi enačbami.

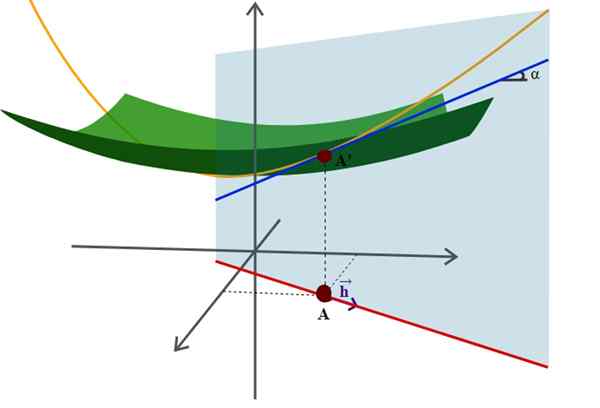
Diagram površine v vesolju in njegovega usmerjenega izpeljanja, ki je ena izmed številnih naprednejših aplikacij analitične geometrije. Vir: Wikimedia Commons.

Primer tega je dobro znana enačba polmera r -riortion, osredotočena na izvor koordinatnega sistema:

Nedvomno je v mnogih primerih preprosto delati z algebrskim izrazom krivulje, kot pa s samim geometrijskim prikazom. To je pri izračunu križišč med krivuljami ali iskanju tangentnih ali sušilnih linij do njih.

Podobno je s pomočjo analitične geometrije mogoče grafiko postaviti funkcije. In kot je znano, funkcije omogočajo modeliranje znanosti in inženirskih težav. Zato je v učnih načrtih kariere, povezanih s temi področji znanja, prisotna analitična geometrija.

Kratka zgodovina analitične geometrije

Analitična geometrija ima svoj izvor v prvi polovici 17. stoletja po roki dveh pomembnih francoskih matematikov: Renéja Descartesa (1596-1650) in Pierre de Fermat (1601-1665).

Rene Descartes

Vendar lahko rečemo, da se njegovo ozadje vrača v stoletja, grškemu matematike Apollonius iz Pergama (262-190 a.C.). Napisal je traktat o konikih, ki jim je podelil njihova imena: obod, elipse, prispodoba in hiperbola.

Lahko vam služi: sestavljena sorazmernost: razlaga, tri sestavljene pravila, vaje

Tako je bilo delo Apollonio osnova za veliko kasneje, da sta francoski René Descartes in Pierre de Fermat postavila temelje analitične geometrije, neodvisno. Toda Descartes velja za oče te znanosti, saj je prvi objavil svoja dela.

Descartes, Fermat in Euler

V govoru metode 1637 je Descartes poenotil dve disciplini, ki sta bili do takrat ločeni: algebra in geometrija. Descartes v svojem delu uvaja kartezijanski koordinatni sistem, da poišče točke v letalu in v vesolju.

Prav tako uporablja algebrske enačbe drugega debele z dvema spremenljivkama, da opiše stožčaste odseke in je namenjen reševanju geometrijskih težav z njimi. Tudi ustvariti dober del matematične zapise, ki se trenutno uporablja.

Pierre de Fermat je bolj povezan z optiko kot z analitično geometrijo, vendar so njihovi prispevki opazni.

Leta 1629 je Fermat nadaljeval s konicami Apolonija iz Pergamoja in ustvaril tehnike, ki sestavljajo analitično geometrijo, izumijo svoj lastni koordinatni sistem in jasno opredelijo ključni koncept o Geometrijsko mesto, s katerim se začne študija analitične geometrije.

Vendar pa Fermatova dela niso ugledala luči šele leta 1679, ki jo je objavil njegov sin, ko je matematik že umrl. Zaradi tega je očetovstvo analitične geometrije pripisano Descartesu.

Nato je francoski matematiki švicarski Leonardo Euler (1707-1783) vzpostavil formalne baze analitične geometrije. Euler je v ravnino in prostoru predstavil več koordinatnih sistemov: pravokotne, polarne in poševne koordinate, pa tudi transformacije iz enega sistema v drugega.

Vam lahko služi: Kako so informacije, pridobljene v anketi?

Euler je v svojih delih o analitični geometriji poglobil klasifikacijo različnih krivulj v skladu s stopnjo reprezentativne algebrske enačbe (tretji in četrti red) in intenzivno preučeval njegove lastnosti, enačbe tangentov, krivulje, simetrije in veliko več.

Kaj študira analitična geometrija?

Na splošno se analitična geometrija osredotoča na preučevanje geometrijskih elementov, kot so točke, segmenti, črte, krivulje, površine in količine. Če to storite, kot je navedeno zgoraj, vzpostavlja algebrske enačbe, ki opisujejo in povezujejo te elemente, kar omogoča njihovo upravljanje z algebrskimi tehnikami.

Glavni cilji analitične geometrije so na zelo povzetek naslednji:

1. Vzpostavite kartezijanski koordinatni sistem in polarni koordinatni sistem, da poiščete točke v ravnini, pa tudi njegovo razširitev na točke v vesolju.
2. Narišite segmente, ravne, krivulje in površine na kartezijanski ravnini in prostoru.
3. Ugotovite enačbe, ki analitično opisujejo krivuljo in konstrukcijo le -te na ravnini in/ali prostoru, pa tudi preučevanje vseh njegovih lastnosti.
4. Razvrstite krivulje, površine in količine.
5. Izperete temeljne formule za reševanje težav na pomembnih točkah, ravnih, načrtih, kotih, paralelizmu, pravokotnosti, razdaljah, križiščih, območjih in še več.
6. Rešite geometrijske težave z uporabo algebrskih metod, za katere se formule, ki se nanašajo na opazne točke, enačbe za črto, načrte, kote, razdaljo med točkami, med črtami in točkami, točkami, suhimi črtami, območja, območja in še veliko več.
7. Delajte z vektorskimi prostori in izdelki med vektorji.

Razdalja med dvema točkama

Kot primer številnih aplikacij analitične geometrije je ena najpreprostejših izračun razdalje med dvema točkama ravnine. Sta dve točki p₁ In p₂, koordinat (x₁,in₁) in (x₂,in₂) Oziroma se razdalja D med njimi izračuna z:

Vam lahko služi: trinomial

Polarne koordinate

Ravno točko je mogoče določiti skozi njegovo razdaljo "R" do izvora koordinatnega sistema, imenovanega polo, in kot, ki tvori črto, ki vsebuje točko in pol, z vodoravno osi ali polarno osi.

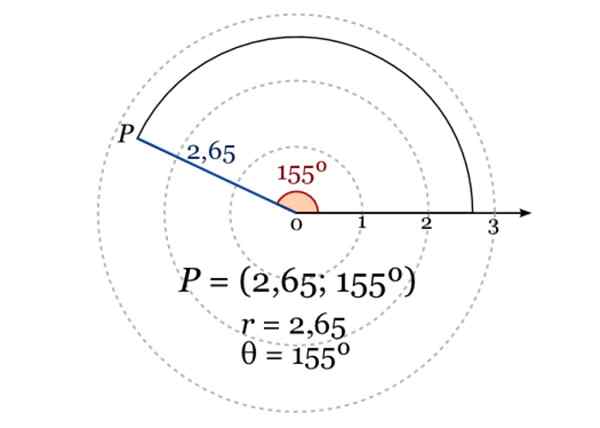Slika prikazuje polarne koordinate točke P, kjer je r = 2.65 in kot v stopinjah glede na polarno osi je 155 °. Vir: Wikimedia Commons.

Analitične aplikacije za geometrijo

Temelj neskončnega izračuna

Analitična geometrija je bistvenega pomena za razvoj neskončnoimalnega izračuna, saj olajša grafično predstavitev krivulj in funkcij ter z njimi na analitični način ustvarja modele, ki predstavljajo pojave narave.

Zemljevidi

Kartezijanski koordinatni sistem pomaga pri izdelavi zemljevidov in prepoznavanju krajev skozi širino in dolžino, kar ustreza kartezijanskim koordinatam točke v ravnini.

Topografski izračuni

V topografiji se uporabljajo različne vrste koordinatnih sistemov in so osnova njihovega študija in aplikacij. Med njimi je zgoraj opisan polarni koordinatni sistem.

Nebesna telesa

Konični odseki, opisani z analitično geometrijo, sodelujejo v pomembnih naravnih pojavih, kot so usmeritve nebesnih teles. Na primer, planeti in nekateri kometi opisujejo eliptične usmeritve okoli sonca, pri čemer se nahajajo v enem od osvetlitve.

Civilna arhitektura in konstrukcije

Številne krivulje so del arhitekturnih konstrukcij, na primer, kabli visečega mostu so lahko v obliki prispodobe.

Globalni sistemi za pozicioniranje

Globalni sistem za pozicioniranje ali GPS omogoča natančnost lokacij, pa tudi premikajoče se predmete, kot so vozila in čolni. Prav tako pomaga ljudem lažje priti do svojih destinacij in jih usmeriti na najboljše poti.