Osnovne trigonometrične funkcije v kartezijanski ravnini, primeri, vadba

The Trigonometrične funkcije Resnične spremenljivke ustrezajo kakršnemu koli kot (izražene v radiani), trigonometrični razlog, ki je lahko sinus, kosinus, tangent, cotangent, Secant in Harvester.

Na ta način imamo šest trigonometričnih funkcij: sinus, kosinus, tangent, kombajna, sušenje in cotangent.

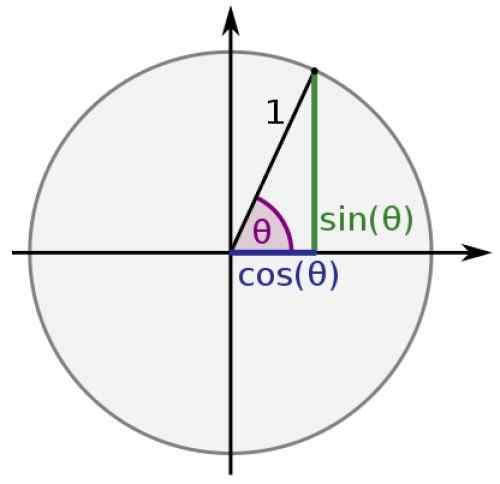
Slika 1. Trigonometrična animacija kroga. Vir: Wikimedia Commons.

Trigonometrične funkcije za kote med 0 in 2π so definirane s pomočjo enotnega oboda, radia 1 in katerih središče sovpada z izvorom kartezijanskega koordinatnega sistema: točka (0,0).

Na tem obodu lahko najdemo katero koli točko P koordinat (x, y).

Segment, ki združuje izvor s P, skupaj z ustreznimi segmenti, ki združujejo projekcije P na koordinatnih osi, sestavljajo pravokotnik trikotnik, katerega trigonometrični razlogi so znani kot količniki med stranicami trikotnika. Tako:

• sin θ = nasproti /hipotenusa cateto
• cos θ = sosednji /hipotenusa cateto
• tg θ = nasprotni cateto /sosednji cateto

In zdaj so razlogi, ki so obratni od zgoraj navedenega:

• sec θ = hipotenuza /sosednji cateto
• Škoda θ = hipotenusa /cateto nasproti
• ctg θ = sosednji cateto /nasproti cateto

V enotnem krogu je hipotenuza katerega koli trikotnika enaka 1, kategorije pa so vredne x in y, nato pa:

sin θ = y

cos θ = x

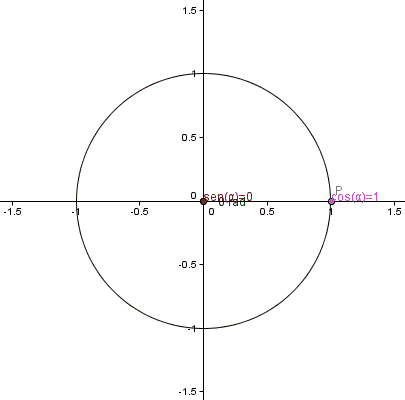
Slika 2. Desni trikotnik v krogu enote. Vir: Wikimedia Commons.

Na ta način sinusne in kosinusne funkcije vedno pridobijo vrednosti med -1 in 1, preostale pa:

tg θ = y/x

Škoda θ = 1/y

Sec θ = 1/x

Niso definirani, kdaj x tudi in Vredni so 0.

[TOC]

Trigonometrične funkcije v kartezijanski ravnini

Kot bomo videli spodaj, je za trigonometrične funkcije značilno, da so periodične. Zato niso bijektivni, razen v omejenem domeni.

Funkcija f (x) = sin x

Začenši v trigonometričnem krogu v točki P (1.0), je kot 0 radianov. Potem se polmer vrti v protirodnem smislu in funkcija Sen X raste postopoma, dokler ne doseže π/2 radianov (90 °), kar ustreza 1.Približno 571 radianov.

Vam lahko služi: dodatni koti: kaj so, izračun, primeri, vaje

Tam doseže vrednost y = 1, nato pa se zmanjša, dokler v π radianih ne doseže nič (180 °). Nato se še bolj zmanjša, saj vrednost postane negativna, dokler ne doseže –1, ko je kot 3π/2 radians (270 °).

Končno se spet poveča, dokler se v 360 ° ne vrne na nič. To je y = sin x a periodična funkcija obdobja 2π, tako da sinusna funkcija ni bivna.

Poleg tega je graf simetričen glede na točko (0,0), zato je funkcija neparna.

Potem graf y = sen x:

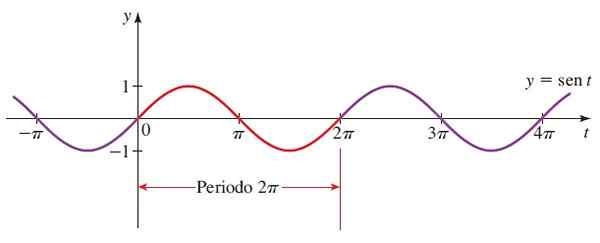Slika 3. Graf funkcije f (x) = sin x. Vir: Stewart, J. Predhodno: matematika za univerzo.

Rdeči odsek je prvo obdobje. Upoštevani so tudi negativni koti, saj se lahko polmer trigonometričnega kroga vrti v urniku.

Domena sen x = Vsa realna.

Sen x Range ali Route = [-1,1]

Funkcija f (x) = cos x

V točki P (1.0) je funkcija Coseno vredna 1 in od tam se zmanjša, doseže 0, ko je kot π/2. Nadaljujte z zmanjševanjem in negativne vrednosti, dokler ne dosežete -1 pod kotom π.

Potem se začne postopoma povečevati, dokler ne doseže 0 v 3π/2 in ponovno prevzame vrednost, ko se polmer obrnite na popoln zavoj. Od tam se cikel ponavlja, saj je Cos X periodičen in je tudi navor (simetričen okoli navpične osi).

Oblika kosinusne funkcije je enaka oblika funkcije sinusa, razen če je premaknjena π/2 glede na drugo.

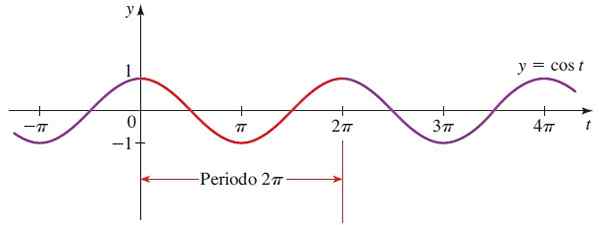Slika 4. Graf funkcije f (x) = sin x. Vir: Stewart, J. Predhodno: matematika za univerzo.

Cos x domena = Vsa realna.

Vam lahko služi: natančna ocena

Range ali cos x pot = [-1,1]

Diskontinuirane trigonometrične funkcije

Funkcije TG X, CTG X, Sec X in Hars. Ker so ti vredni 0 pod nekaterimi koti, ko se pojavijo v imenovalcu.

In ker sta sinus in kosinus periodični funkciji, so funkcije TG x, CTG x, Sec x, škoda x tudi škoda x.

Tangentna funkcija f (x) = tg x

Za tangentno funkcijo so vrednosti prekinitve: ± π/2, ± 3π/2, ± 5π/2 ... Tam je funkcija zelo velike ali zelo majhne vrednosti. Na splošno se to zgodi za vse večkratne π oblike (2N+1) π/2, tako pozitiven kot negativen, z n = 0, 1, 2 ..

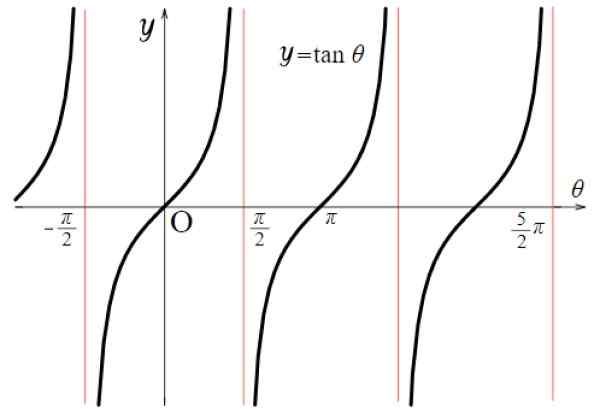Slika 5. Funkcijski graf F (x) = tg x. Vir: Wikimedia Commons.

Zato:

TG X Domena: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Rank ali TG X Tour: VSE REALES.

Upoštevajte, da se funkcija f (x) = tg x ponovi med - π/2 in + π/2, zato je njegovo obdobje π. Poleg tega je simetričen glede na izvor.

Cotangent Funkcija f (x) = ctg x

Za to funkcijo se vrednosti prekinitve pojavljajo v 0, ± π, ± 2π…, torej celotni večkratniki π.

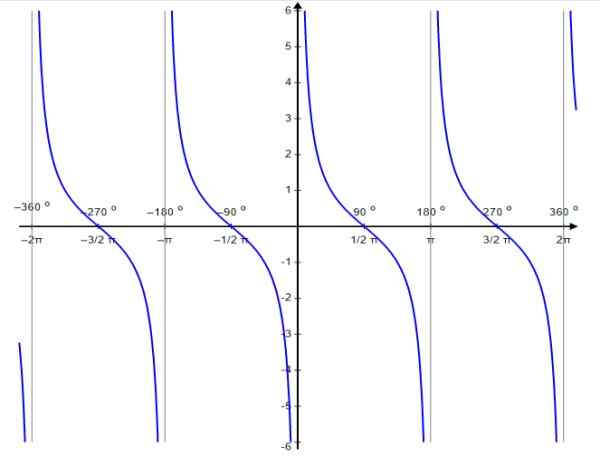Slika 6. Graf funkcije F (x) = cotg x. Vir: Wikimedia Commons.

Tako kot tangentna funkcija je tudi kotangentna funkcija periodična obdobja π. Zanjo je izpolnjeno:

CTG X Domena: D = x ∈ R / x ≠ n π; n ∈ Z

CTG X območje ali pot: VSE REALES.

Funkcija sušenja f (x) = sec x

Funkcija SEC X ima točke prekinitve v ± π/2, ± 3π/2, ± 5π/2…, kjer je cos x = 0. To je tudi periodično obdobje π in ga opazimo tudi, da funkcija v intervalu nikoli ne prevzame vrednosti (-1,1)

Vam lahko služi: cele številke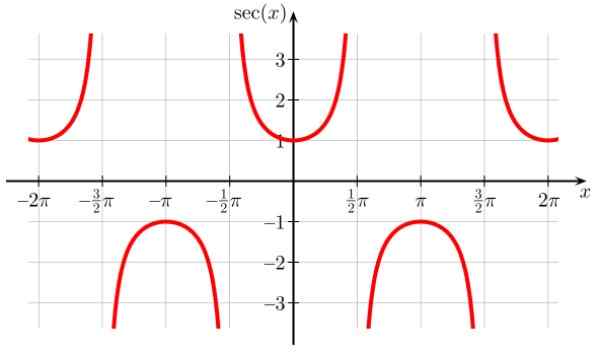 Slika 7. Graf funkcije F (x) = sec x. Vir: Wikimedia Commons.

Doma od sec x: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Sec x Range ali pot: Vsi reaji, razen (-1,1)

Funkcija žetve f (x) = škoda x

Podobno je s funkcijo sušenja, čeprav je razseljen na desno, zato so točke prekinitve 0, ± π, ± 2π in vse celotne večkratnike π. Je tudi periodična.

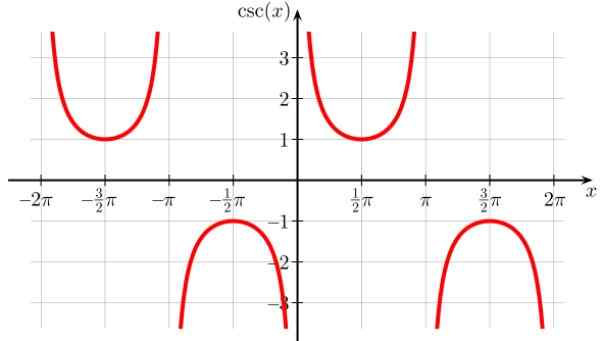Slika 8. Funkcijski graf F (x) = škoda x. Vir: Wikimedia Commons. Geek3/cc by-sa (https: // creativeCommons.Org/licence/by-sa/4.0

Škoda domena x: D = x ∈ R / x ≠ n π; n ∈ Z

Range ali harmonična pot: Vsi reaji, razen (-1,1)

Vaja rešena

6 -metrski visok moški projicira senco, katerega dolžino daje:

S (t) = 6 │cot (π.T/12) │

S S pri stopalih in t številu ur po 6. uri. Koliko je senca ob 8. uri, ob 12 m, ob 14. uri in ob 17:45?

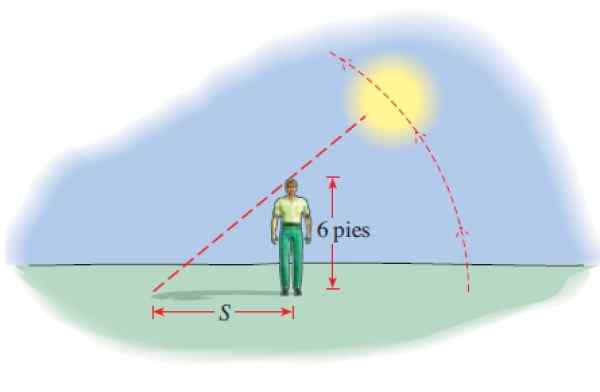
Rešitev

Oceniti moramo funkcijo za vsako od danih vrednosti, upoštevati, da mora absolutna vrednost vzeti, saj je dolžina sence pozitivna:

-Ob 8. uri sta minili 2 uri od 6. ure, torej t = 2 in s (t) je:

S (2) = 6 │cot (π.2/12) │pies = 6 │cot (π/6) │pies = 10.39 čevljev.

-Ko je 12 n, je t = 6 ur pretekel:

S (6) = 6 │cot (π.6/12) │pies = 6 │cot (π/2) │pies = 0 čevljev. (Takrat sonce pade navpično na glavo osebe).

-Ob 14. uri so porabili t = 8 ur:

S (8) = 6 │cot (π.8/12) │pies = 6 │cot (2π /3) │pies = 3.46 čevljev.

-Ko je 17:45, jih je 11 minilo 11.75 ur od 6. ure zjutraj, potem:

S (11.75) = 6 │cot (π x 11.75/12) │pies = 91.54 čevljev. V tem času sence postajajo daljše.

Ali lahko bralec izračuna čas, ko je senca osebe enaka njihovi višini?

Reference

1. Carena, m. 2019. Priročnik za matematiko prednavdljivosti. Nacionalna univerza na obali.
2. Figuera, j. 1999. Matematika. 1. Raznovrstno. Bolivarske kolegijske izdaje.
3. Hoffman, J. Izbira vprašanj matematike. Zvezek 4.
4. Jiménez, r. 2008. Algebra. Dvorana Prentice.
5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.