Stopnje funkcije, večje od dveh (primeri)

(Polinom) stopnje, večje od dveh, ima splošno obliko:

f (x) = a₀ + do₁x +a₂x² +.. .do_nxⁿ

Z n = 3, 4, 5,…, ne -negativno celo število in koeficienti_tudi, do₁… Do_n, ki so običajno resnične številke.

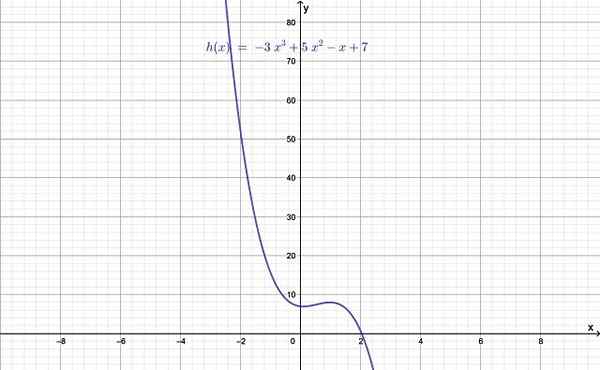Slika 1.- Graf stopinjske funkcije, večje od 2. Vir: f. Zapata.

Stopnja funkcije je podana z vrednostjo N, največjega od eksponentov in ki je večja od 2. Kadar je n = 0 konstantna funkcija, če je n = 1, je linearna funkcija in končno z n = 2 je kvadratna funkcija.

Primeri funkcij večjih od dveh v spremenljivki "x" so naslednji:

• f (x) = x³
• H (x) = - 3x³ + 5x² - X + 7
• g (x) = x⁴ - 6x² + 25

Funkcija f (x) = x³ Je najpreprostejša od vseh funkcij, večjih od dveh, njegova stopnja pa 3. Stopnja 3 je znana tudi kot Kubična funkcija. G (x) je 4 stopnje, saj je 4 največji eksponent.

Vrednost N je zelo pomembna, ker določa splošno obliko grafa in tudi največjo količino korenin ali križišč, ki jih ima funkcija z vodoravno osjo. Dejansko se bo funkcija 3 -grada dotaknila največ 3 točke vodoravne osi, ena od razredov 4 bo to storila največ v 4 točkah in tako naprej.

Kar zadeva neodvisni izraz, v polinomni funkciji katere koli stopnje označuje presečišče funkcije z navpično osjo.

Značilnosti polinomnih funkcij večjih od dveh

Domena

Domena funkcije je niz vrednosti, ki omogočajo izračun vrednosti y = f (x). Za polinomne funkcije je ta niz resničnih N številk ali nabora zapletenih številk, če je potrebno za razširitev domene.

Vam lahko služi: trigonometrične meje: kako jih rešiti, rešiti vaje

Pomeni, da glede na polinomno funkcijo f (x) = a₀ + do₁x +a₂x² +.. .do_nxⁿ, Vedno lahko zamenjate katero koli resnično številko, izvedete navedene operacije in kot rezultat pridobite vrednost resničnega y = f (x).

Domet

To je nabor, ki ga tvorijo vse pridobljene vrednosti F (x), to je slika, ki jih ima vsaka vrednost X prek funkcije f (x). Za polinomne funkcije, večje od 2, je ta sklop resničnih številk.

Korenine funkcije

So vrednosti x, za katere se izpolni, da je f (x) = 0. Kot je navedeno zgoraj, stopnja funkcije kaže na največje število korenin, ki jih lahko ima, čeprav niso vsi nujno resnični.

Ko so koeficienti funkcije realne številke, prave korenine ustrezajo presečiljem funkcije z osi x.

Primer 1

Racionalne korenine funkcije f (x) = 2x³ - 9x² + 7x + 6 najdete v naslednjem teoremu:

Če koren f (x) = a₀ + do₁x +a₂x² +.. .do_nxⁿ To je oblika b/c, zato so možne vrednosti B faktorji a_tudi in možne vrednosti c so dejavniki a_n.

Za funkcijo primera so že poenostavljene kombinacije: ± 6, ± 3, ± 2, ± 1, ± 3/2, ± ½. Zdaj se vsaka preizkusi s postopkom sintetične delitve, na primer. Ko je ostanek delitve 0, je dokazana vrednost korenina:

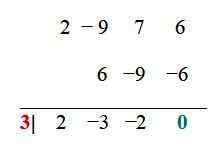
Vrednost x₁ = 3 je korenina ali nič funkcije, zato je (x - 3) pogost faktor f (x) in to je mogoče zapisati kot:

Lahko vam služi: enotni krog: trigonometrične funkcije in aplikacije

f (x) = (x - 3) ∙ (2x² −3x −2)

Preostali dve korenini sta vrednosti, ki izpolnjujejo enačbo 2x² −3x −2 = 0. To enačbo je mogoče rešiti s splošno formulo, znanstvenim kalkulatorjem ali ponovitvijo prejšnjega postopka Tanteo.

Te korenine so x₂ = 2 in x₃ = - ½, zdaj pa lahko F (x) zapišemo kot produkt treh dejavnikov:

f (x) = (x - 3) ∙ (x - 2) ⋅ (x + ½)

Križišča f (x) z osi x so točke: P₁ (3.0), str₂(2.0) in P₃(−½, 0). Graf funkcije, pridobljen z geogebro, prikazuje svoja križišča z osi x:

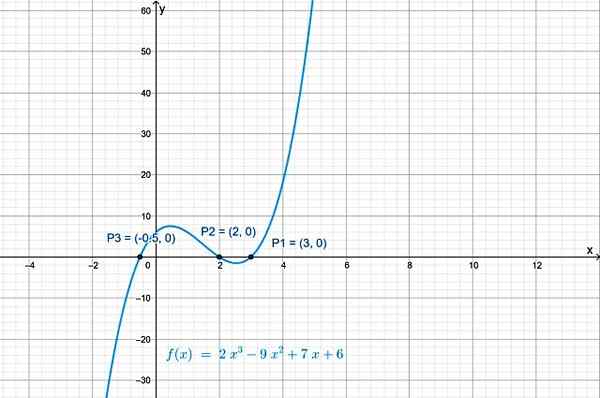Slika 2.- Polinomna funkcija stopnje 3 ima tri križišča z vodoravno osjo. Vir: f. Zapata.

Križišče z navpično osi

Če želite najti presečišče funkcije z navpično osi, morate najti F (0), kar je preprosto₀.

Primer 2

Poiščite presečišče f (x) = 2x³ - 9x² + 7x + 6 Z navpično osi je zelo preprost, pri izdelavi x = 0 v f (x) dobimo:

f (x) = 6

In presečišče funkcije z navpično osi je p₄(0,6).

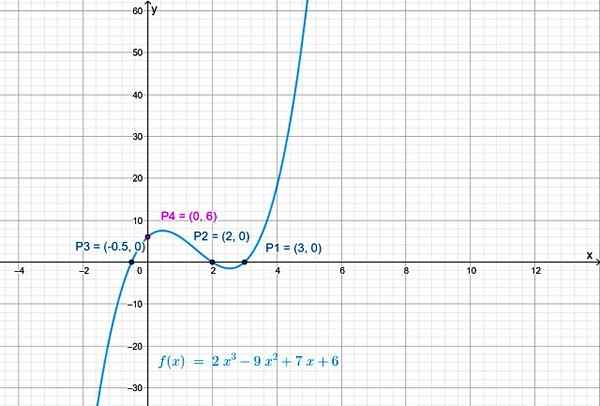Slika 3. Presečišče krivulje z navpično osi naredi x = 0 v f (x). Vir: f. Zapata.

Kontinuiteta

Polinomne funkcije na splošno, zlasti tiste, ki so višje od 2, so neprekinjene funkcije v celotni domeni, kar pomeni, da nimajo skokov, korakov, lukenj ali vrednot. Prav tako nimajo asimptote, ki so navpične, vodoravne ali poševne naravnost, na katere se približuje funkcija, ne da bi jih prečkali.

Te lastnosti mehkobe in kontinuitete so cenjene v zgoraj prikazanih grafih.

Graf funkcij višje od 2

Grafi funkcij višje od 2 so neprekinjeni in mehki, njihova oblika pa je odvisna od stopnje polinoma.

Vam lahko služi: permutacije brez ponovitve: formule, demonstracije, vaje, primeri

Na primer, tisti iz razreda 3. stopnje, ki imajo negativni znak v izrazu z najvišjo stopnjo).

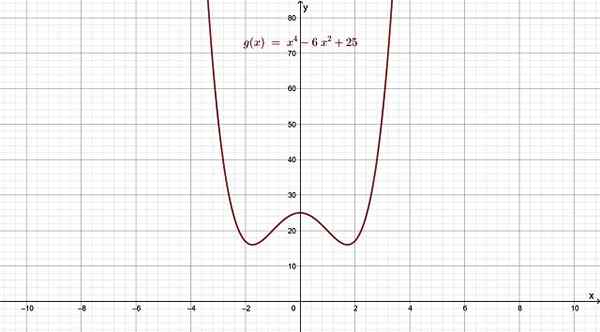Slika 4. Polinomna funkcija 4. stopnje, katerega graf spominja na črko W. Vir: f. Zapata.

Za vrednosti x stran od x = 0, levo in desno, funkcija se obnaša, kako bi to storil izraz največje stopnje, ker to prevladuje nad drugimi, ko X postane zelo velik ali zelo majhen.

Na sliki, ki sledi funkciji f (x) = 2x, primerjamo³ - 9x² + 7x + 6 s funkcijo r (x) = x³ In cenimo, da je oblika obeh krivulj podobna vrednosti x, ki so daleč od x = 0.

Pri velikih vrednostih X funkcija hitro raste tako, da se nagiba k +∞, medtem ko se za negativne vrednosti x funkcija hitro zmanjša in se nagiba k −∞.

Slika 5.- Vse funkcije razreda N se obnašajo podobno, ko se oddaljujejo od x = 0, levo in desno. Vir: f. Zapata.

Primerjava krivulj navora (slika 4) z nenavadno stopnjo (slika 2), če ima koeficient, ki spremlja izraz najvišjega razreda rastejo, medtem ko se tisti iz ciljne stopnje začnejo v "y" pozitivno in se zmanjšujejo.

Reference

1. Barnett, r. 2000. Predhodno: funkcije in grafika. 4. Izdaja. McGraw Hill.
2. Izračun.DC. Polinomne funkcije. Iztegnjeno od: izračun.DC.
3. Larson, r. 2012. Prekalenkulacija. 8. Izdaja. Cengage učenje.
4. Stewart, J. 2007. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
5. Varsity tutorrs. Grafiranje polinomnih funkcij. Pridobljeno iz: WarsityTorm.com.