Homografska funkcija, kako graditi, rešene vaje

The delovanjeHomografski ali racionalen Ón Gre za vrsto matematične funkcije, sestavljene iz delitve dveh polinomnih komponent. Upošteva obrazec P (x)/q (x), kjer Q (x) ne more imeti nobene oblike.

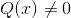
Na primer izraz (2x - 1)/(x + 3) ustreza homografski funkciji s p (x) = 2x - 1 y q (x) = x + 3.

Vir: Pixabay.com

Homografske funkcije so študijski del analitičnih funkcij, ki se obravnavajo iz grafičnega pristopa in iz študije domene in dosega. To je posledica omejitev in temeljev, ki jih je treba uporabiti za njihove resolucije.

[TOC]

Kaj je homografska funkcija?

So racionalni izrazi edinstvene spremenljivke, čeprav to ne pomeni, da ni podobnega izraza za dve ali več spremenljivk, kjer bi že bilo v prisotnosti teles v vesolju, ki ubogajo enake vzorce kot homografska funkcija v ravni.

V nekaterih primerih imajo resnične korenine, vendar se vedno vzdržuje obstoj navpičnih in horizontalnih asimptote. Običajno je prisoten le eden od teh trendov, vendar obstajajo izrazi, ki se lahko prikažejo v svojem razvoju.

Njegovo domeno omejujejo korenine imenovalca, ker med ničlo realnih številk ni delitve.

Mešana homografska funkcija

V izračunu so zelo pogosti, zlasti diferencialni in obsežni, saj so potrebni za izpeljavo in anti -angel pod določenimi formulami. Nekateri najpogostejši so razvrščeni spodaj.

N. Par homografske funkcije

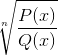
Izključuje vse elemente domene, zaradi katerih argument negativno. Korenine, ki so prisotne v vsakem polinomu, kažejo ničelne vrednosti, ko jih ocenijo.

Te vrednosti sprejemajo radikalno, čeprav je treba upoštevati temeljno omejitev homografske funkcije. Kjer Q (x) ne more prejeti ničelnih vrednosti.

Vam lahko služi: transcendentne funkcije: vrste, definicija, lastnosti, primeri

Rešitve intervalov je treba prestreči:

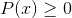
Za doseganje križišč je mogoče med drugim uporabiti metodo znaka.

Logaritem homografske funkcije

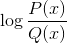
Izključuje vrednosti domene, ki mečejo negativne intervale in ničle. Ker so ničle že izključene iz imenovalca, rešitve: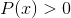

Običajno je tudi, da v enem najdemo oba izraza, med drugimi možnimi kombinacijami.

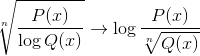
Kako graditi homografsko funkcijo?

Homografske funkcije grafično ustrezajo hiperbolam v ravnini. Ki se prevažajo vodoravno in navpično glede na vrednosti, ki definirajo polinome.

Obstaja več elementov, ki jih moramo določiti, da graficiramo racionalno ali homografsko funkcijo.

Posestvo

Prva bodo korenine ali ničle funkcij P in Q.

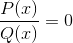
Dosežene vrednosti bodo označene na osi x grafike. Označevanje presečišč grafa z osi.

Navpična asimptota

Ustrezajo navpičnim črtam, ki razvajajo graf glede na trende, ki jih predstavljajo. Dotaknejo se osi x v vrednostih, zaradi katerih je imenovalec nič in se ga graf homografske funkcije nikoli ne bo dotaknil.

Vodoravna asimptota

Zastopana z vodoravno črto šiva, je razmejena meja, za katero funkcija ne bo določena na točno točki. Trendi bodo opaženi pred in po tej vrstici.

Za izračun se moramo zateči k metodi, podobni metodi l'Oup, ki se uporablja za reševanje racionalnih funkcij, ki se nagibajo k neskončnosti. Koeficiente najvišjih sil v števcu in imenovalec funkcije je treba vzeti.

Na primer, naslednji izraz ima vodoravno asimptoto pri y = 2/1 = 2.

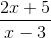
Interval rasti

Vrednosti naročenega bodo imele trende, označene v grafu zaradi asimptote. V primeru rasti se bo funkcija povečala od vrednosti, ko bodo elementi domene od leve proti desni ocenjeni.

Vam lahko služi: 60 delitev

Zmanjšanje intervala

Naročene vrednosti se bodo znižale, ko se ocenjujejo elementi domene od leve proti desni.

Skoki, ki jih najdemo v vrednostih, ne bodo upoštevani kot povečanje ali zmanjšanje. To se zgodi, ko je graf blizu navpične ali horizont.

Križišče z y

Če nič vrednost x, je križišče z osjo ordinat. To je zelo koristno dejstvo za pridobivanje grafa racionalne funkcije.

Primeri

Določite graf naslednjih izrazov, poiščite njegove korenine, navpične in vodoravne asimptote, rast in zmanjšanje intervalov in presečišča z osjo urejene os.

Vaja 1

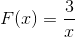
Izraz nima korenin, ker ima v števcu konstantno vrednost. Omejitev, ki jo je treba uporabiti, bo X razlikuje od ničle. Z vodoravno asimptoto pri y = 0 in asimptoto navpično pri x = 0. Z osi ni točk presečišča in.

Opazimo, da ni intervalov rasti, tudi če skok iz manj do bolj neskončnega v x = 0.

Interval zmanjšanja je

Id: (-∞; o) u (0, ∞)

Vaja 1.2

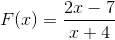
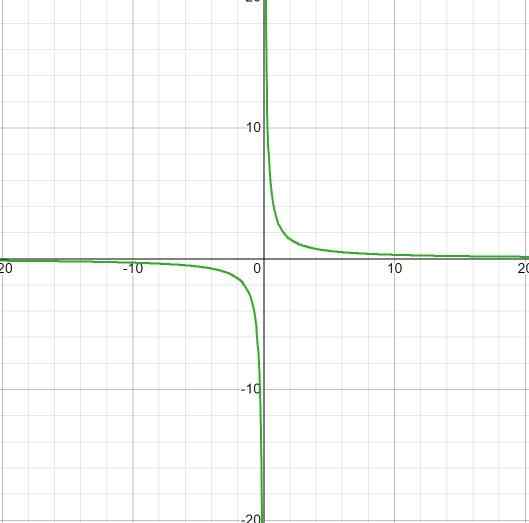
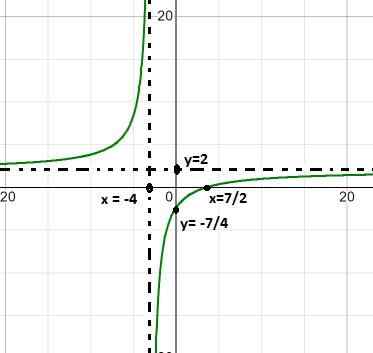
2 polinoma opazimo kot v začetni definiciji, zato nadaljujemo v skladu z uveljavljenimi koraki.

Najdeni koren je x = 7/2, kar je posledica izenačevanja funkcije.

Vertikalna asimptota je pri x = - 4, kar je vrednost, izključena iz domene zaradi racionalnega stanja funkcije.

Vodoravna asimptota je v y = 2, to po delitvi 2/1 koeficienti spremenljivk stopnje 1.

Ima križišče s tistimi, ki so bili naročeni pri y = - 7/4. Vrednost, ki jo najdemo po izenačevanju x do ničle.

Lahko vam služi: frakcija, enakovredna 3/5 (rešitev in razlaga)

Funkcija nenehno raste, s skokom iz več do manj neskončnega okoli korena x = -4.

Njegov interval rasti je (-nant, - 4) U ( - 4, ∞).

Ko je vrednost x blizu manj neskončne, funkcija prevzame vrednosti blizu 2. Enako se zgodi, ko se x približa bolj neskončno.

Izraz se približuje bolj neskončno, če ga ocenimo v - 4 na levi in ​​manj neskončno, če ga ocenimo v - 4 na desni.

Vaja 2

Opazimo graf naslednje homografske funkcije:

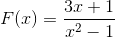
Opišite njihovo vedenje, korenine, navpične in vodoravne asimptote, intervale rasti in zmanjševanje in presečišče z urejeno osi.

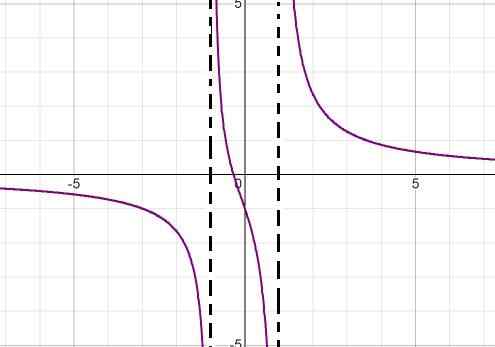
Ekspresijski imenovalec označuje z upoštevanjem razlike kvadratov (x + 1) (x - 1) vrednosti korenin. Na ta način lahko obe navpični asimptoti opredelimo kot:

x = -1 in x = 1

Vodoravna asimptota ustreza osi abscisa, ker je glavna moč v imenovalcu.

Njegov edini koren je opredeljen z x = -1/3.

Izraz se vedno zmanjšuje od leve proti desni. Ko se nagiba k neskončnosti, se približa nič. Manj neskončno, ko se približamo -1 na levi strani. Bolj neskončno, ko se približujete -1 na desni strani. Manj neskončno, ko se približujete 1 na levi in ​​več neskončnosti, ko se približate 1 na desni.

Reference

1. Približek z racionalnimi funkcijami. Donald J. Newman. Ameriški matematični Soc., 31. decembra. 1979
2. Funkcije ortogonalnih ocen. Univerza v La Laguna Tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13. februar. 1999
3. Približek resničnih funkcij. Str. Str. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. marca. 2011
4. Algebrske funkcije. Gilbert Ames Bliss. Couer Corporation, 1. januar. 2004
5. Revija španske matematične družbe, 5-6 zvezkov. Špansko matematično društvo, Madrid 1916