Funkcija stalnih značilnosti, primeri, vaje

The konstantna funkcija Je tisto, v katerem vrednost in. Z drugimi besedami: konstantna funkcija ima vedno obrazec  f (x) = k, kje k To je resnično število.

Z grafiko konstantne funkcije v koordinatnem sistemu Xy, Vedno je ravna črta vzporedna z vodoravno os ali osjo x.

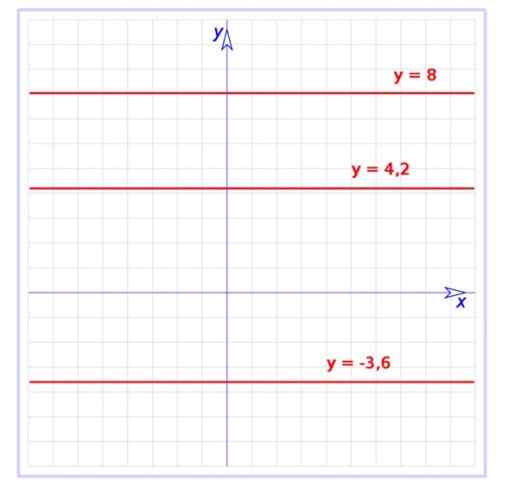
Slika 1. Graf več stalnih funkcij na kartezijanski ravnini. Vir: Wikimedia Commons. Uporabnik: hite [javna domena]

Ta funkcija je poseben primer povezana funkcija, čigar graf je tudi ravna črta, vendar z naklonom. Konstantna funkcija je v teku ničelna, to je horizontalna črta, kot je prikazano na sliki 1.

Obstaja graf treh stalnih funkcij:

f (x) = -3.6

G (x) = 4.2

H (x) = 8

Vsi so naravnost vzporedni z vodoravno osi, prva je pod osi, preostali pa so zgoraj.

[TOC]

Značilnosti konstantne funkcije

Glavne značilnosti konstantne funkcije lahko povzamemo na naslednji način:

-Njegov graf je vodoravna ravna črta.

-Ima edinstveno križišče z osi in, Vredno k.

-Je neprekinjeno.

-Obvladovanje konstantne funkcije (niz vrednosti, ki x) je niz realnih številk R.

-Pot, domet ali protislovje (nabor vrednosti, ki jih spremenljivka vzame in) je preprosto stalnica k.

Primeri

Funkcije so potrebne za vzpostavitev povezav med velikostmi, ki so na nek način odvisne drug od drugega. Obstoječi odnos med njimi je mogoče matematično modelirati, da vemo, kako se eden od njih obnaša, ko se drugi razlikuje.

Vam lahko služi: papomudas

To pomaga pri gradnji modelov za številne situacije in napoveduje njihovo vedenje in evolucijo.

Kljub svoji navidezni preprostosti ima stalna funkcija veliko aplikacij. Na primer, ko gre za študij velikosti, ki ostanejo konstantne v času, ali vsaj za opazen čas.

Na ta način se magnitude obnašajo v situacijah, kot so naslednje:

-The hitrost Križarjenje avtomobila, ki se premika po dolgi pravokotni avtocesti. Dokler se ne ustavi ali pospeši, avtomobil nosi enotno pravokotno gibanje.

Slika 2. Če se avtomobil ne ustavi ali pospeši, ima enakomerno pravokotno gibanje. Vir: Pixabay.

-Popolnoma naložen in odklopljen kondenzator iz vezja ima breme konstantno v času.

-Končno parkiranje pavšalnega cena vzdržuje a cena ne glede na to, kako dolgo je tam parkiran avtomobil.

Drug način za predstavljanje konstantne funkcije

Konstantna funkcija je lahko predstavljena na naslednji način:

f (x) = kx⁰

Ker kakršna koli vrednost x Povišano na 0 daje 1, kot rezultat, prejšnji izraz se zmanjša na znano:

f (x) = k

Seveda to se zgodi, dokler vrednost k je drugačen od 0.

Zato je konstantna funkcija razvrščena tudi kot a polinomna funkcija stopnja 0, saj je eksponent spremenljivke x Je 0.

Rešene vaje

- Vaja 1

Odgovorite na naslednja vprašanja:

a) Ali je mogoče potrditi, da je črta, ki jo daje x = 4? Razlog za vaš odgovor.

b) Ali ima konstantna funkcija presečišče z osi x?

c) je funkcija f (x) = w konstanta²?

Odgovor na

Tu je graf vrstice x = 4:

Vam lahko služi: statistične spremenljivke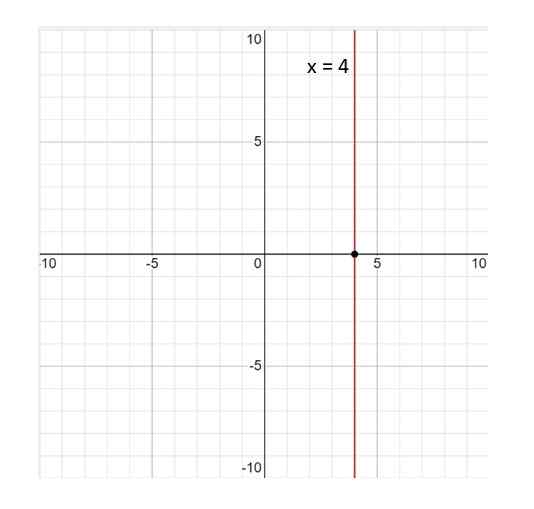 Slika 3. Graf vrstice x = 4. Vir: f. Zapata.

Vrstica x = 4 ni funkcija; Po definiciji je funkcija odnos tako, da za vsako vrednost spremenljivke x Ustreza eni vrednosti in. In v tem primeru to ni izpolnjeno, saj vrednost x = 4 je povezan z neskončnimi vrednostmi in. Zato je odgovor ne.

Odgovor b

Na splošno konstantna funkcija nima presečišča z osi x, razen če je y = 0, V tem primeru gre za os x Pravilno rečeno.

Odgovor c

Ja, od W Je konstantna, tudi njen kvadrat je. Kakšne interese je to W Ni odvisno od vhodne spremenljivke x.

- Vaja 2

Poiščite križišče med funkcijami f (x) = 5 in G (x) = 5x - 2

Rešitev

Če želite najti presečišče med tema dvema funkcijama, jih je mogoče prepisati kot:

y = 5; y = 5x - 2

Ujemajo se in pridobivajo:

5x - 2 = 5

Ki je linearna enačba prve stopnje, katere rešitev je:

5x = 5+2 = 7

x = 7/5

Točka križišča je (7/5; 5).

- Vaja 3

Dokazujte, da je tisti, ki izhaja iz stalne funkcije, 0.

Rešitev

Iz definicije derivata imate:

 f (x) = k

f (x+h) = k

Nadomestitev definicije:

Zgoraj je smiselno, saj je derivat funkcije opredeljen kot naklon črte tangenta do krivulje v dani točki. Konstantna funkcija ima v teku ničelno in tudi katero koli tangentno linijo.

Poleg tega, če razmišljamo o derivatu kot tečaju Dy/dx, Konstantna funkcija ne doživi nobene spremembe, zato je njegov izpeljan ničen.

Lahko vam služi: Multiplikativno načelo: Tehnike štetja in primeri

- Vaja 4

Poiščite nedoločen integral f (x) = k.

Rešitev

- Vaja 5

Podjetje za mobilni telefon ponuja neomejeno internetno storitev s pavšalno ceno, ki plačuje 15 USD na mesec. Kakšna je cenovna funkcija glede na čas?

Rešitev

Naj bo P cena, ki jo je treba plačati v času $ in T, kar je mogoče izraziti v dneh. Funkcija je vzpostavljena na naslednji način:

P (t) = 15

- Vaja 6

Naslednji graf v primerjavi s časovnim časom ustreza gibanju delca.

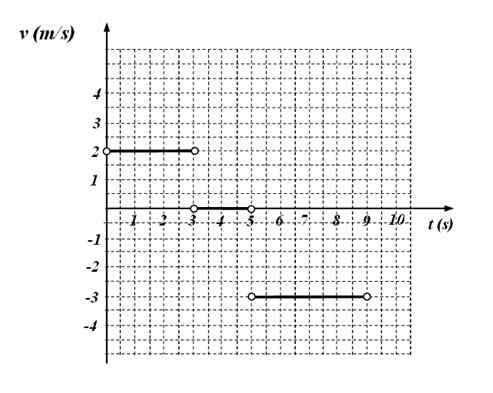Slika 4. Funkcija V (t) Graf funkcije za vadbo 6. Vir: f. Zapata.

Zahteva se:

a) Napišite izraz za funkcijo hitrosti kot funkcijo časa V (t).

b) Poiščite razdaljo, ki jo mobilni telefon prevozi v časovnem intervalu med 0 in 9 sekundami.

Rešitev

Grafa, ki prikazuje, da:

-V = 2 m/s V časovnem intervalu med 0 in 3 sekundami

-Mobilni telefon je pridržan med 3 in 5 sekundami, saj je v tem intervalu hitrost vredna 0.

-V = - 3 m/s Med 5 in 9 sekundami.

Je primer kosa kosov ali funkcije v delih, ki je sestavljen iz stalnih funkcij, ki veljajo samo za navedene časovne intervale. Ugotovljeno je, da je iskana funkcija:

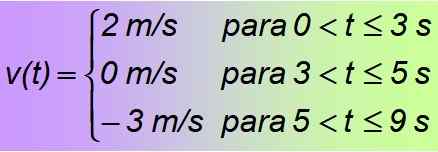
Rešitev b

Iz grafa V (t) je mogoče izračunati razdaljo, ki jo prevozi mobilni telefon, kar je številčno enaka območju nizko/na krivulji. Na ta način:

-Razdalja je prevozila med 0 in 3 sekunde = 2 m/s . 3 s = 6 m

-Med 3 in 5 sekundami so ga pridržali, zato ni prehodil nobene razdalje.

-Razdalja je prevozila med 5 in 9 sekundami = 3 m/s . 4 s = 12 m

Skupaj je mobilni telefon gostoval 18 m. Glej, da čeprav je hitrost v intervalu med 5 in 9 sekundami negativna, je prevožena razdalja pozitivna. Kar se zgodi, je, da je v tem časovnem intervalu mobilni telefon spremenil pomen svoje hitrosti.

Reference

1. Geogebra. Stalne funkcije. Okreval od: geogebra.org.
2. Maplesoft. Konstantna funkcija. Okrevano od: Maplessoft.com.
3. Wikilibros. Izračun v spremenljivki/funkcijah/konstantni funkciji. Okrevano od: je.Wikibooks.org.
4. Wikipedija. Konstantna funkcija. Pridobljeno iz: v.Wikipedija.org
5. Wikipedija. Konstantna funkcija. Okrevano od: je.Wikipedija.org.