Formule centrifugalne sile, kako izračunane, primeri, vaje

The centrifugalna sila ponavadi izrine telesa, ki se obrnejo na krivuljo. Velja za eno izmišljena sila, pseudofuerza tudi inercialna sila, Ker ga ne povzročajo interakcije med resničnimi predmeti, ampak je manifestacija Inercija trupla. Inercija je lastnost, zaradi katere predmeti želijo ohraniti počitek ali enotno pravokotno gibanje, če jo imajo.

Izraz "centrifugalna sila" je skoval znanstvenik Christian Huygens (1629-1695). Potrdil je, da bi jih krivulinearno gibanje planetov odmaknilo, razen če sonce ne bi imelo sile, da bi jih obdržalo, in izračunal, da je ta sila sorazmerna s kvadratom hitrosti in obratno sorazmerna s polmerom opisanega oboda.

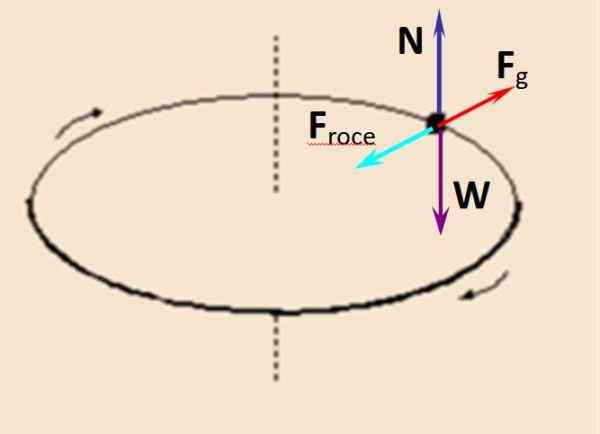
Slika 1. Ko dajejo krivuljo, potniki doživijo silo, ki jih ponavadi izvleče. Vir: LibreShot.

Za tiste, ki potujejo po avtomobilu, centrifugalna sila sploh ni fiktivna. Potniki avtomobila, ki se obrne na desno, se počutijo v levi in ​​obratno, ko se avtomobil obrne v levo, ljudje doživijo silo na desno, kar se zdi.

Velikost centrifugalne sile F_g Izračuna se z naslednjim izrazom:

 Kje:

-F_g To je velikost centrifugalne sile

-m To je masa predmeta

-v Je hitrost

-R To je polmer ukrivljene poti.

Sila je vektor, zato se za razlikovanje od njegove razsežnosti uporablja krepka črka, ki je skalar.

Vedno moraš imeti v mislih, to F_g se pojavi le, ko je gibanje opisano z uporabo pospešenega referenčnega sistema.

V primeru, opisanem na začetku, ogled, ki se vrti, pomeni pospešeno referenco, saj zahteva centripetalni pospešek, tako da se lahko obrnem.

[TOC]

Kako se izračuna centrifugalna sila?

Izbira referenčnega sistema je ključnega pomena za spoštovanje gibanja. Pospešeni referenčni sistem je znan tudi kot neinarcijski sistem.

V tej vrsti sistema, kot avtomobil, ki se vrti, se pojavljajo izmišljene sile, kot je centrifugalna sila, katerih izvor ni prava interakcija med predmeti. Potnik ni mogel povedati, kaj ga potisne iz krivulje, lahko samo potrdi, kaj se zgodi.

Po drugi strani so v inercialnem referenčnem sistemu interakcije med resničnimi predmeti, kot sta telo v gibanju in zemlja, kar ima za posledico telesno težo, ali med telesom in površino, na katerem se giblje, kar izvira normalno.

Opazovalec, ki stoji na robu ceste in kdo zagleda avto, da daje krivuljo, je dober primer inercialnega referenčnega sistema. Za tega opazovalca se avtomobil vrti, ker deluje silo, usmerjeno proti sredini krivulje, kar ga prisili, da se ne izvleče iz njega. Gre za centripetalna sila, ki nastane s trenjem med pnevmatikami in pločnikom.

V inercialnem referenčnem sistemu se centrifugalna sila ne pojavi. Zato je prvi korak za izračun, da natančno izberete referenčni sistem, ki bo uporabljen za opis gibanja.

Lahko vam služi: občutljiva toplota: koncept, formule in vaje rešene

Nazadnje je treba opozoriti, da inercialni referenčni sistemi ne bi smeli nujno biti v mirovanju, na primer opazovalec, ki pogleda vozilo, da bi dal krivuljo. Inercialni referenčni sistem, znan kot Laboratorijski referenčni okvir, Lahko je tudi v gibanju. Seveda s konstantno hitrostjo glede inercialne.

Brezplačni karoserijski diagram v inercialnem in neresničnem sistemu

Na naslednji sliki na levi strani opazovalec ali stoji in pogleda O ', ki je na ploščadi, ki se vrti v navedeni smeri. Za O, ki je inercialni okvir, zagotovo ali 'se vzdržuje z obračanjem zaradi centripetalne sile F_c proizveden z mrežno steno na zadnji strani o '.

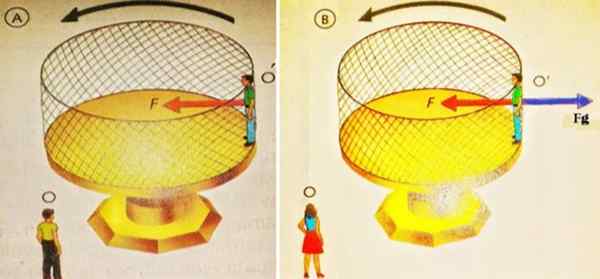Slika 2. Oseba, ki stoji na vrtljivi ploščadi, je razvidna iz dveh različnih referenčnih sistemov: enega fiksnega in tistega, ki gre z osebo. Vir: Santillana Physics.

Samo v inercialnih referenčnih sistemih je veljavno uporabiti Newtonov drugi zakon, ki navaja, da je neto sila s pospeševanjem enak produktu mase. In pri tem se s prikazanim diagramom prostega telesa dobi:

F_c = ma_c

F_c= MV² / R

Podobno je na pravi sliki tudi prosti diagram telesa, ki opisuje, kaj opazovalec vidi ali '. S svojega vidika je v mirovanju, zato so sile na njem uravnotežene.

Te sile so: normalno F, da stena na njej, v rdeči barvi in ​​usmerjena proti sredini in centrifugalni sili F_g To ga izrine in ki ne izvira iz nobene interakcije, je ne-avtilna sila, ki se v referenčnih sistemih pojavi v rotaciji.

Centrifugalna sila, ki je fiktivna, uravnoteži resnična sila, stik ali normalna sila, ki kaže na središče. Zato:

∑f_x = 0 → F_g - F = 0

F_g = F

Primeri

Čeprav se centrifugalna sila šteje za psevdo -frecking, so njegovi učinki povsem resnični, kot je razvidno iz naslednjih primerov:

- V kateri koli vrtljivi igri zabaviščnega parka je prisotna centrifugalna sila. Skrbi, da "pobegnemo od središča" in nudi stalen odpor, če poskušate stopiti proti središču premikajočega se vrtiljaka. Na naslednjem nihalu si lahko ogledate centrifugalno silo:

Vam lahko služi: Eugen Goldstein: Biografija, prispevki in odkritja

https: // giphy.com/gifs/jtu3pnmkqomqdujwmo

- Učinek Coriolisa izhaja iz kopenskega vrtenja, zaradi česar je zemlja prenehala inercialni okvir. Potem se pojavi sila Coriolis, da psevdo sila, ki stransko preusmeri predmete, kot pri ljudeh, ki poskušajo hoditi po vrtljivi ploščadi.

https: // giphy.com/gifs/the-x-files-sully-mulder-funlgylkhobs

Vaje

Vaja 1

Avtomobil, ki se vrti s pospeševanjem Do Na desni nosi nagačeno igračo, ki visi z notranjega vzvratnega ogledala. Narišite in primerjajte diagrame telesa brez igrač iz:

a) inercialni referenčni okvir opazovalca, ki stoji na cesti.

b) potnik, ki potuje v avtu.

Rešitev

Opazovalec, ki stoji na cesti, opozarja, da se igrača hitro premika s pospeševanjem Do na desno.

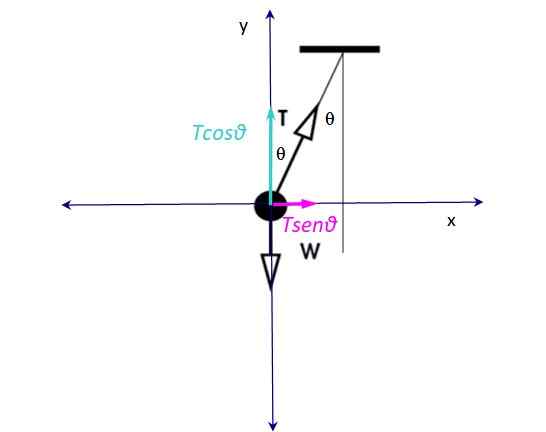Slika 3. Brezplačni karoserijski diagram za vajo 1A. Vir: f. Zapata.

Na igrači delujeta dve sili: na eni strani napetost v vrvi T in navpična teža navzdol W. Teža je uravnotežena z navpično komponento napetosti TCOSθ, Zato:

W - tcosθ = 0

Vodoravna komponenta napetosti: T. Senθ To je neuravnotežena sila, ki je odgovorna za pospešek na desni, zato je centripetalna sila:

F_c= T.Senθ = ma_c

Rešitev b

Za potnika v avtomobilu igrača visi v ravnovesju in diagram je naslednji:

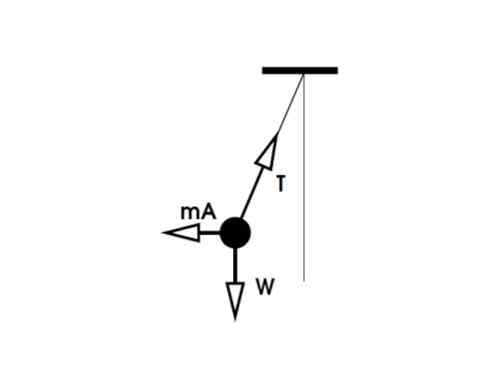Slika 4. Brezplačni karoserijski diagram za vajo 1b. Vir: f. Zapata.

Tako kot v prejšnjem primeru se teža in navpična komponenta napetosti kompenzirata. Toda vodoravna komponenta je uravnotežena s fiktivno silo F_g = ma, tako da:

-ma + tsenθ = 0

F_g = ma

Vaja 2

Valuta je na robu starih vinilnih nalog, katerih polmer je 15 cm in se vrti s hitrostjo 33 vrtljajev / minuto. Poiščite minimalni statični koeficient trenja, potreben za vzdrževanje valute, z valuto valute.

Rešitev

Na sliki je diagram prostega telesa za opazovalca, ki se premika z valuto. Normalno N da toadiscos izvaja navpično navzgor, se uravnoteži s težo W, medtem ko centrifugalna sila F_g je kompenzirano s statičnim drgnjenjem F_dotik.

Slika 5. Brezplačen diagram telesa za vadbo 2. Vir: f. Zapata.

N - w = 0

F_dotik - F_g = 0

Obseg centrifugalne sile je MV²/R, Kot je navedeno na začetku, potem:

F_dotik = F_g = MV²/R

Po drugi strani je statična trenja dana:

Vam lahko služi: volt ali volt: koncept in formule, enakovrednosti, primeri

F_{Reco =} μ_s.N

Kje μ_s To je statični koeficient drgnjenja, sproščena količina, katere vrednost je odvisna od tega, kako so površine v stiku. Zamenjava te enačbe ostaja:

μ_s.N = mv²/R → μ_s = MV²/R.N

Treba bi določiti velikost običajnega, ki je povezana s težo v skladu z n = mg. Znova zamenjava:

μ_s = MV²/R.mg → μ_s = v²/Rg

Nazaj na izjavo, to poroča, da se valuta vrti s hitrostjo 33 revolucij /minute, kar je kotna hitrost ali kotna frekvenca Ω, povezano z linearno hitrostjo v:

v = ω.R = 33 Rev/min . 2π Radianes/Rev . 15 cm . (1 min/60 s) = 51. 8 cm/s

μ_s = v²/Rg = (51.8 cm/s)²/ (15 cm x 981 cm/ s²) = 0.18

Rezultati te vaje bi bili enaki, kot če bi izbrali inercialni referenčni sistem. V tem primeru je edina sila, ki lahko izvira pospeševanje proti sredini, statičen dotik.

Prijave

Kot pravimo, je centrifugalna sila fiktivna sila, ki se ne pojavlja v inercialnih okvirih, ki so edini, v katerih so Newtonovi zakoni veljavni. V njih je centripetalna sila odgovorna za zagotavljanje telesa s potrebnim pospeševanjem proti sredini.

Centripetalna sila ni drugačna sila že znanega. Nasprotno, prav to, ki opravljajo vlogo centripetalnih sil, kadar je to primerno. Na primer gravitacija, ki naredi luno orbito.

Vendar pa, ko je veliko pospešenih referenčnih sistemov, imajo izmišljene sile zelo resnične učinke. Za vzorec so tukaj tri pomembne aplikacije, v katerih imajo oprijemljive učinke:

Centrifugatorji

Centrifugatorji so široko uporabljeni instrumenti v laboratoriju. Ideja je, da se mešanica snovi obrne z veliko hitrostjo in tiste snovi z večjo maso, doživite večjo centrifugalno silo, v skladu z enačbo, opisano na začetku.

Potem se bodo najbolj masivni delci oddaljili od osi vrtenja in se tako ločili od najlažjega, kar bo ostalo bližje središču.

Pralni stroji

Samodejni pralni stroji imajo različne cikle stiskanja. V njih so oblačila centrifugirana za odpravo preostale vode. Več revolucij cikla, manj mokre bodo oblačila na koncu pranja.

Krivulja peralte

Avtomobili se bolje sprejmejo na cestah, zahvaljujoč se cesti, ki se nekoliko nagne proti središču krivulje, kar je znano kot Peralte. Na ta način avtomobil ni odvisen izključno od statičnega trenja med pnevmatikami in cesto, da dokončate zavoj, ne da bi zapustili krivuljo.

Reference

1. Acosta, Victor. Gradnja didaktičnega vodnika na centrifugalni sili za študente cikla v 10. razred.Okrevano od: bdigital.a i.Edu.co.
2. Toppr. Zakoni gibanja: gibanje okrožnice. Okrevano od: toppr.com.
3. Resnick, r. (1999). Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
4. Avtonomna univerza v zvezni državi Hidalgo. Centrifugalna sila. Okreval od: uaeh.Edu.mx
5. Wikipedija. Centrifugatorji. Okrevano od: je.Wikipedija.org.