Frakcije, enakovredne 3/4

The Frakcije, enakovredne 3/4 So tisti, v katerih z delitvijo števca med imenovalcem ima za posledico decimalno številko 0.75.

Vedno je mogoče. Če je rezultat te operacije enak 0.75, delček je enakovreden 3/4, na primer del 6/8:

Delež 6/8 je enakovreden ¾, saj z delitvijo števca med imenovalcem v obeh primerih 0 dobimo 0.75. Vir: f. Zapata.

Zdaj smo dobili frakcijo 6/8 z množenjem števca in ¾ imenovalca. S hkrati pomnožitvijo števca in imenovalca z isto količino decimalna vrednost določenega frakcije ni spremenjena, ampak omogoča pridobivanje frakcij, ki so enakovredni danemu.

Drug način, da najdete delček, enakovreden drugemu. Vendar v primeru ¾ ni mogoče najti takšne številke, ki se hkrati deli na 3 in 4, rezultat pa je celo število. To je zato, ker sta 3 in 4 bratranca med seboj, zato nimata skupnih delitev.

Ko sta števca in imenovalec delčka glavnih številk drug z drugim, je rečeno, da je delček nereducibilno. Zato je ¾ neprekinjeno.

Načine, kako najti delček, ki ustreza drugemu

Obstajata dva zelo preprosta načina, kako najti frakcijo, enakovredni drugi dani del: Prvi je z redukcijo, drugi pa z ojačitvijo.

Zmanjšanje in ojačanje ulomkov

Zmanjšanje

Ta postopek je sestavljen iz iskanja števila, ki je delitelj tako števca kot imenovalca. Ko so ga našli, sta števca in imenovalec razdeljena s to vrednostjo in takoj dobita delček, ki ustreza izvirniku. Preverjeno je, da tako dela številčno razmerje med imenovalcem in primerjanjem.

Vam lahko služi: matematične funkcije

Ko je nepoučen del drugega. Tako pridobljena frakcija je neprebujena.

Frakcija ¾ je nepopustljiva, kot je navedeno prej, za 3 in 4 bratrance med seboj, naslednja metoda.

Ojačitev

Za povečanje določenega deleža je treba števca in imenovalec pomnožiti z istim zneskom, ne glede na to, ali gre za pozitivno ali negativno število. Na primer, delež 6/8 smo dobili z ojačitvijo ¾ s faktorjem 2:

Čeprav imajo frakcije drugačnega štetja in imenovalca, sta oba enaka.

Upoštevajte naslednjo sliko, ki vsebuje dva enaka kroga, razdeljena na enake dele, čeprav različnih velikosti. Previdno opazovanje, območja v zeleni in vijolični barvi imajo enak ukrep, vendar je zeleno območje razdeljeno na 3 dele, od 4 skupaj, ki sestavljajo krog levice. Po drugi strani je bil krog desno razdeljen na 8 enakih delov in vijolično območje je enakovredno 6.

Na ta način lahko gravite, da je ¾ enakovreden 6/8, saj obe frakciji predstavljata enak znesek.

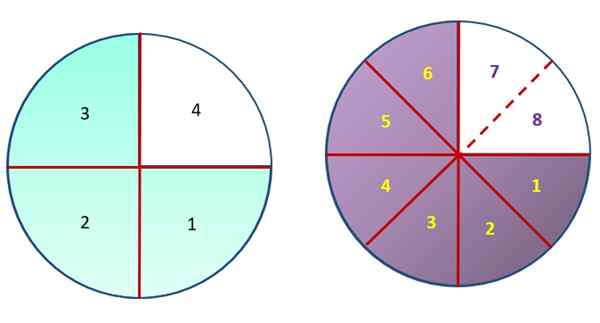Frakcije ¾ in 6/8 predstavljata isto območje v obeh krogih. Vir: f. Zapata.

Na splošno, če se frakcija pomnoži ¾ po številu n, se toliko frakcij, enakovrednih temu, dobijo, kot želite:

Pomembno je opozoriti, da n nikoli ne more biti enak 0, saj delitev z 0 ni definirana. Noben delček ne more imeti 0 v vašem imenovalcu.

Kako vedeti, ali je del enakovreden 3/4?

Kot je razloženo na začetku, je način vedenja, ali je delček enakovreden ¾. Če je 0.75, delček je enakovreden ¾, vendar je treba vedeti še nekaj metod, ki ne potrebujejo neposredno delitve:

Lahko vam služi: tehtani mediji: kako se izračuna, primeri in vaje

Metoda 1

Recimo, da frakcija A/B, in želite vedeti, ali je enakovreden ¾, to je, če je res, da:

Če želite biti enakovreden, mora biti izdelek 4 enak izdelku 3B:

4a = 3b

Metoda 2

Če je frakcija A/B enaka ¾, delitev A in B z največjim skupnim delilnikom MCD, mora biti rezultat ¾.

Če želite razjasniti uporabo teh metod, glejte naslednje primere.

Primeri

Primer 1

Ugotovite, ali je delež 150/200 enakovreden ¾:

Po metodi 1

V tem primeru A = 150 in B = 200 je treba izpolniti:

4a = 3b

• 4 × 150 = 600
• 3 × 200 = 600

Ugotovljeno je, da je 150/2 enakovredno ¾.

Po metodi 2

Največji skupni delitelj 150 in 300 jih natančno deli. Obe količini se razgrajujeta v svojih glavnih dejavnikih, nato pa se pomnožijo skupni dejavniki z najmanjšim eksponentom:

• 150 = 2 × 5² × 3
• 200 = 2³ × 5²

2 in 5 sta pogosta, pomnožita najmanj moči, s katero se pojavljata:

MCD (150, 200) = 2 × 5² = 2 × 25 = 50

Zdaj nadaljujemo z delitvijo:

Rešene vaje

Vaja 1

Napišite z amplifikacijo pet frakcij, enakovrednih ¾, pomnoži števce in imenovalca vsakič z naslednjimi celotnimi številkami:

a) 3, b) 5, c) (-2), d) 10 in e) 20

Rešitev

Rešitev b

Rešitev c

Upoštevajte, da ni nobene razlike z ojačanjem frakcije za 2 ali -2, saj je v skladu s pravilom znakov količnik, naveden med dvema negativnima količinama.

Rešitev d

Rešitev e

Upoštevajte, da je ta frakcija enaka, kot jo dobimo z ojačitvijo za 2 zgoraj navedeni delež:

Vaja 2

Preverite, ali so naslednji frakciji enakovredni ¾:

Lahko vam služi: pravokotne koordinate: primeri in vaje rešene

a) 18/24; b) 21/28; c) 24/32; d) 27/38; e) 33/44

Rešitev

Z uporabo zgoraj opisane metode 1:

4a = 3b

Za frakcijo 18/24 morate = 18 in B = 24, potem:

• 4 × 18 = 72
• 3 × 24 = 72

Zato sta 18/24 in 3/4 enakovredna.

Rešitev b

V skladu z metodo 2 moramo najti največji skupni delitelj (MCD) 21 in 28, nato deliti oba z rezultatom, in če dobimo frakcijo 3/4, so enakovredni:

21 = 3 × 7
28 = 4 × 7 = 2²× 7

Skupni faktor je 7, torej MCD (21,28) = 7, potem:

Rešitev c

Za to vajo se preveri, ali je količina med 24 in 32 0 0.75:

24 ÷ 32 = 0.75

Nato je 24/32 enakovreden 3/4.

Rešitev d

V frakciji 27/38 opazimo, da 38 ni večkratnik 4, zato ni enakovreden 3/4. Kakorkoli že, razvijanje med 27 in 38 se izvaja:

27 ÷ 38 = 0.710526

Od tega je ugotovljeno, da 27/38 ni enakovredno 3/4.

Rešitev e

Zlahka je razvidno, da se frakcija 33/44 pridobi z množenjem števca in imenovalca 3/4 do 11, kot je ta:

Zato so enakovredni.