Pretok električnega polja

Kaj je pretok električnega polja?

On pretok električnega polja ali preprosto električni pretok je skalarna količina, sorazmerna s številom električnih poljskih linij, ki prečkajo površino. Označuje ga kapitalski kapital φ (PHI).

Električno polje v resnici ne "teče" tako, kot to počne tok vode, čeprav pretočne črte tekočine spominjajo.

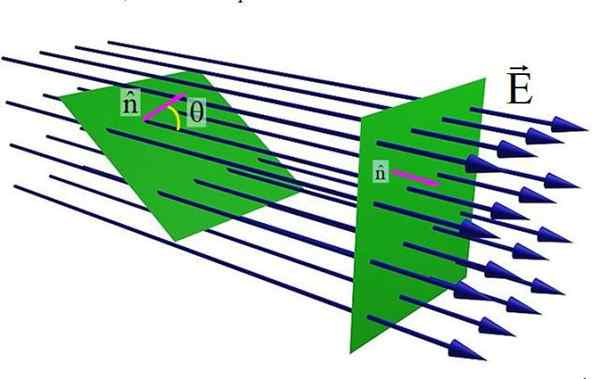
Slika 1. Električni poljski tok skozi ravno površino. Vir: Wikimedia Commons.

Zgornja slika prikazuje ravno površino, ki jo prečka električno polje In. Ko je običajni enotni vektor na površino n in polje In So vzporedne, količina poljskih črt, ki prečka površino, je največja. Ko pa se kot θ poveča med n in In, Število črt, ki se prenašajo skozi zeleno površino, je nižje.

Po drugi strani je pretok električnega polja odvisen tudi od obsega In, Ker je višje to, več poljskih linij prečkajo površino. In seveda, večje je območje S omenjene površine, tudi tok, zato je vzpostavljena naslednja enačba:

Φ = E ∙ SOSθ

Ta izraz je skladen s skalarnim izdelkom med vektorji In in n:

Φ = (In • n) S

Enota za pretok električnega polja v mednarodnem sistemu enot, če je n.m²/C (Newton X Square Metro/Coulomb). Ker se polje meri tudi v v/m (volt v podzemni železnici), je električni pretok v (v ∙ m) m).

Primeri

Po definiciji je električni tok lahko pozitiven, negativen ali enak 0. Pretok električnega polja je:

Lahko vam služi: magnetizacija: orbitalni in vrteni magnetni trenutek, primeri

-Pozitivno, ko je kot θ med In in n Je manj kot 90 °, saj je cos θ večji od nič.

-Negativno, če je ta kot večji od 90 °, ker je cos θ manjši od nič.

-Praznina, ko je θ vreden točno 90 °, ker COS 90 ° = 0 in poljske črte v tem primeru so tangencialne na površino.

-Na drugi strani, če je kot med In in n Je enak 0, tok pridobi svojo največjo vrednost.

Te možnosti so prikazane na naslednji sliki:

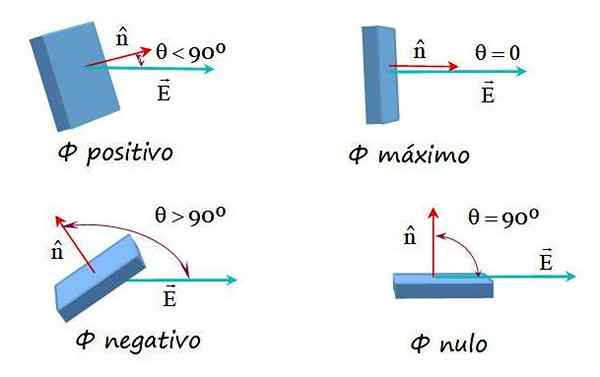Slika 2. Primeri pretoka električnega polja z različnimi usmeritvami med poljem in običajnim površinskim vektorjem. Vir: f. Zapata.

Pretok električnega polja na poljubni površini

Prej je bil pretok električnega polja določen v posebnem primeru enakomernega polja, ki vpliva na ravno površino. Za poljubno površino in/ali neenakomerno električno polje je kot med In in n se lahko razlikuje od točke do točke.

Na naslednji sliki sta dva primera, na levi ukrivljeni površini in na desni zaprti površini.

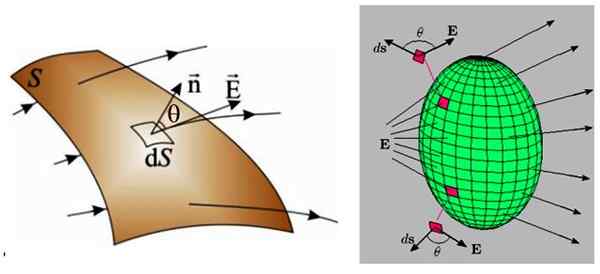Slika 3. Na levi strani poljubno površino, skozi katero se prečka neenakomerno električno polje. Na desni desno neenakomerno električno polje prečka zaprto površino, zato je neto tok v tem primeru ničen. Vir: f. Zapata.

V obeh primerih je površina razdeljena na veliko manjše regije neskončno majhne velikosti, imenovane DS, za katere prečka tudi neskončnomalni tok dφ:

dφ = (In•n) Ds = (ekosθ) ds

Skupno polje dobimo z dodajanjem vseh teh neskončno majhnih prispevkov:

Simbol S kot podpisovanja v integralu kaže, da ga je treba izračunati na celotni površini. Če je to zaprto, je označen z majhnim krogom na integralu:

Lahko vam služi: Antoine Constants: Formule, enačbe, primeri

V primeru zaprtih površin, n Vedno poudarite, tako da ima tok znak +, ko je odhajajoč, saj je kot med In in n je manjši od 90 ° in podpiše - ko je polje dohodno, ker potem kot med In in n je večji od 90 ° (glej sliko 2).

Upoštevajte, da je na zaprti površini na desni število poljskih linij, ki vstopijo na površino. Zato je neto tok, opredeljen kot algebrska vsota dohodnega toka in odhodni tok, praznina.

Vir električnega polja v tem primeru je zunaj površine, vendar bi bil neto pretok drugačen od 0, če bi bil vir električnega polja (porazdelitev obremenitev) znotraj površine.

Vaje

Vaja 1

Imate električno polje In = 3.5 kN/c x in ravno pravokotno površino 0.35 m široko za 0.7 m dolg. Poiščite tok električnega polja, ki v naslednjih primerih prečka pravokotnik:

a) Površina je vzporedna z ravnino yz.

b) Pravokotnik je vzporeden z ravnino xy.

c) Običajna ravnina tvori kot 40 ° z osi x in vsebuje os in.

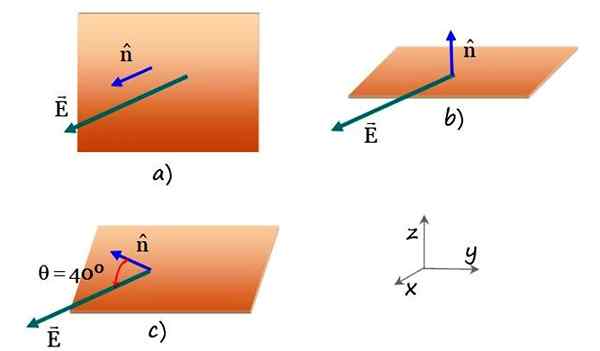Slika 4. Pravokotna ravnina, ki jo prečka enakomerno električno polje v različnih ravninskih usmeritvah. Vir: f. Zapata.

Rešitev

Običajni vektor in vektor električnega polja sta vzporedna, zato je kot θ med obema 0 ° in električni tok je:

Φ = (e ∙ s) cos 0 = e ∙ s

S površino pravokotnika je:

Vam lahko služi: Paralelogram metoda: primeri, rešene vaje

S = 0.35 m x 0.7 m = 0.245 m²

Zamenjava v φ:

Φ = e ∙ s = 3.5 x 10³ N/C × 0.245 m² = 857.5 n ∙ m² /C.

Rešitev b

Pretok električnega polja je 0, saj vektorji In in n Med seboj so pravokotni.

Rešitev c

Kot θ med poljem In in običajni vektor n je 40 ° (glej sliko), torej:

Φ = e ∙ s ∙ cos θ = 3.5 x 10³ N/C × 0.245 m² × cos 40 ° = 656.9 n ∙ m² /C.

Vaja 2

Izračunajte pretok električnega polja, ki proizvaja pozitivno točno obremenitev_tudi = 2 μC, ki se nahaja na sredini polmera sfere r = 5 cm.

Rešitev

Polje, ki ga je ustvarila obremenitev q_tudi Ni enotna, toda iz zakona Coulomb je znano, da ima na površini krogle veliko:

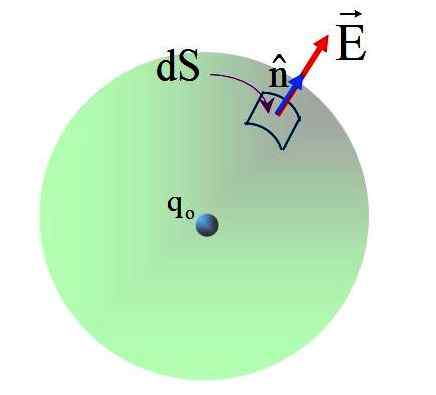Slika 5. Muhe polja, ki se na površini krogle proizvaja s točno obremenitvijo v središču. Vir: f. Zapata.

Polje ima radialno smer in običajni vektor n, Zato je kot med obema vektorji 0 na vseh točki sferične površine. Zamenjava:

Moraš:

DS -jev integral na celotni sferični površini je območje, ki je 4πr^2, Zato:

Ki zaključuje, da pretok električnega polja ni odvisen od površine S, ampak od obremenitve, zaklenjene v njej.

Njegova vrednost je:

Φ = 4π × 9 × 10⁹ x 2 × 10^-6 N⋅m²/C = 2.3 x 10⁵ N⋅m²/C

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Figueroa, d. (2005). Serija: Fizika za znanost in inženiring. Zvezek 5. Elektrostatika. Uredil Douglas Figueroa (USB).
3. Giambattista, a. 2010. Fizika. 2. mesto. Ed. McGraw Hill.
4. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.