Faktor stisljivosti, kako izračunati, primere in vaje

On Faktor stisljivosti z, o Kompresijski faktor za pline je brezdimenzionalna vrednost (brez enot), ki je uvedena kot popravek v enačbi stanja idealnih plinov. Na ta način matematični model bolj spominja na opaženo vedenje plina.

V idealnem plinu je enačba stanja, ki se nanaša na spremenljivke P (tlak), V (prostornina) in T (temperatura): Str.V _idealno = n.R.T z n = število molov in r = konstanta idealnih plinov. Če dodamo korekcijo faktorja stiskanja z, se ta enačba spremeni v:

Str.V = z.n.R.T

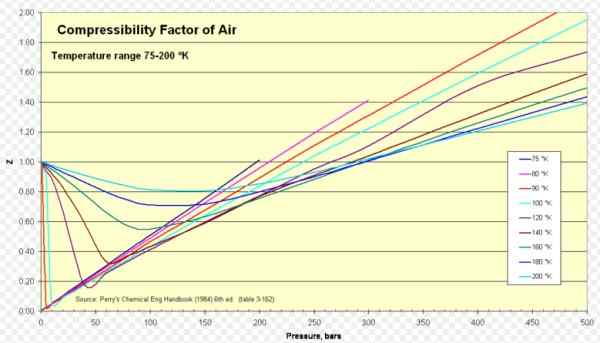
Slika 1. Faktor stisljivosti zraka. Vir: Wikimedia Commons. https: // nalaganje.Wikimedia.org/wikipedia/commons/8/84/compressional_factor_of_air_75-200_k.PNG.

[TOC]

Kako izračunati faktor stisljivosti?

Ob upoštevanju, da je molarni volumen V_kul = V/n, Imate pravi molarni volumen:

Str . V_Resnično = Z. R. T → Z = PV _Resnično/Rt

Ker je faktor stisljivosti z odvisen od pogojev plina, se izraža kot funkcija tlaka in temperature:

Z = z (p, t)

Če primerjamo prve dve enačbi, je ugotovljeno, da če je število molov n enako 1, je molarna prostornina resničnega plina povezana z novico idealnega plina do:

V_Resnično / V_idealno = Z → V _Resnično = Z v_idealno

Ko tlak presega 3 atmosfere, se večina plinov neha obnašati kot idealni plini in realna volumen se bistveno razlikuje od ideala.

To je v svojih poskusih uresničil nizozemski fizik Johannes van der Waals (1837-1923), zaradi česar je ustvaril model, ki se je bolje prilagodil praktičnim rezultatom kot enačba idealnih plinov: državna enačba van der Waals.

Vam lahko služi: natrijev oksalat (NA2C2O4): struktura, lastnosti, uporabe, tveganja

Primeri

Glede na enačbo Str.V_Resnično= Z.n.Rt, Za idealen plin, z = 1. Vendar pa v resničnih plinih s povečanjem pritiska tudi vrednost z. To je smiselno, ker imajo pri večjih tlačnih molekulah več možnosti za trčenje, zato se sile odbojnosti povečajo in s tem glasnost.

Po drugi strani se molekule premikajo z večjo svobodo in sile odbojnosti se zmanjšajo. Zato se pričakuje manjši volumen. Kar se tiče temperature, ko se poveča, se z zmanjša.

Kot je opazil van der Waals, je v bližini tako imenovane kritične točke plina zelo preusmerjeno iz idealnega plina.

Kritična točka (t_c, Str_c) katere koli snovi so vrednosti tlaka in temperature, ki določajo njihovo vedenje pred spreminjanjem faze:

-T_c To je temperatura, nad katero zadevni plin ni utekočinjen.

-Str_c  To je minimalni tlak, potreben za utekočinjenost plina pri temperaturi t_c

Vsak plin ima svojo kritično točko, ki določa temperaturo in znižan tlak t_r In p_r kot sledi:

Str_r = P / P_c

V_r = V /v_c

T_r = T /T_c

Opazimo, da je plin omejen z enakim V_r in T_r Izvedite enak pritisk Str_r. Zaradi tega, če je z grafično, odvisno od Str_r na isto T_r, Vsaka točka v tej krivulji je enaka za kateri koli plin. To se imenuje Načelo ustreznih držav.

Faktor stisljivosti v idealnih plinih, zraku, vodiku in vodi

Spodaj je krivulja stisljivosti za različne pline pri različnih znižanih temperaturah. Nato nekaj primerov Z za nekaj plinov in postopek za iskanje Z z uporabo krivulje.

Vam lahko služi: vodik: zgodovina, struktura, lastnosti in uporabe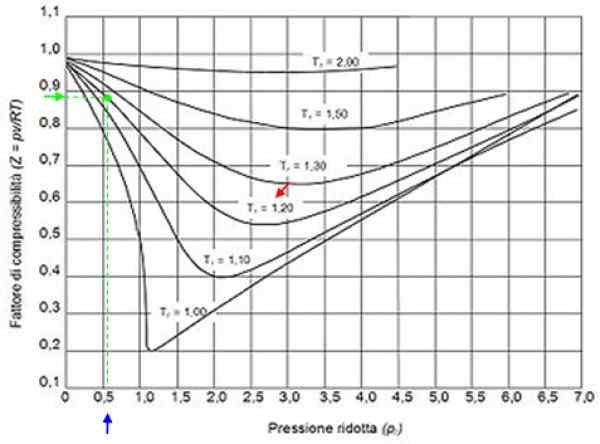Slika 2. Grafična faktorska grafika za pline v skladu z zmanjšanjem tlaka. Vir: Wikimedia Commons.

Idealni plini

Idealni plini imajo z = 1, kot je razloženo na začetku.

Zrak

Za zrak je z približno 1 v širokem razponu temperatur in pritiskov (glej sliko 1), kjer idealni model plina daje zelo dobre rezultate.

Vodik

Z> 1 za vse pritiske.

Voda

Za iskanje z vodo so potrebne vrednosti kritične točke. Kritična točka vode je: P_c = 22.09 MPA in T_c= 374.14 ° C (647.3 K). Ponovno je treba upoštevati, da je faktor stisljivosti z odvisen od temperature in tlaka.

Recimo, da želite najti z iz vode pri 500 ° C in 12 MPa. Potem je prva izračunati znižano temperaturo, za katero je treba Celzijeve stopnje prenesti na Kelvin: 50 ° C = 773 K:

T_r = 773/647.3 = 1.2

Str_r = 12/22.09 = 0.54

S temi vrednostmi najdemo v grafu slike krivulja, ki ustreza t_r = 1.2, označeno z rdečo puščico. Nato v vodoravni osi pogledamo vrednost p_r Bližje 0.54, označeno v modri barvi. Zdaj narišemo navpično, dokler ne prestrežemo t krivulje_r = 1.2 in končno je od te točke projiciran do navpične osi, kjer beremo približno vrednost z = 0.89.

Rešene vaje

Vaja 1

Obstaja vzorec plina pri temperaturi 350 K in tlak 12 atmosfer, pri čemer je molarni volumen 12 % višji od predvidenega zakona o idealnih plinih. Izračunati:

a) z kompresijski faktor.

b) molarna prostornina plina.

Vam lahko služi: nepopravljiva reakcija: značilnosti in primeri

c) Glede na zgornje rezultate navedite, katere so prevladujoče sile v tem vzorcu plina.

Podatki: r = 0,082 l.bankomat/mol.K

Rešitev

Vedeti, da je v _Resnično  je 12 % višji od V_idealno :

V_Resnično  = 1.12V_idealno

Z = v _Resnično / V_idealno = 1.12

Rešitev b

Str . V_Resnično = Z. R. T → V_Resnično = (1.12 x 0.082 x 350/12) l /mol = 2.14 l/mol.

Rešitev c

Sile odbojnosti so tiste, ki prevladujejo, saj se je volumen vzorca povečal.

Vaja 2

V prostornini 4 je 10 molov etana.86 L A 27 ° C. Poiščite pritisk, ki ga ima Ethan iz:

a) Idealen plin

b) enačba van der waals

c) Poiščite faktor stiskanja iz prejšnjih rezultatov.

Podatki za etana

Koeficienti Van Der Waals:

A = 5.489 dm⁶. Bankomat . mol^-2  in b = 0.06380 dm³. mol^-1.

Kritični tlak: 49 atm. Kritična temperatura: 305 K

Rešitev

Temperatura se prenese na Kelvin: 27 ° C = 27 +273 K = 300 K, tudi ne pozabite, da je 1 liter = 1 l = 1 dm³.

Nato se podatki, navedeni v idealni enačbi plina, nadomestijo:

Str.V = n.R.T → P = (10 x 0,082 x 300/4.86 l) atm = 50.6 atm

Rešitev b

Državna enačba Van der Waals je:

Kjer sta a in b koeficienta, ki jih daje izjava. Pri čiščenju P:

Rešitev c

Izračunamo znižani tlak in temperaturo:

Str_r = 35.2/49 = 0.72

T_r = 300 /305 = 0.98 ≈ 1

S temi vrednostmi se zahteva vrednost z v grafu slike 2 in ugotovi, da je z približno 0.7.

 Reference

1. Atkins, str. 1999. Fizikalna kemija. Omega izdaje.
2. Cengel in. 2012. Termodinamika. 7^ma Izdaja. McGraw Hill.
3. Engel, t. 2007. Uvod v fizikokemijo: termodinamika. Pearson.
4. Levine, i. 2014. Načela fizike-kemije. 6. Izdaja. McGraw Hill.
5. Wikipedija. Faktor stisljivosti. Pridobljeno iz: v.Wikipedija.org.