Skupne značilnosti faktorjev, primeri, vaje

On skupni dejavnik algebrskega izraza je znesek, ki je prisoten v vseh tokih. Ko je znan skupni faktor, je mogoče izraz na enakovreden način napisati skozi produkt dejavnikov.

Niso vsi algebrski izrazi skupni dejavnik, obstajajo samo tisti, ki jih je mogoče razdeliti le med njimi in 1, zato jih ni mogoče napisati kot produkt dejavnikov. Primer izražanja, ki nima skupnega dejavnika, je:

x + y

Slika 1. Skupni faktor algebrskega izraza je označen produkt dveh dejavnikov. Vir: Pixabay.

Namesto tega da:

5A + 10b

Vidi je, da je 5 prisoten v obeh pogledih, saj 10 = 5 ∙ 2. Ker je 5 skupni dejavnik, je mogoče zapisati naslednje:

5A + 10B = 5 ∙ (A + 2B)

Bralec lahko prek distribucijske lastnosti preveri, ali je izraz na desni enaki izvirniku.

Skupni faktor je lahko tudi dobeseden ali kombinacija števil in črk, na primer v 4x² - 2x. The x in 2 So med dejavniki in izraz ostaja kot izdelek:

4x² -2x = 2x⋅ (x - -1)

Prednost iskanja skupnega dejavnika izražanja in pisanja kot izdelka je, da je z njim skoraj vedno enostavno upravljati. Zato se uporablja v številnih algebrskih in izračunskih postopkih, kot so:

-Pri reševanju enačb, katerih rešitve se hitro razkrijejo, ko najdemo skupni faktor.

-Pri izračunu omejitve z nedoločnostjo lahko to izgine s pravilno faktorjem.

-Ustrezna faktorizacija olajša tudi operacije z racionalnimi algebrskimi izrazi, kot so vsote in odštevanja.

[TOC]

Skupne značilnosti faktorjev

Glavne značilnosti skupnega faktorja so naslednje:

-To je lahko številka, algebrski izraz ali kombinacija obeh.

-Skupni dejavnik mora biti v vsakem od izraza do faktorja.

Vam lahko služi: transcendentne funkcije: vrste, definicija, lastnosti, primeri

-Glede na količino izrazov, ki jih vsebuje, je to lahko:

1. Skupni monomni dejavnik, če je skupni dejavnik en sam izraz,
2. Pogost binomni faktor, če imate dva izraza in
3. Skupni polinomni faktor, če je skupni faktor sestavljen iz več izrazov.

Kako najti skupni faktor algebrskega izraza?

Če želite najti skupni faktor, ki je prisoten v polinomu, morate izračunati največji skupni delitelj ali MCD numeričnih koeficientov vseh izrazov, pa tudi črke ali literalce vsakega izraza in izbrati moč z najmanjšim eksponentom.

Črke ali dobesedne so lahko predstavljene kot monomi, binomi ali polinomi, kot je razvidno iz naslednjih primerov.

Najbolj priporočljivo razumeti postopek pridobivanja skupnega dejavnika, je slediti primeri in prakticiranje reševanja več vaj v vsakem primeru.

Skupni faktorski primeri

Ne smemo izgubiti razgleda dejstva, da je cilj skupnega faktorja pretvorjen izraz v naveden produkt dejavnikov. Potem se analizirajo najpomembnejši primeri:

Pogost monomialni dejavnik

Imate naslednje monomele (enomestni algebrski izrazi):

2x²; 10x⁴in; 100X⁶in²

Kaj je lahko skupni dejavnik za tri?

Začenši s številčnimi koeficienti: 2, 10 in 100, vsi so enakomerni in njihov MCD je 2. Kar zadeva dobesedni del, je spremenljivka X prisotna v treh izrazih, najnižja moč pa je x², Potem je skupni dejavnik 2x².

Trije predlagani pogoji lahko na ta način zapišemo kot izdelke tega dejavnika:

2x²= 2x²∙ 1

10x⁴y = 2x² ∙ 5x²in

100X⁶in²= 2x²∙ 50x⁴in²

Pomnoževanje dejavnikov na desni strani je mogoče preveriti, ali je izraz leve.

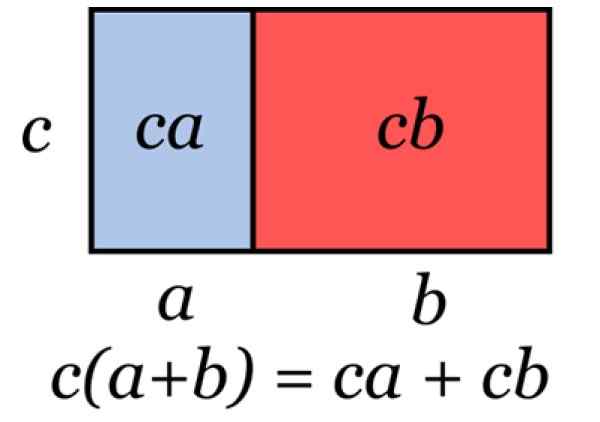Slika 2. Ilustracija, ki predstavlja skupni dejavnik. Vir: Wikimedia Commons.

Ta tehnika se uporablja, kadar je potrebna za upoštevanje algebrskega izraza, kot v naslednjih primerih:

• Primer 1

Dejstvo naslednji izraz:

Lahko vam služi: isosceles trikotnik

5x³in + 10x²in² + 5xy²

MCD numeričnih koeficientov vsakega izraza je:

Mcd (5.10) = 5

Kar zadeva dobesedni del, oba x kot in Prisotni so v treh izrazih in najmanj vsakega eksponenta je 1, zato je skupni dejavnik 5xy In lahko pišete:

5x³in + 10x²in² + 5xy²= 5xy ∙ (x² +2xy²+in)

Pogost polinomni faktor

Skupni dejavnik je lahko sestavljen iz binoma, trinomialnega ali na splošno v polinomu. V tem primeru so navodila v prejšnjem razdelku še vedno veljavna, saj kot skupni dejavnik izberejo tisti z najmanjšim eksponentom.

• Primer 2

Naslednji izraz napišite kot produkt dveh dejavnikov:

2A (x - 1) - 3B (x - -1)

Z neposrednim pregledom je skupni dejavnik binom (X-1), tako:

2a (x - 1) - 3b (x - 1) = (x -1) ∙ (2a - 3b)

Faktorizacija z razvrščanjem pogojev

Včasih obstoj skupnega dejavnika ni razviden, vendar se razkrije, če so izrazi razvrščeni na primeren način:

• Primer 3

Faktorizirajte 3x³ - 9AX² - x + 3a

Na prvi pogled v teh štirih izrazih ni skupnega dejavnika, saj na primer x Prisotna je v prvih treh, vendar ne v zadnjem. In do Je v drugem in v zadnjem ni nič več.

Kar zadeva koeficiente, obstajajo trije izrazi, v katerih je 3 prisoten, vendar je skupni dejavnik, bi moral biti v vseh pogojih.

Zdi se, da opisanih tehnik tokrat ni mogoče uporabiti. Vendar je izraz lahko upoštevan z razvrščanjem prvih dveh izrazov in zadnjih dveh, pri čemer je previden pri postavitvi oklepaja, da so znaki primerni, da ne spremenijo izvirnika:

Vam lahko služi: pravokotne sestavine vektorja (z vajami)

3x³ - 9AX² - x + 3a = (3x³ - 9AX²) - (x - 3a)

Upoštevajte negativni znak sredi oklepajev: potrebno je, ker bi se v nasprotnem primeru prvotni izraz spremenil.

V levi oklepaji je skupni dejavnik 3x², Zato:

(3x³ - 9AX²) - (x - 3a) = 3x²⋅ (x - 3a) - (x - 3a)

In opazimo, da se je že pojavil skupni dejavnik: (x - 3a), Se pravi, da je dejavnik že drugič, da dobite:

3x² (x- 3a) - (x - 3a) = (x - 3a) ∙ ( 3x²- 1)

Pogoste faktorske vaje

Vaja 1

Rešite 4x enačbo³ +7x²  +6x = 0

Rešitev

"X" je torej pogost dejavnik:

3x³ −5x²  +2x = x (3x² −5x +2) = 0

Za izraz levo je 0, dovolj je, da je izpolnjen eden od teh dveh pogojev:

x = 0

Eno:

3x² −5x +2 = 0

To je popolna enačba druge stopnje, ki jo je mogoče rešiti z uporabo splošne formule, tudi z uporabo znanstvenega kalkulatorja ali druge algebrske metode. Rešitve te enačbe so:

x = 1

x = 2/3

Ko ga najdemo, je ponazoritev pisati enačbo kot produkt treh dejavnikov, čeprav izjava tega ni zahtevala. Bilo bi tako:

x⋅ (x-1) ⋅ (x-2/3) = 0

Vaja 2

Izračunajte naslednjo mejo, če obstaja:

Rešitev

Najprej ga zamenjamo pri x = −2, da poskusi oceniti mejo, pri tem pa dobimo:

Ker gre za nedoločnost obrazca 0/0, morate biti dejavnik, da ga poskušate odpraviti. Imenovalec ne more biti dejavnik, vendar števca to počne.

V štetju je skupni dejavnik x:

x²+2x = x ∙ (x+2)

Faktorizirani izraz se nadomesti v meji in na ta način nedoločnost izgine:

Ugotovljeno je, da meja obstaja in je vredna −2.

Reference

1. Baldor, a. 2005. Algebra. Kulturna domovinska skupina.
2. Jiménez, r. 2008. Algebra. Dvorana Prentice.
3. Larson, r. 2012. Prekalenkulacija. 8. Izdaja. Cengage učenje.
4. Stewart, J. 2007. Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
5. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.