Ali obstajajo skalni trikotniki s pravim kotom?

Obstaja veliko scalile trikotnikov z pravim kotom. Preden napredujemo na to temo, je treba najprej vedeti različne vrste trikotnikov, ki obstajajo. Trikotnike sta razvrščena po dveh razredih, ki sta: njihovi notranji koti in dolžine njihovih strani.

Vsota notranjih kotov katerega koli trikotnika je vedno enaka 180 °. Toda v skladu z notranjimi koti so ukrepi razvrščeni kot:

-Akutant: Ti trikotniki so takšni, da so njihovi trije koti akutni, to je, da merijo manj kot 90 °.

-Pravokotnik: To so tisti trikotniki, ki imajo pravi kot, to je kot, ki meri 90 °, zato sta druga dva kota akutna.

-Obtuse: To so trikotniki, ki imajo prikrit kot, to je kot, katerega ukrep je večji od 90 °.

Trikotniki Scalan z desnim kotom

Zanimanje za ta del je ugotoviti, ali ima lahko trikotnik skale pravi kot.

Kot rečeno zgoraj, je pravi kot kot 90 ° 90 °. Poznati je treba le definicijo skalenskega trikotnika, ki je odvisna od dolžine strani trikotnika.

Razvrstitev trikotnikov glede na njihove strani

Glede na dolžino svojih strani so trikotniki razvrščeni kot:

-Enakostranično: Vsi ti trikotniki so tako, da so dolžine njihovih treh strani enake.

-Izosceles: To so trikotniki, ki imajo natanko dve strani enake dolžine.

-Scalene: To so tisti trikotniki, na katerih imajo tri strani različne ukrepe.

Formulacija enakovrednega vprašanja

Vprašanje, ki je enakovredno vprašanju naslova, je: "Ali obstajajo trikotniki, ki imajo vse tri strani z različnimi ukrepi in to ima kot 90 °?"

Odgovor, kot je navedeno na začetku, je pritrdilen. Tega odgovora ni zelo težko utemeljiti.

Če ga natančno opazimo, noben pravokotnik trikotnik ni enakostraničen, to je mogoče upravičiti zahvaljujoč teoremu pitagore za pravokotne trikotnike, ki pravi:

Glede na pravokotnik trikotnika, da sta dolžina njihovih kategorij "a" in "b", dolžina njegove hipotenuse pa je "c", morate c² = a²+b², kar je razvidno, da dolžina hipotenuze " C "je vedno večji od dolžine vsake noge.

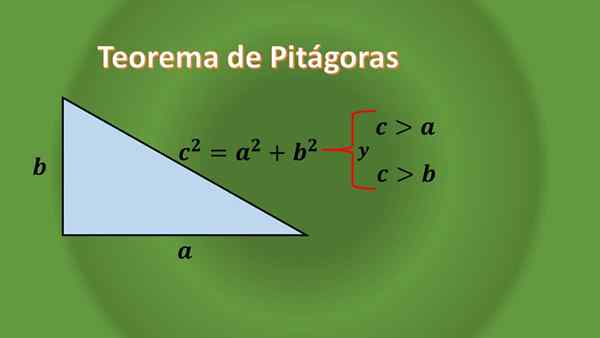
Ker se o "A" in "B" nič ne reče, potem to pomeni, da je pravi trikotnik lahko izoscele ali Scalene.

Nato samo izberite kateri koli pravokotnik Trikotnik, tako da imajo njegove noge različne ukrepe, in s tem izbran teodrični trikotnik, ki ima pravi kot.

Primeri

-Če upoštevamo pravokotnik trikotnik, katerih noge imajo dolžine 3 oziroma 4. To pomeni, da je trikotnik Scalene in ima pravi kot.

-Naj bo ABC pravokotnik trikotnik z meritvami 1 in 2. Potem je dolžina njegove hipotenuze √5, kar sklepa, da je ABC trikotnik Scalene pravokotnik.

Ni vsak trikotnik v lestvici pravega kota. Lahko upoštevate trikotnik, kot je na naslednji sliki, ki je Scalene, vendar noben njegov notranji zorni koti ni raven.

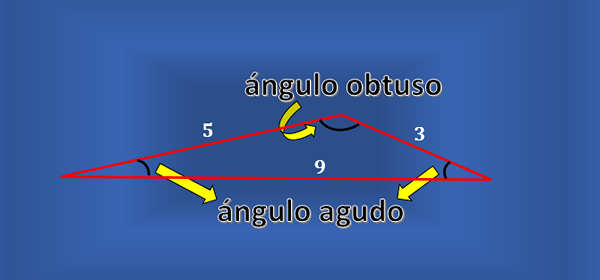Poleg tega ni vsak pravi trikotnik Scalene. Če upoštevate pravi trikotnik, katerega noge merijo oboje 1, bo hipotenuza imela merilo √2. Zato je pravokotnik trikotnik izoscele.