Vektorski prostor za osnovno in dimenzijo, aksiomi, lastnosti

A vektorski prostor Je nepranski komplet V= ali, v, W,…, katerih elementi so vektorji. Z njimi se izvaja nekaj pomembnih operacij, med katerimi izstopajo naslednje:

- Vsota med dvema vektorjem u + v kot rezultat z, ki spada v celoto V.

- Množenje realnega števila α z vektorjem v: α v ki daje še enega vektorja in ki pripada V.

Umetniška vizija vektorskega prostora. Vir: Pixabay

Za označevanje vektorja uporabljamo krepko (v Je vektor) in za skalarje ali številke grške črke (α je številka).

[TOC]

Aksiomi in lastnosti

Če želite biti vektorski prostor, je treba izpolniti naslednjih osem aksiomov:

1-konmutabilnost: ali +v = v +ali

2-tranzibility: (ali + v) + W = ali + ( v + W)

3-obstoji ničelnega vektorja 0 takšno, da 0 + v = v

4-obstoječa: nasprotno od v je (-v) , glede na to v + (-v) = 0

5-proizvodna distribucija glede na vektorsko vsoto: α ( ali + v ) = αali +αv

6-proizvodna distribucija glede na skalarno vsoto: (α + β)v = αv +βv

7-asociativnost skalarnega izdelka: α (β v) = (α β)v

8-številka 1 To je nevtralen element od takrat: 1v = v

Primeri vektorskih prostorov

Primer 1

Vektorji v ravnini (R²) so primer vektorskega prostora. Vektor v ravnini je geometrijski predmet, ki ima velikost in smer. Predstavljen je z orientiranim segmentom, ki spada v omenjeno ravnino in z velikostjo sorazmerne z njegovo velikostjo.

Vsota dveh vektorjev v ravnini lahko definiramo kot geometrijsko delovanje drugega vektorja po prvem. Rezultat vsote je usmerjen segment, ki se začne od izvora prvega in doseže konico drugega.

Na sliki je mogoče ugotoviti, da je vsota v R² komutativna.

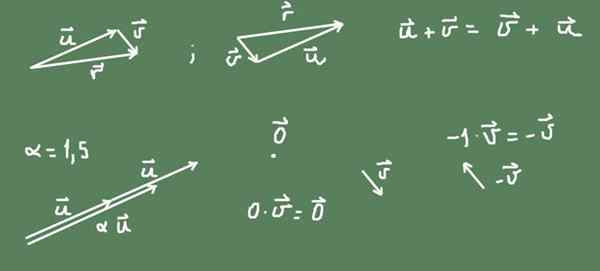Slika 2. Vektorji v ravnini oblikujejo vektorski prostor. Vir: Self Made.

Izdelek α številke je opredeljen tudi z vektorjem. Če je številka pozitivna, se vzdržuje originalni vektorski naslov in velikost je α krat večja od prvotnega vektorja. Če je številka negativna, je naslov nasproten in nastala velikost vektorske velikosti je absolutna vrednost številke.

Vektor, ki nasprotuje vektorju v je -v = (-1) v.

Null Vector je točka v ravnini R², ničelna številka pa z vektorjem povzroči ničelni vektor.

Vse rečeno je prikazano na sliki 2.

Primer 2

Set Str Od vseh polinomov, manjših ali enakih dveh, vključno z ničelno stopnjo, tvorijo komplet, ki ustreza vsem aksiomom vektorskega prostora.

Lahko vam služi: medsebojno izključujoči dogodki: lastnosti in primeri

Biti polinom p (x) = a x² + b x + c y q (x) = d x² + e x + f

Vsota dveh polinomov je definirana: p (x) + q (x) = (a + d) x² + (b + e) ​​x + (c + f)

Vsota polinomov, ki pripadajo celoti Str Je komutativna in prehodna.

Ničelni polinom, ki pripada celoti Str To je tisti, ki ima vse svoje koeficiente, enake ničle:

0 (x) = 0 x² + 0 x + 0

Vsota α skalar je opredeljena s polinomom, kot je: α p (x) = α ∙ a x² + α ∙ b x + α ∙ c

Nasprotni polinom p (x) je -p (x) = (-1) p (x).

Iz vsega zgoraj navedenega izhaja, da je nabor Str Od vseh polinomov, manjših ali enakih dveh, je vektorski prostor.

Primer 3

Set M Od vseh matric m vrstic x n stolpcev, katerih elementi so realne številke, tvorijo resnični vektorski prostor glede na vsoto matric in produkta števila z matrico.

Primer 4

Nabor F neprekinjenih funkcij resnične spremenljivke, tvori vektorski prostor, saj je mogoče definirati vsoto dveh funkcij, množenje skalar s funkcijo, ničelno funkcijo in simetrično funkcijo. Izpolnjujejo tudi aksiome, ki so značilni za vektorski prostor.

Baza in dimenzija vektorskega prostora

Baza

Nabor linearno neodvisnih vektorjev je opredeljen kot osnova vektorskega prostora, tako da iz linearne kombinacije njih lahko ustvarite kateri koli vektor tega vektorskega prostora.

Linearno kombiniranje dveh ali več vektorjev je sestavljeno iz množenja vektorjev z nekaterimi skalarnimi in jih nato vektorsko dodajanje.

Na primer, v vektorskem prostoru vektorja v treh dimenzijah, ki jih tvori R³, se uporablja kanonična baza, ki jo definirajo enotni vektorji (z magnitudo 1) (z magnitudo 1) Yo, J, k.

Kje Yo = (1, 0, 0); J = (0, 1, 0); k = (0, 0, 1). To so kartezijanski ali kanonični vektorji.

Kateri koli vektor V pripada r³ napisana kot V = a Yo + b J + c k, ki je linearna kombinacija osnovnih vektorjev Yo, J, k. Scalars ali številke A, B, C so znane kot kartezijanske komponente V.

Govori se tudi, da osnovni vektorji vektorskega prostora tvorijo niz vektorskega prostora.

Dimenzija

Dimenzija vektorskega prostora je kardinalna številka vektorske baze za omenjeni prostor; to pomeni število vektorjev, ki sestavljajo omenjeno bazo.

Ta kardinal je največje število linearno neodvisnih vektorjev tega vektorskega prostora, hkrati pa najmanjše število vektorjev, ki tvorijo nabor proizvodnje.

Vam lahko služi: statistična populacija: koncept, vrste, primeri

Osnove vektorskega prostora niso edinstvene, vendar imajo vse podlage istega vektorskega prostora enako dimenzijo.

Vektorski podprostor

Vektorski podprostor vektorskega prostora V je podskupina V, v kateri so enake operacije opredeljene kot v V in izpolnjuje vse aksiome vektorskega prostora. Zato bo podprostor tudi vektorski prostor.

Primer vektorskega podprostora so vektorji, ki pripadajo ravnini XY. Ta podprostor je podskupina vektorskega prostora dimenzij, večjega od nabora vektorjev, ki pripadajo trijedimenzionalnemu prostoru XYZ.

Drug primer vektorskega podprostora S1 vektorskega prostora tvori vse 2 × 2 matrike z resničnimi elementi, ki je opredeljen spodaj:

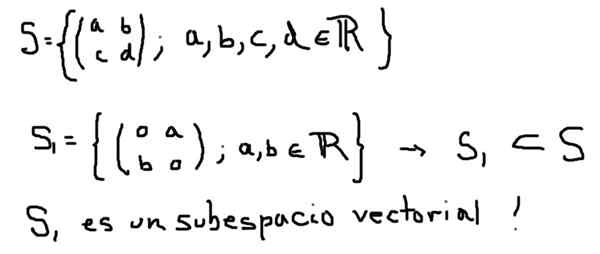
Po drugi strani pa je S2 opredeljen spodaj, čeprav gre za podmnožico S, ne tvori vektorskega podprostora:

Rešene vaje

-Vaja 1

Biti vektorji V1= (1, 1, 0); V2= (0, 2, 1) in V3= (0, 0, 3) v r³.

a) Dokažite, da so linearno neodvisne.

b) Dokažite, da tvorijo osnovo v R³, saj lahko kateri koli seznam (x, y, z) zapišemo kot linearno kombinacijo v1, v2, v3.

c) Poiščite komponente seznama V = (-3,5,4) na dnu V1, V2, V3.

Rešitev

Kriterij za prikaz linearne neodvisnosti je določiti naslednji niz enačb v α, β in γ

α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3) = (0, 0, 0)

V primeru, da je edina rešitev tega sistema α = β = γ = 0, potem so vektorji linearno neodvisni, sicer niso.

Za dosego vrednosti α, β in γ predlagamo naslednji sistem enačb:

α ∙ 1 + β ∙ 0 + γ ∙ 0 = 0

α ∙ 1 + β ∙ 2 + γ ∙ 0 = 0

α ∙ 0 + β ∙ 1 + γ ∙ 3 = 0

Prva vodi do α = 0, drugega α = -2 ∙ β, vendar kot α = 0, potem β = 0. Tretja enačba pomeni, da je γ = (-1/3) β, vendar kot β = 0, potem γ = 0.

Odgovor na

Ugotovljeno je, da gre za niz linearno neodvisnih vektorjev v R³ .

Odgovor b

Zdaj pa napišite seznam (x, y, z) kot linearno kombinacijo v1, v2, v3.

(x, y, z) = α v1 + β v2 + γ v3 = α (1, 1, 0) + β (0, 2, 1) + γ (0, 0, 3)

α ∙ 1 + β ∙ 0 + γ ∙ 0 = x

α ∙ 1 + β ∙ 2 + γ ∙ 0 = y

Lahko vam služi: Tukey Test: Kaj je v primeru, da je v primeru rešena vaja

α ∙ 0 + β ∙ 1 + γ ∙ 3 = z

Kjer imate:

α = x

α + 2 β = y

β + 3 γ = z

Prva označuje α = x, drugi β = (y-x)/2 in tretji γ = (z-y/2 +x/2)/3. Na ta način smo našli generatorje α, β in γ katerega koli seznama R³ 

Odgovor c

Poiščite komponente seznama V = (-3,5,4) na dnu V1, V2, V3.

Zamenjamo ustrezne vrednosti v zgoraj najdenih izrazih za generatorje.

V tem primeru imamo: α = -3; β = (5-(-3))/2 = 4; γ = (4- 5/2 +(- 3)/2)/3 = 0

To je:

(-3,5,4) = -3 (1, 1, 0) + 4 (0, 2, 1) + 0 (0, 0, 3)

Končno:

V = -3 V1 + 4 V2 + 0 V3

To sklepamo V1, v2, v3 Tvorijo bazo v vektorskem prostoru R³ dimenzije 3.

-Vaja 2

Express polinom p (t) = t² + 4t -3 kot linearna kombinacija p1 (t) = t² -2t + 5, p2 (t) = 2t² -3t in p3 (t) = t + 3.

Rešitev

P (t) = x p1 (t) + in p2 (t) + z p3 (t)

kjer je treba določiti številke x, y, z.

Z množenjem in razvrščanjem izrazov z isto stopnjo v t se dobi:

T² + 4 t -3 = (x + 2y) t² + (-2x -3y + z) t + (5x + 3z)

Kar nas vodi do naslednjega sistema enačb:

x + 2y = 1

-2x -3y + z = 4

5x + 3z = -3

Rešitve tega sistema enačb so:

x = -3, y = 2, z = 4.

To je:

P (t) = -3 p1 (t) + 2 p2 (t) + 4 p3 (t)

-Vaja 3

Pokažite, da vektorji V1= (1, 0, -1, 2); V2= (1, 1, 0, 1) in V3= (2, 1, -1, 1) R⁴ so linearno neodvisni.

Rešitev

Linearno kombiniramo tri vektorje V1, V2, V3 In zahtevamo, da kombinacija doda ničelni element r⁴

do V1 + b V2 + c V3 = 0

To pomeni,

A (1, 0, -1, 2) + B (1, 1, 0, 1) + C (2, 1, -1, 1) = (0, 0, 0, 0)

To nas vodi do naslednjega sistema enačb:

A + b + 2 c = 0

B + C = 0

-A - c = 0

2 a + b + c = 0

Odštejemo prvo in četrto, imamo: -a + c = 0 Kaj pomeni a = c.

Če pa pogledamo tretjo enačbo, moramo = -C. Edini način za izpolnitev a = c = (-c) je, da je C 0 in bo zato tudi 0.

A = c = 0

Če ta rezultat nadomestimo v prvi enačbi, potem sklepamo, da je B = 0.

Končno a = b = c = 0, zato je mogoče sklepati, da so vektorji V1, V2 in V3 linearno neodvisni.

Reference

1. Lipschutz, s. 1993. Linearna algebra. Druga izdaja. McGraw - Hill. 167 - 198.