Običajni napor, iz česa je sestavljen, kako je izračunano, primeri

On normalen napor Uporablja se pri določenem materialu, imenovanem tudi enoosni napori, to je povezava med uporabljeno silo, pravokotno na določeno površino, in območjem, na katerem deluje, ali obremenitvijo na enoto območja. Matematično, če je P velikost sile in je A območje, kjer se uporablja, je napor σ količnik: σ = p/a.

Enote običajnih naporov v mednarodnem sistemu so Newton /Metro², znan kot pascal in skrajšano PA. To so enake tlačne enote. Druge enote, ki se pojavljajo v literaturi, so pogosto kilogrami / palčni² tudi psi.

Slika 1. Kamni se nenehno podvržejo prizadevanjem zaradi tektonske aktivnosti, kar povzroča deformacije v Zemljini skorji. Vir: Pixabay.

Na sliki 2 se dve sili enake velikosti uporabljata pravokotno na območje prereza, pri čemer se vlečeta na zelo lahki palici, ki jo razširja.

Te sile prinašajo normalen napor, ki se imenuje tudi Aksialna obremenitev osredotočeno, ker njegova linija delovanja sovpada z osjo osi, na kateri se nahaja centroid.

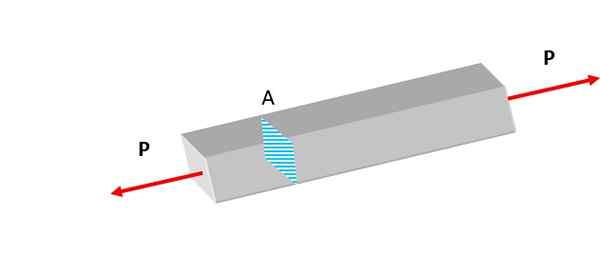Slika 2. Prikazana vrstica je podvržena vlečnim silam. Vir: Self Made.

Prizadevanja, ne glede na to, ali so običajni ali drugi tipi, se nenehno pojavljajo v naravi. V litosferi so kamnine podvržene gravitaciji in tektonski aktivnosti, ki eksperimentirajo deformacije.

Na ta način izvirajo strukture, kot so gube in okvare, katerih študija je pomembna pri uporabi mineralov in gradbeništva, za gradnjo stavb in cest, če naštejem nekaj primerov.

[TOC]

Kako se izračuna?

Enačba, podana na začetku σ = P/A, omogoča izračun povprečnega normalnega napora na zadevnem območju. Vrednost P je velikost nastale sile na območju, ki se nanaša na centroid, in zadostuje za številne preproste situacije.

V tem primeru je porazdelitev sil enakomerna, še posebej na točkah, oddaljenih od mesta, kjer imate vrstico, ki je podvržena vleki ali stiskanju. Če pa je potreben napor za izračun na določeni točki ali sile niso enakomerno razporejene, je treba uporabiti naslednjo definicijo:

Vam lahko služi: zaprto električno vezje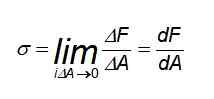

Potem se na splošno lahko vrednost truda na določeni točki razlikuje od povprečne vrednosti. Pravzaprav se lahko trud razlikuje v skladu z oddelkom, ki ga je treba upoštevati.

To je prikazano na naslednji sliki, v kateri vlečne sile poskušajo ločiti palico v ravnovesju v razdelkih mm in nn.

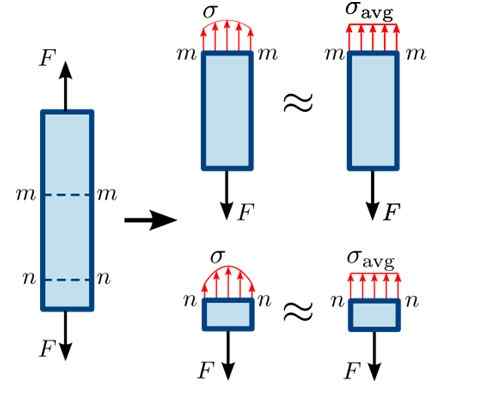Slika 3. Porazdelitev normalnih prizadevanj v različnih odsekih bara. Vir: https: // commons.Wikimedia.org/wiki/datoteka: običajna_Stress.SVG#/Media/File: Normal_Stress.SVG

Kot odsek nn Je zelo blizu, kjer je sila F navzdol, porazdelitev sil na površini ni povsem homogena, ti mladoletniki so dlje od tega trenutka. Porazdelitev je v razdelku nekoliko bolj homogena mm.

V vsakem primeru se normalni napor vedno nagiba k raztezanju ali stisnju obeh delov telesa, ki jih najdemo na obeh straneh ravnine, na katerih delujejo. Po drugi strani se druga različna prizadevanja, kot je striženje, ponavadi premikajo in ločujejo te dele.

Hookejev zakon in normalen napor

Hookejev zakon navaja, da je v mejah elastike normalno prizadevanje neposredno sorazmerno z deformacijo, ki jo doživlja palica ali predmet. V tem primeru:

Normalen napor ∝ Enotna deformacija

Konstanta sorazmernosti je mladi (y) modul:

Običajni napor (σ) = mladi modul (y) x enotna deformacija (ε)

σ = y. ε

Z ε = ΔL/L, kjer je ΔL razlika med končno in začetno dolžino, ki je l.

Mladi modul ali modul elastičnosti je značilen za material, katerega dimenzije so enake kot pri trudu, saj je deformacija enote brez dimenzije.

Lahko vam služi: 13 primerov Newtonovega drugega zakona v vsakdanjem življenju

Pomen truda pri odpornosti materialov in geologije

Določitev, kako odporni so materiali na prizadevanja, je zelo pomembno. Za konstrukcije, ki se uporabljajo pri gradnji stavb, pa tudi pri oblikovanju delov za različne naprave, je treba zagotoviti, da izbrani materiali pravilno izpolnjujejo svojo funkcijo.

Zato se materiali izčrpno analizirajo v laboratorijih s preskušanji, namenjenimi vedeti, koliko sile se lahko upirajo, preden se deformirajo in lomijo, s čimer izgubijo svoje funkcije. Na podlagi tega je sprejeta odločitev o tem, ali bomo izdelali določen kos ali pa del naprave.

Verjame se, da je bil prvi znanstvenik, ki je sistematično preučil odpor gradiva Leonardo da Vinci. Pustil je dokaze o preskušanjih, v katerih je določil odpor žic, ki visijo kamne različnih pesosov.

V prizadevanjih sta pomembna tako razsežnost sile kot tudi dimenzije strukture in kako se uporablja, da se določi meje, znotraj katerih ima material elastično vedenje; to pomeni, da se vrne v prvotno obliko, ko trud preneha.

Z rezultati teh testov se za različne vrste materialov, kot so jeklo, beton, aluminij in še veliko več.

Primeri

V naslednjih primerih se domneva, da so sile enakomerno razporejene in da je material homogeno in izotropno. To pomeni, da so njegove lastnosti enake v kateri koli smeri. Zato je veljavno uporabiti enačbo σ = p/a za iskanje prizadevanj.

-Vaja 1

Na sliki 3 je znano, da ima povprečni normalni napor, ki deluje na odsek AB, magnitudo 48 kPa. Poiščite: a) Obseg sile F, ki deluje v CB, b) napor na oddelku BC.

Lahko vam služi: horizontalno streljanje: značilnosti, formule in enačbe, vaje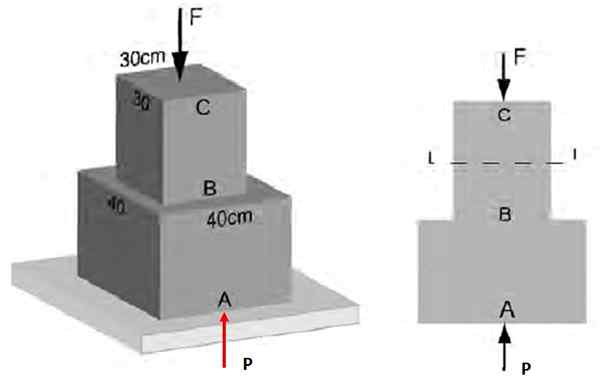Slika 4. Običajna prizadevanja na strukturi primera 1 ..

Rešitev

Ker je struktura v statičnem ravnovesju, po Newtonovem drugem zakonu:

P-f = 0

Običajni napor na oddelku AB ima velikost:

σ_Ab = P/A_Ab

Kjer je p = σ_Ab . Do_Ab = 48000 PA. (40 x 10 ^-2 m)² = 7680 n

Zato f = 7680 n

Običajni napor na odseku BC je razmerje med velikostjo F in površino preseka na tej strani:

σ_Pr = F/a_Pr = 7680 N / (30 x 10 ^-2 m)² = 85.3 kPa.

-Vaja 2

150 m žice dolga in 2.Premera 5 mm je raztegnjena s silo 500 N. Najti:

a) vzdolžni napor σ.

b) enotna deformacija, vedoč, da je končna dolžina 150.125 m.

c) modul elastičnosti In te žice.

Rešitev

a) σ = f / a = f / π.r²

Polmer žice je polovica premera:

R = 1.25 mm = 1.25 x 10^-3 m.

Območje prereza je π.r², Potem je trud:

σ = f / π.r² = 500 / (π.(1.25 x 10^-3)² PA = 101859.2 Pa

b) ε = ΔL / l = (končna dolžina - začetna dolžina) / začetna dolžina

Zato:

ε = (150.125 - 150) /150 = 0.125/150 = 0.000833

c) Young -ov modul žice se očisti tako, da poznamo vrednosti ε in σ, ki so bile predhodno izračunane:

Y = σ / ε = 101859.2 Pa / 0.000833 = 1.22 x 10⁸ PA = 122 MPA.

Reference

1. Pivo, f. 2010. Mehanika materialov. 5. Izdaja. McGraw Hill. 7 - 9.
2. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6^tth  Ed. Dvorana Prentice. 238-242.
3. Hibbeler, R.C. 2006. Mehanika materialov. 6. Izdaja. Pearson Education. 22 -25
4. Valera Negrete, J. 2005. Splošne zapise o fiziki. Ne. 87-98.
5. Wikipedija. Stres (mehanika). Okreval od: Wikipedia.org.