Termično ravnotežno enačbe, aplikacije, vaje

Toplotno ravnovesje dveh teles, ki sta v toplotnem stiku, je stanje, ki ga dosežemo po dovolj dolgem času.

V termodinamiki se toplotni stik dveh teles (ali dveh termodinamičnih sistemov) razume kot situacija, v kateri imajo telesa mehanski stik ali so ločeni, vendar v stiku s površino, ki omogoča samo prehod toplote iz enega telesa (diathermična površina (diathermična površina ).

Slika 1. Čez nekaj časa bo led in pijača dosegla njihovo toplotno ravnovesje. Vir: Pixabay

Pri toplotnem stiku ne sme biti kemične reakcije med sistemi v stiku. Obstaja samo izmenjava toplote.

Vsakodnevne situacije, v katerih je izmenjava toplote, med mnogimi drugimi primeri predstavljajo sisteme, kot so hladna pijača in steklo, vroča kava in čajna žlička ali telo in termometer.

[TOC]

Ko sta dva ali več sistemov v toplotnem ravnovesju?

Drugi zakon termodinamike določa, da toplota vedno preide od najvišje temperaturne telesa do najnižje temperature. Prenos toplote preneha takoj, ko se temperature izenačijo in dosežemo status toplotnega ravnovesja.

Praktična uporaba toplotnega ravnovesja je termometer. Termometer je naprava, ki meri svojo temperaturo, toda zahvaljujoč toplotnemu ravnovesju lahko poznamo temperaturo drugih teles, na primer osebe ali živali.

Termometer stolpca Mercury je nameščen v toplotnem stiku s telesom, na primer pod jezikom, in pričakuje se, da bo dovolj časa dosegel toplotno ravnovesje med telesom in termometrom in da se njegovo odčita.

Ko je ta točka dosežena, je temperatura termometra enaka telesu.

Ničetni zakon termodinamike ugotovi, da če je telo A v toplotnem ravnovesju s telesom C in je isto telo C v toplotnem ravnovesju z B, potem sta A in B v toplotnem ravnovesju, tudi če med A in B ni toplotnega stika.

Zaključujemo, da sta dva ali več sistemov v toplotnem ravnovesju, kadar imata enako temperaturo.

Termične ravnotežne enačbe

Predvidevamo telo pri začetni temperaturi v toplotnem stiku z drugim telesom B z začetno temperaturo TB. Domnevamo tudi, da se ta> tb, potem po drugem zakonu toplota prenese iz A na B.

Čez nekaj časa bo doseženo toplotno ravnovesje in oba telesa bosta imela enako končno temperaturo TF. To bo imelo vmesno vrednost za TA in TB, torej ta> tf> tb.

Količina toplote, prenesene od A na B, bo QA = Ma Ca (TF - TA), kjer je MA masa telesa A, Ca Toplotna zmogljivost na enoto mase A Y (tf - TA) Temperaturna razlika. Če je TF manjši od potem je QA negativna, kar kaže, da telo daje toploto.

Podobno za telo B morate QB = MB CB (TF - TB); In če je TF večji od TB, je QB pozitiven, kar kaže, da telo B prejme toploto. Ker sta telo A in B v toplotnem stiku med njima, vendar izolirani iz okolja, mora biti skupna količina izmenjane toplote NULL: QA + QB = 0

Potem ma ca (tf - ta) + mb cb (tf - tb) = 0

Temperatura ravnotežja

Če razvijamo ta izraz in čiščenje temperature TF, dobimo končno temperaturo toplotnega ravnotežja.

Slika 2. Končna temperatura ravnotežja. Vir: Self Made

Tf = (ma ca ta + mb cb tb) / (ma ca + mb cb).

Kot poseben primer upoštevajte primer, da sta telesa A in B enaka pri masi in v toplotni zmogljivosti, v tem primeru bo ravnotežna temperatura:

Tf = (ta + tb) / 2 ↔, če je ma = mb in ca = cb.

Toplotni stik s fazno spremembo

V nekaterih situacijah se zgodi, da ko sta dva telesa postavljena v toplotni stik, izmenjava toplote povzroči spremembo stanja ali faze v enem od njih. Če se to zgodi, je treba upoštevati, da med fazno spremembo ni temperaturne spremembe telesa, ki spreminja njegovo stanje.

Če pride do fazne spremembe enega od teles v toplotnem stiku, se uporabi koncept latentne toplote L, ki je energija na enoto mase, potrebna za spremembo stanja:

Q = l ∙ m

Na primer, da se stopi 1 kg ledu pri 0 ° C, je potrebnih 333,5 kJ/kg in ta vrednost je latentna toplota taljenja ledu.

Med fuzijo se trdna voda spremeni v tekočo vodo, vendar voda med postopkom združitve ohranja isto temperaturo ledu.

Prijave

Toplotno ravnovesje je del vsakdanjega življenja. Na primer, podrobno preučimo to situacijo:

-Vaja 1

Oseba se želi kopati s toplo vodo pri 25 ° C. V kocki položite 3 litre hladne vode pri 15 ° C in v kuhinjski vročini do 95 ° C.

Koliko litrov vroče vode mora dodati kocki hladne vode, da ima želeno končno temperaturo?

Rešitev

Recimo, da je hladna voda in B vroča voda:

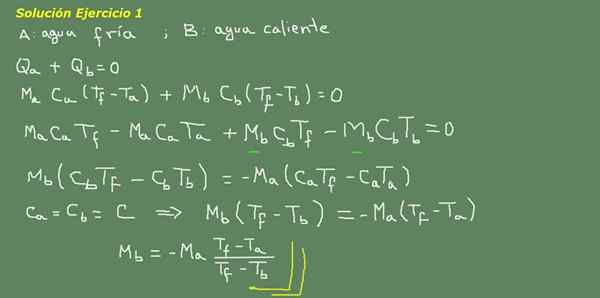Slika 3. Vaja 3 rešitev. Vir: Self Made.

Predlagamo enačbo toplotnega ravnotežja, kot je prikazano na plošči na sliki 3 in od tam očistimo MB vodo.

Začetna masa hladne vode je mogoče dobiti, ker je znana gostota vode, ki je 1kg za vsak liter. To pomeni, da imamo 3 kg hladne vode.

Ma = 3kg

Tako

MB = - 3 kg*(25 ° C - 15 ° C)/(25 ° C - 95 ° C) = 0,43 kg

Potem je dovolj z 0,43 LT -jev vroče vode, da končno dobite 3,43 litra tople vode pri 25 ° C.

Rešene vaje

-Vaja 2

Uveden je kos kovine 150 g mase in s temperaturo 95 ° C v posodo, ki vsebuje pol litra vode pri temperaturi 18 ° C. Čez nekaj časa je toplotno ravnovesje in temperaturo vode in kovine doseženo 25 ° C.

Recimo, da je posoda z vodo in kovinskim kosom zaprti termos, ki ne omogoča izmenjave toplote z okoljem.

Pridobite specifično toploto kovine.

Rešitev

Najprej bomo izračunali toploto, ki jo absorbira voda:

QA = Ma CA (TF - TA)

QA = 500G 1CAL/(G ° C) (25 ° C - 18 ° C) = 3500 kalorij.

To je enaka toplota, ki jo daje kovina:

QM = 150 g CM (25 ° C - 95 ° C) = -3500 kalorij.

Nato lahko dobimo toplotno zmogljivost kovine:

Cm = 3500 cal/ (150g 70 ° C) = ⅓ cal/ (g ° C).

Vaja 3

Imate 250 C.c. vode pri 30 ° C. Za tisto vodo, ki je v izolacijskem termosu, je dodanih 25 g ledenih kock pri 0 ° C z namenom, da jo ohladi.

Določite ravnotežno temperaturo; Se pravi, temperatura, ki bo ostala, ko se bo ves led stopil, in ledena voda se segreje, dokler ni voda, ki je sprva imela kozarec.

Rešitev 3

To vajo lahko rešite v treh fazah:

1. Prva je zlitje ledu, ki absorbira toploto od začetne vode, da se tali in postane voda.
2. Potem se izračuna znižanje temperature v začetni vodi, ker je dal toploto (Qced<0) para fundir el hielo.
3. Končno mora biti staljena voda (z ledu) toplotno uravnotežena z vodo, ki je sprva obstajala.

Slika 4. Vaja 3 rešitev. Vir: Self Made.

Izračunamo toploto, potrebno za zlitje ledu:

Qf = l * mH = 333,5 kJ/kg * 0,025kg = 8,338 kJ

Nato je toplota, ki jo voda dodeli za taljenje ledu, qced = -qf

Ta toplota, ki jo dodeli voda, se spusti svojo temperaturo na vrednost t ', ki jo lahko izračunamo na naslednji način:

T '= t0 - qf/(ma*ca) = 22,02 ° C

Kjer je CA toplotna zmogljivost vode: 4,18 kJ/(kg ° C).

Končno bo prvotna masa vode, ki je zdaj pri 22,02 ° C.

Končno bo ravnotežna temperatura dosežena po dovolj časa:

Te = (ma * t ' + mH * 0 ° C) / (ma + mH) = (0,25kg * 22,02 ° C + 0,025kg * 0 ° C) / (0,25kg + 0,025kg).

Končno pridobimo ravnotežno temperaturo:

Te = 20,02 ° C.

-Vaja 4

0,5 kg svinčevega kosa zapusti pečico pri temperaturi 150 ° C, kar je precej pod njeno tališče. Ta kos je nameščen v posodo s 3 litri vode pri sobni temperaturi 20 ° C. Določite končno ravnotežno temperaturo.

Izračunajte tudi:

- Količina toplote, ki jo dostavlja svinca v vodo.

- Količina toplote, ki jo absorbira voda.

Podatki:

Specifična svinčena toplota: CP = 0,03 apno/(g ° C); Specifična toplota vode: CA = 1 apno/(g ° C).

Rešitev 

Na prvem mestu določimo končno ravnotežno temperaturo TE:

Te = (ma ca ta + mp cp tp) / (ma ca + mp cp)

Te = 20,65 ° C

Potem je količina toplote, ki jo dodeli svinca,:

QP = MP CP (TE - TP) = -1.94 x 10³.

Količina toplote, ki jo absorbira voda, bo:

Qa = ma ca (te - ta) = +1,94x 10³ apno.

Reference

1. Atkins, str. 1999. Fizikalna kemija. Omega izdaje.
2. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
3. Giancoli, d. 2006. Fizika: načela z aplikacijami. 6. ... Ed Prentice Hall.
4. Hewitt, Paul. 2012. Konceptualna fizikalna znanost. 5. Ed. Pearson.
5. Resnick, r. (1999). Fizično. Vol. 1. 3. izd. v španščini. Continental uredništvo s.Do. od c.V.
6. Rex, a. 2011. Osnove fizike. Pearson.
7. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.
8. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.