Formule in enačbe rotacijskega ravnovesja, primeri, vaje

Trdi se, da je razširjeno telo rotacijsko ravnovesje Ko je vsota navora, ki delujejo na njem. To ne pomeni, da je predmet nujno v mirovanju, temveč da ni neto trenda, da bi svoje stanje gibanja spremenil v drugega.

Predmet, ki se premika s konstantno hitrostjo, to naredi po ravni črti in ga lahko upoštevamo v rotacijskem ravnovesju. Zdaj se predmeti vrtijo, ker obstajajo sile, ki delujejo nanje tako, da gre za rotacijo. Sposobnost sile, da proizvaja vrtenje, imenovano navora oz Torca, Odvisno ni samo od intenzivnosti sile, ampak tudi tam, kjer se uporablja.

Slika 1. Vzmeteni most slike je bil zasnovan tako, da je v rotaciji. Vir: Wikimedia Commons.

To prepoznamo takoj, ko se bodo odprla zaprta vrata: sila se nikoli ne nanese blizu tečajev, ampak daleč od njih, zato je ročaj nameščen, kolikor je mogoče, ob vratih vrat.

Tečaji prehajajo os vrtenja vrat. Če vztrajate, da ga potisnete zelo blizu tečajev, se morate veliko potruditi, da se vrata sploh malo premaknejo.

V literaturi je navor z različnimi imeni: trenutek torzije, torzije, trenutek sile in Torca. Vsi so sinonimi.

Torej, poznati moramo navora, ki delujejo na predmet, da vzpostavijo stanje vrtenja.

[TOC]

Stanje rotacijskega ravnovesja

Stanje rotacijskega ravnovesja je:

Vsota vseh trenutkov ali navorov, ki delujejo na telo, izračunani glede na katero koli osi, mora biti praznina.

Zadevni objekt mora biti podaljšan, saj imajo delci po definiciji le prevajalsko ravnovesje.

Lahko vam služite: Newtonov drugi zakon: aplikacije, poskusi in vaje

Na telesu se lahko uporabljajo sile in še vedno obstaja rotacijsko ravnovesje, medtem ko sile ne obrnejo.

Lahko pride tudi do gibanja, celo pospešeno, vendar vedno vzdolž ravne črte, saj vse sile ne povzročajo videza navora. Te se pojavijo, ko sile ne delujejo po isti akciji.

Navor ali trenutek sile

Navor je označen z grškimi besedili τ, v Krepka pisava Ker je vektor in ga ločimo od njegove velikosti ali modula, ki je skalar. Odvisno je od uporabljene sile F, vektorja r ki je usmerjena iz osi vrtenja ali do točke uporabe sile in na koncu kota med tema dvema vektorjem.

Pravilna povezava med temi velikosti se vzpostavi prek vektorskega izdelka:

τ = r x F

In modul navora, označen brez krepkega, je:

τ = r⋅f⋅sen θ

Kjer je θ kot med r in F. Enote navora so preprosto N⋅M v mednarodnem sistemu.

Na sliki je angleški ključ, s katerim je namenjen. Za to se preizkusi dve sili F_Do in F_B.

F_Do je bližje O in ima vektor r_Do ali krajša roka ročice, zato ne daje toliko navora in sile F_B, Ki ima enako velikost, vendar ima vektor r_B večji.

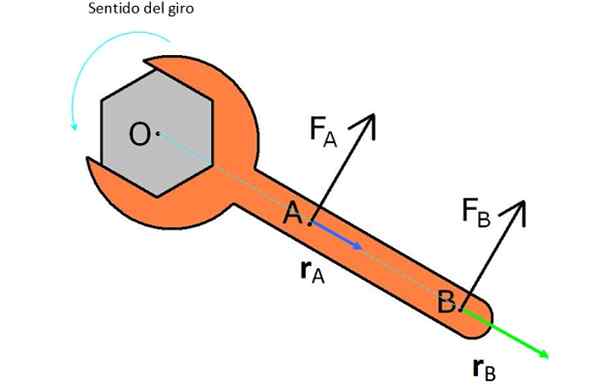Slika 2. Sile in roke, nanesene na angleški ključ, da ga obrnejo v nasprotju z iglami ure. Vir: Wikimedia Commons.

Če želite matico zasukati v urniku, morate sile uporabiti v nasprotni smeri, kako se pojavijo na sliki.

Smer in občutek navora

Ker je navor izdelka med vektorji moči in položaja, ki so v ravnini angleškega ključa, mora biti navor vektor, pravokoten na to ravnino, torej usmerjeno proti bralcu ali znotraj strani.

Vam lahko služi: atmosferski tlak: normalna vrednost, kako se meri, primeri

S konvencijo je navor pozitiven, če povzroči obračanje v nasprotni smeri igle ure, in negativno, če to stori v smeri ure.

Smer in smer nastalega navora zlahka določita pravilo desne roke, prikazane spodaj:

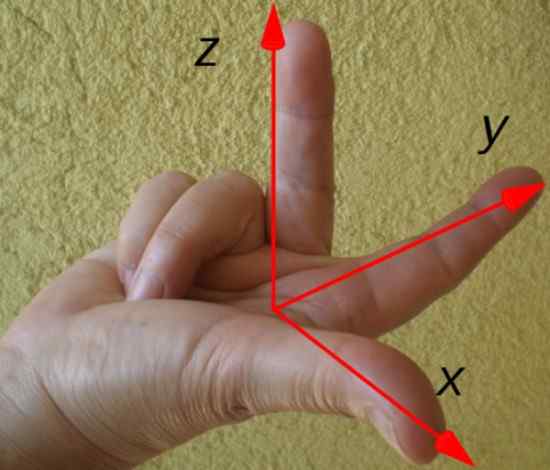Slika 3. Desno pravilo za določitev smeri in smeri troca. Vir: Wikimedia Commons.

Kazalo s prstom v skladu z vektorjem položaja r, Srednji prst glede na silo F In palec signalizira smer in smer navora τ. V tem primeru je navor usmerjen vzdolž osi x, glede na risbo koordinatnih osi.

Formule in enačbe

Če navori delujejo na telesu τ₁, τ_2, τ_{3 ..} τ_Yo, Mreža ali nastali navora τ_n To je vektorska vsota vseh:

τ_n = τ₁+ τ₂ +  τ₃ +_.. τ_Yo

S povzetkom seštevanja ostaja:

τ_n = ∑ τ_Yo

Ravnotežni pogoj je matematično izražen na naslednji način:

τ_n = 0

O No:

∑ τ_Yo = 0

Kjer navor τ, Glede določene osi O jo izračuna::

τ = r x F

In katerih velikost je:

τ = r⋅f⋅sen θ

Primeri

-Pri ljudeh in živalih je teža sila, ki lahko povzroči navor in se obrne in pade.

Ljudje običajno vzdržujejo takšen položaj, da jih pri hoji ohranjajo v ravnovesju med vrtenjem, razen če se izvajajo športna dejavnost, na primer gimnastika, drsanje ali šport na splošno.

-Dva otroka, ki ji je uspelo ostati vodoravno v rocker tudi gor in dol So v vrtenju.

-Ko so krožniki ravnotežja uravnoteženi, je sistem v rotacijskem ravnovesju.

-Obvestila in semaforji, ki visijo na ulicah in možnostih, so tudi v rotacijskem ravnovesju. Če so kabli, ki jih držijo, porušeni, se to ravnovesje izgubi in obvestilo visi ali pade.

Lahko vam služi: povprečni pospešek: kako se izračuna in reši

-Viseči mostovi, kot sta Golden Gate v San Franciscu in most slike 1.

Vaja rešena

Vrstica, podprta s podporo, prikazana na sliki, je zelo lahka. Sila, ki jo izvaja podpora F in na koncu velja sila Do.

Zahteva se, da izračunajo veličine teh sil, če upoštevamo, da je sistem v ravnovesju prevajanja in vrtenja.

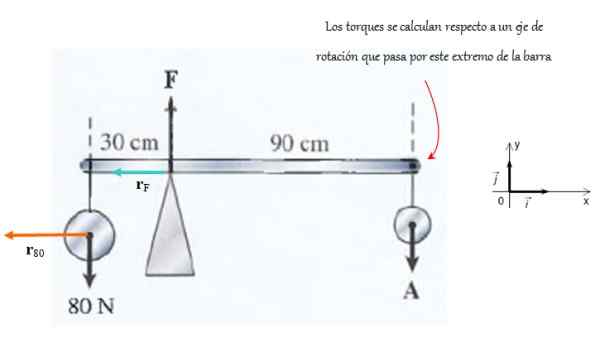Slika 4. Na tej vrstici sile delujejo tako, da ostane v rotacijskem ravnovesju. Vir: f. Zapata.

Rešitev

Ker se sistem ne premika, se vsota sil prekliče. Vsi so navpični in lahko delate z veličimi. Pozitiven smisel je naraščajoč in negativno navzdol, torej:

F - 80 - a = 0

Zdaj je uporabljen rotacijski ravnotežni pogoj, za katerega morate izbrati poljubno rotacijsko os. V tem primeru je izbran na koncu, tako da vektor r_Do Bodite ničelni, na ta način je navor, ki ga izvaja Do, ampak samo tisti F in moč levice.

Navor, ki ga je ustvaril F Glede na pravilo desne roke in prikazan koordinatni sistem:

τ_F = r_F x F = 0.9 F (-k) N.m

Je usmerjena na zaslon in ima negativni znak. Medtem ko je navor, ki ga ustvari sila 80 N,:

τ = 80 x 1.dvajset (k) N⋅m = 96 (k) N⋅m

Ta navor je usmerjen iz zaslona in je dodeljen pozitiven znak. Ker obstaja rotacijsko ravnovesje:

96 - 0.9⋅F = 0

Velikost F je:

F = (96/0.9) n = 106.7 n

In ker je sistem v prevodnem ravnovesju, se vsota sil prekliče. To nam omogoča, da razčistimo velikost Do:

F - a - 80 n = 0

Zato:

A = 106.7 - 80 n = 26.7 n.

Reference

1. Rex, a. 2011. Osnove fizike. Pearson.
2. Serway, r., Jewett, J. (2008). Fizika za znanost in inženiring. Zvezek 1. 7. Ed. Cengage učenje.
3. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1. Pearson.
4. Tipler, str. (2006) Fizika za znanost in tehnologijo. 5. izd. Zvezek 1. Uredništvo se je vrtelo.
5. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. McGraw Hill.