Gibbs proste energijske enote, kako se izračuna, rešijo vaje

The Gibbs brez energije (Običajno ga imenujemo g) je termodinamični potencial, ki je opredeljen kot razlika v entalpiji H, razen produkta temperature T, z entropijo sistema:

G = h - t s

Gibbs brezplačna energija se meri v Joulesu (po mednarodnem sistemu), v Ergiosu (za sistem lige enot), v kalorijah ali elektronskih voltih (Za elektro volte).

Slika 1. Diagram, ki prikazuje opredelitev Gibbsove energije in njenega odnosa z drugimi termodinamičnimi potenciali. Vir: jedrska moč.mreža.

V procesih, ki se pojavljajo pri konstantnem tlaku in temperaturi, je variacija Gibbsove proste energije ΔG = ΔH - t ΔS. V takšnih procesih (g) predstavlja energijo, ki je na voljo v sistemu, ki lahko postane delo.

Na primer, v eksotermičnih kemičnih reakcijah se entalpija zmanjša, medtem ko se entropija povečuje. V funkciji Gibbs se ta dva dejavnika preprečita, vendar le, ko Gibbsova energija zmanjša reakcijo spontano.

Torej, če je variacija G negativna, je postopek spontan. Ko funkcija Gibbs doseže svoj minimum, sistem doseže stabilno ravnovesje. Skratka, v postopku, za katerega tlak in temperatura ostaneta konstantna, lahko pritrdimo:

- Če je postopek spontan, potem ΔG < 0

- Ko je sistem v ravnovesju: ΔG = 0

- V ne-spontanem procesu se poveča: ΔG> 0.

[TOC]

Kako se izračuna?

Gibbs prosta energija (g) se izračuna po definiciji, podani na začetku:

G = H - T⋅s

Entalpija H je termodinamični potencial, opredeljen kot:

H = u + p v

- Korak za korakom

Nato bo narejena korak -korak za korak, da bi poznali neodvisne spremenljivke, katerih funkcija je Gibbs Energy:

1- Prvega zakona termodinamike je notranja energija povezana z entropijo sistema in njegovim volumnom V za reverzibilne procese z diferencialnim odnosom:

Lahko vam služi: etidijev bromid: struktura, lastnosti, uporabe, strupenost

du = dq - dw = tds - pdv

Iz te enačbe izhaja, da je notranja energija U funkcija spremenljivk S in V:

U = u (s, v)

2- Začen je iz definicije H in jemanje diferenciala dobimo:

dh = du + d (p v) = du + vdp + pdv

3- Nadomestitev izraza za DU, pridobljeno v (1), morate:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Od tu je sklenjeno, da je entalpija H odvisna od entropije S in tlaka P, to je:

H = h (s, p)

4- Zdaj se izračuna skupna diferencial Gibbs proste energije, ki dobi:

Dg = dh -tds -sdt = tds + vdp -tds -sdt

Kjer je DH nadomeščen z izrazom, ki ga najdemo v (3).

5- Končno s poenostavitvijo dobite: DG = VDP - SDT, Jasno je, da je prosta energija g odvisna od tlaka in temperature t kot:

G = g (p, t)

- Maxwellovi termodinamični odnosi

Iz analize v prejšnjem razdelku izhaja, da je notranja energija sistema funkcija entropije in volumna:

U = u (s, v)

Potem diferencial Ali biti:

du = ∂_SU |_V DS + ∂_VU |_S DV = TDS - PDV

Iz tega izraza v delnih derivatih lahko sklepamo tako imenovani Maxwell termodinamični razmerji. Delni derivati ​​veljajo, kadar je funkcija odvisna od več kot ene spremenljivke in jih je enostavno izračunati z uporabo teorema naslednjega razdelka.

Maxwellovo prvo razmerje

 ∂_VT |_S = -Mon_SP |_V 

Da bi prišli do tega odnosa, Teorem Clairaut - Schwarz o delnih derivatih, ki navajajo naslednje:

"Mešani derivati ​​drugega reda z izmenjanimi spremenljivkami so enaki, pod pogojem, da so funkcije, ki jih je treba izpeljati, neprekinjene in razlike".

Maxwellovo drugo razmerje

Začenši iz tistega, kar je bilo dokazano v točki 3 prejšnjega oddelka:

Vam lahko služi: dejavniki, ki vplivajo na topnost

H = H (s, P) in DH = TDS + VDP

Lahko dobimo:

 ∂_StrT |_S = ∂_SV |_Str 

Nadaljujte na podoben način z Gibbs Free Energy G = g (p, t) in s prostim energijam Helmholtza F = f (t, v) Pridobiti druga dva termodinamična razmerja Maxwella. 

Slika 2. Josiah Gibbs (1839-1903) je bil ameriški fizik, kemik in matematik, ki je veliko prispeval k termodinamiki. Vir: Wikimedia Commons.

Maxwellovi štirje termodinamični odnosi 

1- povezan z notranjo energijo U: ∂_VT |_S = -Mon_SP |_V

2- Tisti, pridobljeni iz entalpije H: ∂_StrT |_S = ∂_SV |_Str 

3- Povezano z energijo Helmholtza F: ∂_TP |_V = ∂_VS |_T 

4- Povezano s prostim energijam Gibbs G: ∂_TV |_Str = -Mon_StrS |_T

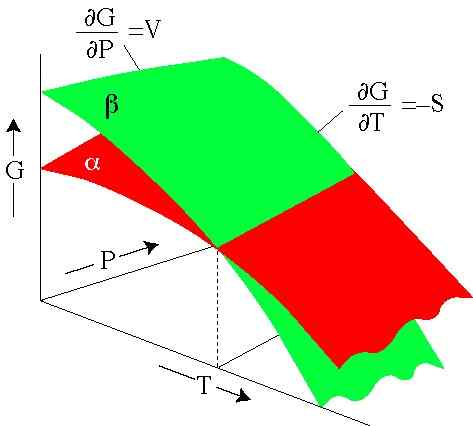Slika 2. Gibbsova energija je odvisna od tlaka in temperature. Vsaka površina predstavlja fazo. (SERC.Carleton.Edu)

Rešene vaje

Vaja 1

Izračunajte variacijo Gibbs proste energije za 2 mola idealnega plina pri temperaturi 300K med izotermalno širitvijo, ki vodi do začetnega volumskega sistema 20 litrov do končne prostornine 40 litrov.

Rešitev

Spominjanje definicije Gibbs Free Energy je:

G = h - t s

Potem bo končna sprememba F:

ΔG = ΔH - t ΔS, Ker ΔT = 0

V idealnih plinih je entalpija odvisna le od njegove absolutne temperature, vendar ker gre za izotermalni postopek, potem ΔH = 0 in ΔG = - t ΔS.

Za idealne pline je entropijska variacija izotermalnega procesa: 

ΔS = nr ln (v₂/V₁)

To velja za primer te vaje:

ΔS = 2 mola x 8,314 j/(k mol) x ln (40L/20L) = 11,53 j/k

Potem lahko dobimo spremembo v Helmholtzovi energiji:

ΔG = - 300K x 11,53 j/k = -3457,70 j.

Vaja 2

Ob upoštevanju, da je Gibbs prosta energija funkcija temperature in tlaka g = g (t, p); Določite variacijo G med postopkom, v katerem se temperatura ne spreminja (izotermalno) za N mole idealnega monoatomskega plina.

Vam lahko služi: stroncijev hidroksid (sr (OH) ₂)

Rešitev

Kot je prikazano zgoraj, je sprememba Gibbsove energije odvisna le od spremembe temperature T in volumna V, zato se neskončno majhna variacija izračuna v skladu z:

Dg = -sdt + vdp

Če pa gre za postopek, v katerem je temperatura konstantna, potem df = + VDP, torej končna sprememba tlaka ΔP vodi do spremembe Gibbsove energije, ki jo daje:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Z uporabo idealne enačbe plina:

P v = n r t

Med izotermalnim postopkom se zgodi:

D (p v) = p dv + v dp = 0

To je:

dp/p = - dv/v

Torej lahko prejšnji rezultat zapišemo, odvisno od sprememb glasnosti ΔV:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (ΔV)

Vaja 3

Glede na naslednjo kemijsko reakcijo:

N₂0 (g) + (3/2) oz₂ (g) ↔️no₂ (g) pri temperaturi t = 298 k

Poiščite variacijo Gibbs brez energije in s pridobljenim rezultatom navedite, ali gre za spontani postopek ali ne.

Rešitev

Pod koraki:

- Prvi korak: reakcijske entalpije

ΔHR = 2*ΔH (št₂ (g)) - ΔH (n₂0 (g)) = 2*33.2-81.6 = -15.2kJ/mol

- Drugi korak: Sprememba entropije reakcije

ΔSr = 2*s (ne₂ (g)) - s (n₂0 (g)) - (3/2) s (ali₂ (g)) = 2*240.1 - 220.1 - 1,5*205.2 = -47,7 j/(mol*k).

- Tretji korak: Sprememba funkcije Gibbs

Ta vrednost bo določila ravnovesje med zmanjševanjem energije in povečanjem entropije, da vemo, ali je reakcija končno spontana ali ne.

ΔGr = ΔHR -T ΔSR = -15,2 -298*(-47,7) = -985,4 j/mol

Ker gre za negativno variacijo Gibbsove energije, je mogoče sklepati, da gre za spontano reakcijo pri temperaturi 298 K = 25 ° C.

Reference

1. Castaños e. Proste energijske vaje. Okrevano od: lidiaconlachimica.WordPress.com.
2. Cengel in. 2012. Termodinamika. 7. izdaja. McGraw Hill.
3. Librettexts. Gibbs brez energije. Okrevano od: kem.Librettexts.org
4. Librettexts. Kaj je brezplačna energija. Okrevano od: kem.Librettexts.org
5. Wikipedija. Gibbs brez energije. Okrevano od: je.Wikipedija.com
6. Wikipedija. Gibbs brez energije. Pridobljeno iz: v.Wikipedija.com