Polinomne enačbe

Kaj so polinomne enačbe?

The Polinomne enačbe To so izjava, ki dviguje enakost dveh izrazov ali članov, kjer so vsaj eden od izrazov, ki sestavljajo vsako stran enakosti, polinomi p (x). Te enačbe so poimenovane glede na stopnjo njihovih spremenljivk.

Na splošno je enačba izjava, ki vzpostavlja enakost dveh izrazov, kjer vsaj v enem od teh obstajajo neznane količine, ki se imenujejo spremenljivke ali neznane. Čeprav obstaja veliko vrst enačb, so te na splošno razvrščene v dve vrsti: algebrski in transcendentni.

Polinomske enačbe vsebujejo samo algebrske izraze, ki imajo lahko eno ali več neznank, ki posegajo v enačbo. Glede na eksponento (oceno), ki jo imajo, jih je mogoče razvrstiti med: prvi razred (linearni), drugi razred (kvadratni), tretji razred (kubični), četrti razred (quantic), stopnje, večje ali enake pet in pet in iracionalno.

Značilnosti polinomnih enačb

Polinomne enačbe so izrazi, ki tvorijo enakost med dvema polinomoma; Torej za končne vsote množenja med neznanimi vrednostmi (spremenljivkami) in fiksnimi številkami (koeficienti), kjer imajo spremenljivke lahko eksponente, njihova vrednost pa je lahko pozitivno celo število, vključno z ničlo.

Eksponenti določajo stopnjo ali vrsto enačbe. Ta izraz izraza, ki ima največ vrednosti, bo predstavljal absolutno stopnjo polinoma.

Polinomne enačbe so znane tudi kot algebrski, njihovi koeficienti so lahko resnične ali zapletene številke, spremenljivke pa so neznane številke, ki jih predstavlja črko, kot je: "x".

Če z zamenjavo vrednosti s spremenljivko "x" v p (x) je rezultat enak nič (0), potem se reče, da ta vrednost izpolnjuje enačbo (je rešitev) in se na splošno imenuje polinomna korenina.

Ko se razvije polinomna enačba, želijo najti vse korenine ali rešitve.

Vrste polinomnih enačb

Obstaja več vrst polinomnih enačb, ki se razlikujejo glede na število spremenljivk in tudi glede na stopnjo njihove eksponent.

Tako so polinomne enačbe -kjer je njegov prvi izraz polinom, ki ima le en neznan, če upoštevamo, da je njegova stopnja lahko naravno število (n), drugi izraz pa je nič -lahko izražen na naslednji način:

Vam lahko služi: Zgodovina trigonometrije iz njegovega izvora

do_{N *} xⁿ + do_{N-1 *} x^N-1 +… + A_{1 *} x¹ + do_{0 *} x₀ = 0

Kje:

• do_n, do_N-1 že₀, So resnični koeficienti (številke).
• do_n je drugačen od nič.
• Exponent N je pozitivno število, ki predstavlja stopnjo enačbe.
• x je spremenljivka ali neznana, ki jo je treba iskati.

Absolutna ali večja stopnja polinomne enačbe je tista, ki je večja vrednost med vsemi tistimi, ki tvorijo polinom; Na ta način so enačbe razvrščene kot:

Prva ocena

Polinomne enačbe prve stopnje, znane tudi kot linearne enačbe, so tiste, na katere je stopnja (največji eksponent) enaka 1, polinom je oblike p (x) = 0; In je sestavljen iz linearnega in neodvisnega izraza. Napisano je na naslednji način:

AX + B = 0.

Kje:

• A in B sta resnični številki in A ≠ 0.
• AX je linearni izraz.
• B je neodvisen izraz.

Na primer, enačba 13x - 18 = 4x.

Za reševanje linearnih enačb je treba vse izraze, ki vsebujejo neznano x, prenesti na stran enakosti in tisti, ki se ne premikajo na drugi strani, da bi jo očistili in pridobili rešitev:

13x - 18 = 4x

13x = 4x + 18

13x - 4x = 18

9x = 18

x = 18 ÷ 9

x = 2.

Na ta način ima dana enačba samo eno rešitev ali koren, ki je x = 2.

Drugi razred

Polinomne enačbe druge stopnje, znane tudi kot kvadratne enačbe, so tiste, pri katerih je stopnja (največji eksponent) enaka 2, polinom je oblike p (x) = 0 in je sestavljen iz kvadratnega izraza, a linearna in neodvisna. Izraženo je na naslednji način:

sekira² + bx + c = 0.

Kje:

• a, b in c so realne številke in a ≠ 0.
• sekira² To je kvadratni izraz in "A" je koeficient kvadratnega izraza.
• BX je linearni izraz in "B" je koeficient linearnega izraza.
• C je neodvisen izraz.

Odločnost

Na splošno je rešitev te vrste enačb podana pri čiščenju x enačbe in ostane na naslednji način, ki se imenuje odločitev:

Vam lahko služi: Binomialni teorem

Tam, (b² - 4ac) se imenuje diskriminatorno iz enačbe in ta izraz določa število rešitev, ki jih ima enačba:

• Da (b² - 4ac) = 0, enačba bo imela eno samo rešitev, ki je dvojna; to pomeni, da bo imela dve enaki rešitvi.
• Da (b² - 4ac)> 0, enačba bo imela dve različni resnični rešitvi.
• Da (b² - 4AC) < 0, la ecuación no tiene solución (tendrá dos soluciones complejas distintas).

Na primer, imate 4x enačbo² + 10x - 6 = 0, če ga najprej rešimo, se identificirajo izrazi A, B in C, nato pa jih zamenjajo v formuli:

A = 4

B = 10

C = -6.

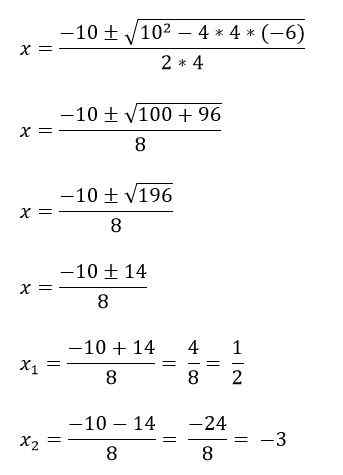
Obstajajo primeri, v katerih polinomne enačbe drugega stopinj nimajo treh izrazov, zato se rešijo drugače:

• V primeru, da kvadratne enačbe nimajo linearnega izraza (to je b = 0), bo enačba izražena kot sekira² + C = 0. Da bi ga rešili, se x očisti² In v vsakem članu se uporabljajo kvadratne korenine in se spomnijo, da imata dva možna znaka, da imata neznano:

sekira² + C = 0.

x² = - C ÷ a

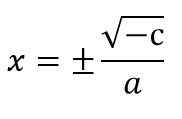
Na primer 5 x² - 20 = 0.

5 x² = 20

x² = 20 ÷ 5

x = ± √4

x = ± 2

x₁ = 2.

x₂ = -2.

• Ko kvadratna enačba nima neodvisnega izraza (to je C = 0), bo enačba izražena kot sekira² + Bx = 0. Za reševanje je treba v prvem članu vzeti skupni dejavnik neznanega X; Ker se enačba ujema z ničlo, je izpolnjeno, da bo vsaj eden od dejavnikov enak 0:

sekira² + Bx = 0.

x (ax + b) = 0.

Na ta način morate:

x = 0.

x = -b ÷ a.

Na primer: imate enačbo 5x² + 30x = 0. Najprej je dejavnik:

5x² + 30x = 0

x (5x + 30) = 0.

Ustvarjena sta dva dejavnika, ki sta x y (5x + 30). Eden od teh bo obravnavan kot nič, druga pa je rešitev:

x₁ = 0.

5x + 30 = 0

5x = -30

x = -30 ÷ 5

x₂ = -6.

Najvišja ocena

Glavne stopnje polinomne enačbe so tiste, ki segajo od tretjega razreda naprej, ki jih je mogoče izraziti ali rešiti s splošno polinomno enačbo za katero koli stopnjo:

Vam lahko služi: koeficient korelacije: formule, izračun, razlaga, primer

do_{N *} xⁿ + do_{N-1 *} x^N-1 +… + A_{1 *} x¹ + do_{0 *} x₀ = 0

To se uporablja, ker je enačba s stopnjo, večjo od dveh, posledica faktorizacije polinoma; to pomeni, da je izraženo kot množenje prve ali večje stopnje, vendar brez resničnih korenin.

Rešitev te vrste enačb je neposredna, ker bo množenje dveh dejavnikov enako nič, če je kateri koli od dejavnikov ničen (0); Zato je treba vsako od najdenih polinomnih enačb rešiti, kar ustreza vsakemu od njegovih dejavnikov na nič.

Na primer, imate enačbo tretje stopnje (kubični) x³ + x² +4x + 4 = 0. Če ga želite rešiti, morate slediti naslednjim korakom:

• Pogoji so razvrščeni:

x³ + x² +4x + 4 = 0

(x³ + x² ) + (4x + 4) = 0.

• Člani se pokvarijo, da bi dobili skupni dejavnik neznanega:

x² (x + 1) + 4 (x + 1) = 0

(x² + 4)_*(x + 1) = 0.

• Na ta način se dobita dva dejavnika, ki morata biti enaka nič:

(x² + 4) = 0

(x + 1) = 0.

• Vidimo, da je faktor (x² + 4) = 0 ne bo imel prave rešitve, medtem ko faktor (x + 1) = 0 da. Zato je rešitev:

(x + 1) = 0

x = -1.

Rešene vaje

Rešite naslednje enačbe:

Prva vaja

(2x² + 5)_*(X - 3)_*(1 + x) = 0.

Rešitev

V tem primeru je enačba izražena kot množenje polinomov; to pomeni, da je faktorizirano. Za reševanje mora biti vsak faktor enak nič:

2x² + 5 = 0, nima rešitve.

x - 3 = 0

x = 3.

1 + x = 0

x = - 1.

Na ta način ima dana enačba dve rešitvi: x = 3 in x = -1.

Druga vaja

x⁴ - 36 = 0.

Rešitev

Podani je bil polinom, ki ga je mogoče odpisati kot razlika v kvadratih, da dosežemo hitrejšo raztopino. Tako enačba ostaja:

(x² + 6)_*(x² - 6) = 0.

Za iskanje rešitve enačb sta oba dejavnika enaka nič:

(x² + 6) = 0, nima rešitve.

(x² - 6) = 0

x² = 6

x = ± √6.

Tako ima začetna enačba dve rešitvi:

x = √6.

x = - √6.