Delne enačbe

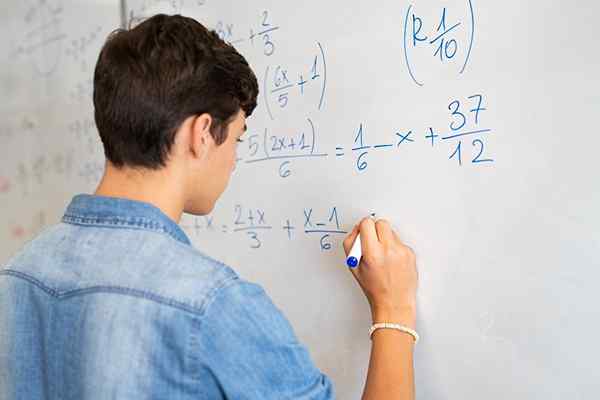Delne enačbe vključujejo numerične in/ali algebrske frakcije, neznano

Kaj so frakcijske enačbe?

The Delne enačbe so tisti, ki vsebujejo frakcije v enem ali več njihovih pogojih. Takšne frakcije so lahko numerične ali algebrske, kjer je neznano mogoče najti v števcu in/ali v imenovalcu katerega koli izraza.

Nato nekaj primerov frakcijskih enačb z enim samim neznanim:

Prvi primer je linearna enačba z frakcijskimi koeficienti; V drugem primeru je neznano v imenovalcu vsakega od izrazov, v zadnjem.

Da bi jih rešili, je treba izvesti nekatere algebrske transformacije in tako pridobiti enakovredno enačbo, v kateri se neznani ne pojavljajo v imenovalcu. Ko je ta postopek izveden, rešitev najdemo z ustreznimi tehnikami.

Rešitev je sestavljena iz nabora vrednosti "x", ki izpolnjujejo enakost. Lahko je edinstvena vrednost ali več, vsekakor pa je zelo pomembno upoštevati, da niso vse rešitve v enakovredni enačbi sprejemljive za prvotno enačbo.

Dejansko, če gre za enačbo, katere neznano je v imenovalcu, vrednosti "X", ki se jih moramo izogniti. To je zato, ker delitev med 0 ni definirana.

Če ima enakovtna enačba edinstveno rešitev in izkaže se, da je imenovalec katerega koli pogoja prvotne enačbe preklican, potem nima rešitve.

Kako rešiti delno enačbo

Operacije, ki se izvajajo za reševanje nefrakcijskih enačb, so veljavne, pod pogojem, da se enakost vzdržuje. Na ta način lahko v delni enačbi dodate ali odštejete enako količino obema stranema enakosti, pomnožite vse izraze z istim zneskom ali delite vsak izraz za isti znesek (drugačen od 0).

Vam lahko služi: teorem Bolzano

Ker pa je delna enačba potrebna za preoblikovanje v drugo enakovredno brez imenovalcev, sledijo tudi naslednje splošne indikacije:

1. Poiščite minimalno skupno večkratno imenovalce (m.c.m).
2. Pomnožite vsak izraz z m.c.m., Da bi odpravili imenovalce.
3. Rešite enakovredno pridobljeno.
4. Preverite, ali najdene rešitve izpolnjujejo prvotno enakost.

Vrste enakovrednih enačb

Enakovredne enačbe, pridobljene po navedenem postopku, so lahko:

• Linearna ali prva stopnja
• Kvadratna
• Višjega reda

Rešeni primeri

Primer 1

Rešite naslednjo enačbo:

Opozoriti je, da je enačba prva stopnja v "x", saj je "x" visoka pri 1. Koeficienti enačbe so frakcije in način, da jih odpravite, za delo s celotnimi številkami, pomnoži vse izraze z najmanj večkratnimi imenovalci (m.c.m.).

m.c.m. (2,3,6) = 6

Tako:

3x - 2x = 1

x = 1

Bralec lahko preveri veljavnost te rešitve in v prvotni enačbi nadomesti x = 1 in preveri, ali je enakost dobila enakost.

Primer 2

Določite vrednosti "x", ki izpolnjujejo:

Za razliko od prejšnjega primera je v tem primeru neznano najdeno v imenovalcu. Upoštevajte, da so imenovalci razveljavljeni za vrednosti x = 2 in x = −1, podrobnost, ki jo je primerno upoštevati, saj, če enakovredna enačba prizna te rešitve, jih moramo zavreči, saj niso dopustne V prvotni enačbi.

Zdaj moramo enačbo spremeniti v drugo brez imenovalcev, prvi korak je, da vsoto izrazov postavimo levo od enakosti:

Ker so imenovalci enaki, tako da se izpolnjuje enakost, je potrebno, da so tudi števci:

Vam lahko služi: konstantna sorazmernost: kaj je, izračun, vaje

4 (x+1) - 3 (x -2) = 8

Dovolj je, da rešimo to enačbo, za katero se izkaže, da je prva ocena:

4x + 4 - 3x + 6 = 8

x = 8 - 6 - 4 = - 2

x = - 2

Ker se ta vrednost razlikuje od prepovedanih vrednosti, je priznana kot rešitev izvirne enačbe.

Primer 3

Poiščite rešitev:

V tej enačbi vrednost X = 4 prekliče imenovalce, zato je izključena iz nabora raztopine preoblikovane enačbe, če se pojavi.

Preoblikovane enačbe je enostavno najti, dovolj je, da pomnožite vse izraze s faktorjem (X-4):

Ostati:

2x - 4 = 4

2x = 8

x = 4

Primer 4

Rešite enačbo:

V tem primeru imajo imenovalci kvadratne izraze, zato jih je primerno najprej upoštevati:

• x² + 8x + 7 = (x + 7) (x + 1)
• x² - 49 = (x + 7) (x - 7)
• x² - 6x - 7 = (x - 7) (x + 1)

Enačba je takšna:

Vrednosti X, ki prekličejo katerega koli od imenovalcev, so: x = −7, x = 7, x = −1. Tudi če so te vrednosti del rešitve spremenjene enačbe, ne morejo biti rešitev prvotne enačbe.

Zdaj prihaja postopek preoblikovanja enačbe. Prvi korak je najti minimalno skupno večkratno imenovalce:

m.c.m. = (x + 7) (x - 7) (x + 1)

Z množenjem na obeh straneh enakosti z m.c.m. je ostalo:

Rezultat:

(x --7) (x - 2) = (x + 1) (2x - 5) - (x + 7) (x - 2)

S pomočjo distribucijskih lastnosti so izdelki razviti:

x² - 9x +14 = 2x² - 3x - 5 - (x² + 5x - 14)

Zmanjšanje podobnih izrazov na desni strani:

x² - 9x + 14 = x² - 8x + 9

Kvadratni pogoji se prekličejo z izpolnjevanjem istega znaka na različnih straneh enakosti:

Vam lahko služi: kocka razlika: formule, enačbe, primeri, vaje

- 9x + 14 = - 8x + 9

-x = -5 ⇒ x = 5

Ta rezultat je sprejet kot rešitev, saj ni nobena od prepovedanih vrednosti.

Uporaba izvajanja frakcijskih enačb

Imenovalec dela presega štiri enote za števce. Če se števec odšteje od števca in imenovalca, je nastala frakcija 3/5. Določite prvotno frakcijo.

Rešitev

Naj bo x vrednost števca.

Ker imenovalec frakcije presega štiri enote na števca, je originalni delež:

Zdaj morate odšteti 5 enot, tako za števca kot imenovalec:

Ker je delež, ki je posledica izvedbe prejšnjega postopka, enak 3/5, so izenačeni:

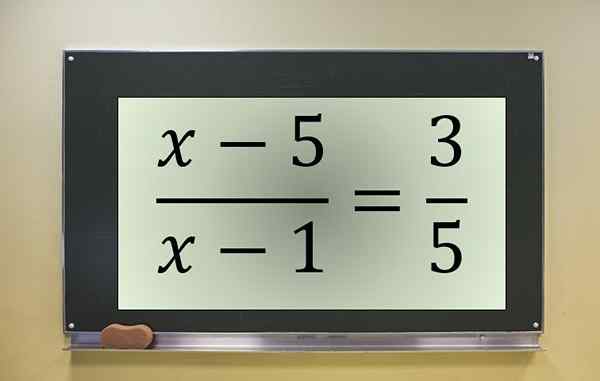Primer delne enačbe. Vir: f. Zapata.

To je frakcijska enačba z neznanim v števcu in imenovalcu, ki se prekliče pri x = 1. Zato mora biti ta vrednost izključena, če bi bila med rešitvami preoblikovane enačbe.

Nato obe strani pomnoži z minimalnim skupnim večkratnikom, ki je 5 (x - 1):

Kar ima za posledico naslednjo enakovredno enačbo:

5 (x - 5) = 3 (x - 1)

Uporaba distribucijske lastnosti:

5x -25 = 3x - 3 ⇒ 2x = 22

x = 11

Prvotna frakcija v izrazu nadomešča x = 11:

Kar ima za posledico delež 11/15. To je odgovor na sproženo težavo.

Reference

1. Delne enačbe. Okrevano od: MathePower.com
2. Portal matematike. Delne enačbe. Reševanje problemov. Okrevano od: Silvioduduarte.com.
3. Stewart, J. (2007). Predhodno: matematika za izračun. 5. Izdaja. Cengage učenje.
4. Sullivan, m. (1997). Prekalenkulacija. 4. Izdaja. Pearson Education.
5. Zill, d. (2008). Predhod z napredkom izračuna. 4. Izdaja. McGraw Hill.