Formula enačb prvega razreda, kako jih rešiti, na primer vaje

The Prva stopnja ali linearne enačbe Z neznanim so tisti, ki jih je mogoče izraziti kot vsota dveh izrazov na naslednji način:

AX + B = 0

Kje a in b, z do ≠ 0, so resnične številke r ali tudi kompleksi c. Za reševanje se izrazi prenašajo, kar pomeni spreminjanje izrazov z ene strani na drugo enakost.

Slika 1. Linearna enačba je y = mx + c obrazec z y = 0. Vir: pxhere.

Za razčiščevanje neznanega se izraz +B prenese, kar mora iti na desno stran enakosti s spremenjenim znakom.

ax = -b

Potem se na ta način očisti vrednost x:

x = - b/a

Kot primer bomo rešili naslednjo enačbo:

6x - 5 = 4

Izraz -5 prenašamo na desno stran s spremenjenim znakom:

6x = 4 + 5

To je enakovredno dodajanju 5 na obeh straneh prvotne enačbe:

6x - 5 + 5 = 4 + 5 → 6x = 9

In zdaj razčistimo neznani "x":

x = 9/6 = 3/2

Ki je enakovredno delitvi obeh strani enakosti do 6. Tako lahko ocenimo naslednje, da dobimo rešitev:

-Enako količino lahko dodate ali odštejemo obe strani enakosti v enačbi, ne da bi ga spremenili.

-Prav tako lahko pomnožite (ali delite) z istim zneskom vsem izrazom tako levo kot na desno enačbo.

-In če se oba člana enačbe dvigneta na isto moč, tudi enakost ni spremenjena.

[TOC]

Kako rešiti enačbe prve stopnje

Rešitev enačbe prve stopnje je znana tudi kot koren istega. Vrednost X pretvori izvirni izraz v enakost. Na primer v:

5x = 8x - 15

Če v tej enačbi nadomestimo x = 5, se dobi:

5⋅5 = 8⋅5 - 15

25 = 40 - 15

25 = 25

Ker so linearne enačbe prve stopnje na več načinov, ki včasih niso razvidne, obstaja vrsta splošnih pravil, ki obsegajo več algebrskih manipulacij, da bi našli vrednost neznanega:

-Najprej, če obstajajo navedene operacije, jih je treba izvesti.

-Razvrščanje simbolov, kot so oklepaji, kvadratni oklepaji in tipke, če obstajajo, je treba zatreti z vzdrževanjem ustreznih znakov.

-Izrazi se prenesejo tako, da postavijo vse, ki vsebujejo neznano na eno samo stran enakosti, in tiste, ki ga ne vsebujejo.

-Potem se vsi podobni izrazi zmanjšajo, da dosežejo obrazec ax = -b.

-In zadnji korak je razčiščevanje neznanega.

Grafična razlaga

Enačba prve stopnje, dvignjena na začetku, lahko izhajamo iz enačbe črte y = mx+c, pri čemer naredi y = 0. Vrednost x, ki rezultat ustreza presečišču črte z vodoravno osjo.

Na naslednji sliki imate tri vrstice. Začenši z zeleno črto, katere enačba je:

Vam lahko služi: faktorizacija

y = 2x - 6

Izdelava y = 0 v vrstici črte dobimo enačbo prve stopnje:

2x - 6 = 0

Katere rešitev je x = 6/2 = 3. Zdaj, ko podrobno opisujemo graf, je enostavno spoznati, da se linija dejansko zmanjša na vodoravno osi pri x = 3.

Modra črta seka os x pri x = 5, ki je rešitev enačbe -x + 5 = 0. Končno, črta, katere enačba je y = 0.5x + 2 razrezano na osi x pri x = -4, kar je enostavno opozoriti na enačbo prve stopnje:

0.5 x + 2 = 0

x = 2/0.5 = 4

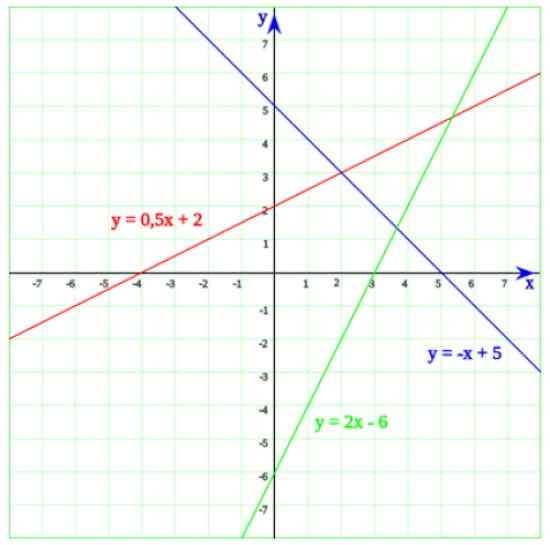Slika 2. Tri črte, katerih križišča z vodoravno osi ustrezajo linearnim enačbam. Vir: Wikimedia Commons.

Primeri preprostih linearnih enačb   

Celotne enačbe

To so tisti, v katerih na primer ni imenovalcev:

21 - 6x = 27 - 8x

Njegova rešitev je:

-6x + 8x = 27 - 21

2x = 6

x = 3

Delne enačbe

Te enačbe vsebujejo vsaj enega drugačnega imenovalca 1. Za reševanje je priporočljivo.

Naslednja enačba je frakcijski tip:

Imenovalci so 6, 8 in 12, njihov minimalni skupni večkratnik.c.M (6, 8,12) je najmanjši od številk, ki vsebujejo te imenovalce.

Ker so te številke majhne, ​​ni težko razbrati, da m.c.M (6, 8,12) = 24. Ta rezultat je enostavno dobiti z izražanjem številk kot produkta glavnih številk ali njihovih moči, poglejmo:

6 = 3.2

8 = 2³

12 = 2²⋅3

Najmanjši skupni večkratnik se določi tako, da se pomnoži skupni in neobveščeni faktorji 6, 8 in 12 z največjim eksponentom, nato pa:

MCM (6,8,12) = 2³ ⋅3 = 8 × 3 = 24

Ker je na voljo minimalni skupni večkratnik, ga je treba pomnožiti z vsakim pogojem enačbe:

Na ta način so imenovani za potlačeni in obstaja enačba z izdelki, lažje rešiti:

4 (x+5) -3 (2x+3) = 2 (1-5x)

Uporabljamo distribucijsko lastnost:

4x + 20 - 6x -9 = 2 - 10x

Vsi izrazi, ki vsebujejo neznani "X", so združeni na levo stran enakosti, pri čemer puščajo neodvisne ali številčne izraze desne strani:

4x - 6x + 10 x = 2 +9 - 20

8x = -9

x = - 9/8

Dobesedne enačbe

So linearne enačbe z neznanim, ki jih spremljajo dobesedni koeficienti (črke). Te črke se obravnavajo tako, kot bi bilo to storjeno s številkami. Primer dobesedne enačbe prve stopnje je:

-3ax + 2a = 5x - b

Ta enačba je rešena na enak način, kot če bi bili neodvisni izrazi in koeficienti številčni:

-3ax - 5x = - b - 2a

Faktor neznanega "x":

x (-3a - 5) = - b - 2a

x = ( - b - 2a) / (-3a - 5) → x = (2a + b) / (3a + 5)

Sistemi enačb prve stopnje 

Sistemi enačb so sestavljeni iz nabora enačb z dvema ali več neznankami. Sistemska rešitev je sestavljena iz vrednosti, ki izpolnjujejo enačbe hkrati in da jo nedvoumno določijo, mora obstajati enačba za vsako neznano.

Vam lahko služi: vektorska algebra

Splošna oblika sistema m Linearne enačbe z n Neznanke so:

do_enajstx₁ + do₁₂x₂ +… Do_1Nx_n = b₁
do_enaindvajsetx₁ + do₂₂x₂ +… Do_2Nx_n = b₂
..
do_M1x₁ + do_m2x₂ +… Do_mnx_n = b_m

Če ima sistem rešitev, se reče, da je določeno združljivo, Ko je neskončen niz vrednot, ki ga izpolnjujejo nedoločeno združljivo, In končno, če nima rešitve, potem je nezdružljivo.

Pri ločljivosti sistemov linearnih enačb se uporablja več metod: zmanjšanje, zamenjava, izenačenje, grafične metode, Gauss-Jordana izločanje in uporaba dejavnikov so med najbolj uporabljenimi. Vendar obstajajo drugi algoritmi za dosego rešitve, bolj priročni za sisteme z veliko enačb in neznanimi.

Primer sistema linearnih enačb z dvema neznankoma je:

8x - 5 = 7y - 9
6x = 3y + 6

Rešitev tega sistema se predloži pozneje v razdelku Rešene vaje.

Linearne enačbe z absolutno vrednostjo

Absolutna vrednost realne številke je razdalja med njeno lokacijo na številčni črti in 0 istega. Je razdalja njena vrednost je vedno pozitivna.

Absolutna vrednost številke je označena z modulskimi palicami: │x│. Absolutna vrednost pozitivnega ali negativnega števila je vedno pozitivna, na primer:

│+8│ = 8

│-3│ = 3

V enačbi z absolutno vrednostjo je neznano med modulskimi palicami. Razmislite o naslednji preprosti enačbi:

│x│ = 10

Obstajata dve možnosti, prva je, da je X pozitivno število, v tem primeru pa imamo:

x = 10

In druga možnost je, da je X v tem primeru negativna številka:

x = -10

To so rešitve te enačbe. Zdaj pa si oglejmo drugačen primer:

│x+6│ = 11

Znesek znotraj palic je lahko pozitiven, potem pa:

x+6 = 11

x = 11 -6 = 5

Ali je lahko negativen. V tem primeru:

-(x+6) = 11

-x - 6 = 11 ⇒ -x = 11+6 = 17

In vrednost neznanega je:

x = -17

Ta enačba absolutne vrednosti ima torej dve rešitvi: x₁ = 5 in x₂ = -17. Preverimo lahko, da obe rešitvi vodita do enakosti v prvotni enačbi:

│5+6│ = 11

│11│ = 11

In

│-17+6│ = 11

│-11│ = 11

Preproste rešene vaje

- Vaja 1

Rešite naslednji sistem linearnih enačb z dvema neznankoma:

8x - 5 = 7y -9
6x = 3y + 6

Rešitev

Ker je ta sistem dvignjen, je primeren za uporabo metode zamenjave, saj v drugi enačbi neznano x Skoraj pripravljen je za čiščenje:

x = (3y + 6)/6

Vam lahko služi: algebrski

In takoj lahko zamenjate prvo enačbo, ki nato postane prva enačba z neznanim "Y":

8 [(3y + 6)/6] - 5 = 7y - 9

Imenovalec je mogoče zatreti, če se vsak izraz pomnoži s 6:

6 . 8⋅ [(3y + 6)/6] - 6.5 = 6 .7y- 6 . 9

8⋅ (3y + 6) - 30 = 42y - 54

Uporaba distribucijske lastnosti v prvem mandatu za pravico do enakosti:

24y + 48 -30 = 42y - 54 ⇒ 24y + 18 = 42y - 54

Enačbo je mogoče poenostaviti, saj so vsi koeficienti večkratniki 6:

4y + 3 = 7y - 9

-3y = -12

y = 4

S tem rezultatom gremo na odmik X:

x = (3y +6)/6 → x = (12 +6)/6 = 3

- Vaja 2

Rešite naslednjo enačbo:

Rešitev

V tej enačbi se pojavijo izdelki in po navodilih, ki so jih dali na začetku, jih je treba najprej razviti:

3x - 10x +14 = 5x + 36x + 12

Potem se vsi izrazi, ki vsebujejo neznanke, prenesejo na levo stran enakosti, na desni strani pa bodo neodvisni izrazi:

3x - 10x - 5x - 36x = 12 - 14

-48x = -2

x = 1/24

- Vaja 3

Z dodajanjem treh notranjih kotov trikotnika dobimo 180 °. Največji presega otroka v 35 °, kar posledično presega 20 ° razlika med največjo in srednjo. Kakšni so koti?

Rešitev

Poklicali bomo "x" do glavnega kota, "y" do medija in "z" otroku. Ko izjava navaja, da je vsota le -teh 180 °, lahko napišete:

x + y + z = 180

Potem vemo, da najstarejši presega otroka v 35 °, to lahko napišemo:

X = z + 35

Končno otrok preseže 20 ° do razlike med največjo in srednjo:

Z = x - y + 20

Imamo sistem treh enačb in 3 neznanke:

x + y + z = 180

X = z + 35

Z = x - y + 20

S čiščenjem prve enačbe imate:

Z = 180 - x - y

Ujemanje tretjega:

180 - x - y = x - y + 20

Prehod neznanke na levo stran kot vedno:

-x - y - x + y = 20 - 180

"Y" je preklican in ostaja:

-2x = - 160

x = 80 °

Druga enačba je vrednost z:

Z = x - 35 = 80 - 35 = 45 °

In vrednost in je prvega ali tretjega:

y = 180 - x - z = 180 - 80 - 45 = 55 °

Reference

1. Baldor. 1977. Elementarna algebra. Venezuelske kulturne izdaje.
2. Inštitut Monterey. Enačbe, neenakosti in absolutna vrednost. Okreval od: montereyinstitute.org.
3. Spletni učitelj. Razvrstitev linearnih ali prvih enačb. Okrevano od: profesor inline.Cl.
4. Hoffman, J. Izbira vprašanj matematike. Zvezek 2.
5. Jiménez, r. 2008. Algebra. Dvorana Prentice.
6. Zill, d. 1984. Algebra in trigonometrija. McGraw Hill.