Splošna enačba črte, katere naklon je enak 2/3

Splošna enačba črte L je naslednja: ax+by+c = 0, kjer sta a, b in c konstantna, x je neodvisna spremenljivka E in odvisna spremenljivka.

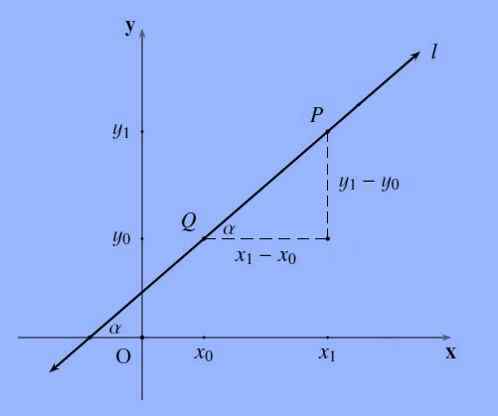
Naklon vrstice, ki je na splošno označen s črko M, ki poteka skozi točke p = (x1, y1) in q = (x0, y0) je naslednji količnik m: = (y1-y0)/(x1 -X0).

Naklon ravne črte predstavlja naklon; Bolj formalno rečeno, naklon črte je tangenta kota, ki ga ta oblika z osi x.

Treba je opozoriti, da je vrstni red, v katerem so imenovane točke, ravnodušen, saj (y0-y1)/(x0-x1) =-(y1-y0)/(-(x1-x0)) = (y1-y0) /(X1-x0).

Nerešena vrstica

Če sta znani dve točki, skozi katero prehaja črta, je enostavno izračunati njegov naklon. Toda kaj se zgodi, če te točke niso znane?

Glede na splošno enačbo linije AX+By+C = 0, mora.

Kakšna je splošna enačba črte, katere naklon je 2/3?

Ker je naklon črte 2/3, se vzpostavi enakost -a/b = 2/3, kar lahko vidi, da sta a = -2 in b = 3. Tako da je splošna enačba črte z naklonom, enaka 2/3, -2x+3y+c = 0.

Pojasniti je treba, da če ste izbrani A = 2 in B = -3, bomo dobili isto enačbo. Dejansko je 2x -3y+c = 0, kar je enako prejšnji, pomnoženo z -1. Znak C ni pomemben, saj je splošna konstanta.

Druga opažanja, ki jo je mogoče izvesti, je, da za A = -4 in B = 6 dobimo isto črto, čeprav je njegova splošna enačba drugačna. V tem primeru je splošna enačba -4x+6y+c = 0.

Obstajajo tudi drugi načini, kako najti splošno enačbo vrstice?

Odgovor je pritrdilen. Če je naklon črte znano, obstajata dve obliki, še dodatni do prejšnjega, da bi našli splošno enačbo.

Za to se uporabljata enačba točkovne in rezalne enačbe.

-Točkovna enačba: Če je m naklon črte in p = (x0, y0), točka, kjer prehaja, se enačba y-y0 = m (x-x0) imenuje točkovna enačba.

-Rezasto enačba: Če je m naklon črte in (0, b) je rez črte z osi y, potem se enačba y = mx+b imenuje rezalna enačba enačba.

Z uporabo prvega primera je pridobljeno, da je točkovna enačba črte, katere naklon je 2/3, podan z izrazom y-y0 = (2/3) (x-x0).

Če želite doseči splošno enačbo, se vsi izrazi pomnožijo s 3 na obeh straneh in so združeni skupaj, s čimer dobimo, da -2x+3y+(2 × 0-3y0) = 0 je splošna enačba črte, kjer je c = 2 × 0-3y0.

Če se uporablja drugi primer, je pridobljeno, da je vrhunska enačba črte, katere naklon je 2/3, y = (2/3) x+b.

Ponovno pomnožimo 3 na obeh straneh in razvrščamo vse spremenljivke, dobimo -2x+3y -3b = 0. Slednje je splošna enačba črte, kjer je c = -3b.

Pravzaprav, če pogledamo oba primera, je razvidno, da je drugi primer preprosto poseben primer prvega (ko x0 = 0).