Domena in kontraminij funkcije (s primeri)

Koncepti domena in protislovje funkcije Običajno jih poučujejo na tečajih za izračun, ki jih poučujejo na začetku univerzitetne kariere.

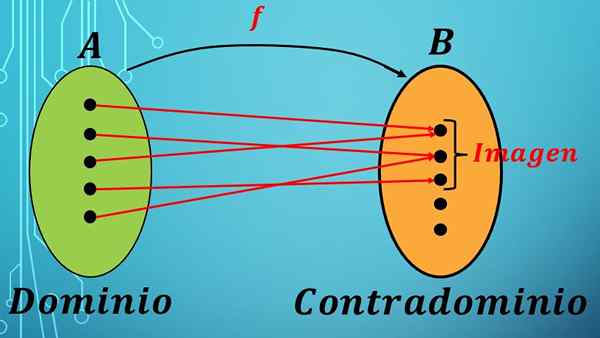
Preden določite domeno in protislovje, bi morali vedeti, kaj je funkcija. Funkcija F je dopisni zakon (pravilo) med elementi dveh nizov.

Celotno, od katerih so izbrani elementi, se imenuje domena funkcije, nabor, na katero se ti elementi pošiljajo prek F.

V matematiki je funkcija z domeno A in Contraminium B označena z izrazom F: A → B.

Prejšnji izraz pravi, da se elementi nastavitve A pošljejo na nastavitev B po dopisovanju zakona F.

Funkcija dodeli vsak element nastavka enemu elementu nabora B.

Domena in protislovje

Glede na resnično funkcijo resnične spremenljivke F (x) mora biti domena funkcije vse tiste realne številke, tako da je rezultat, ko je ocenjen v F, resnično število.

Na splošno je protislovje funkcije nabor resničnih N številk. Protislovje se imenuje tudi prihod ali nabor kodominija funkcije F.

Protislovje funkcije je vedno r?

Ne. Dokler funkcije ne preučujemo podrobno, se nabor resničnih N številk običajno jemlje kot protislovje.

Ko pa je funkcija preučena, lahko ustreznejši nabor jemljemo kot kontraminij, ki bo podmnožica R.

Ustrezen niz, omenjen v prejšnjem odstavku, sovpada s sliko funkcije.

Opredelitev slike ali razpona funkcije F se nanaša na vse vrednosti, ki izhajajo iz ocenjevanja elementa domene v F.

Primeri domene in protislovja

V naslednjih primerih je izračunati domeno funkcije in njegovo sliko je prikazano.

Primer 1

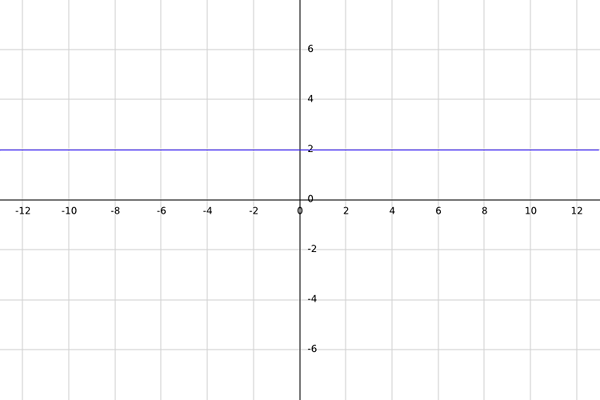
Naj bo F resnična funkcija, ki jo definira F (x) = 2.

M -domena F je vse realne številke, tako da je pri ocenjevanju v F rezultat resnično število. Protislovje zaenkrat je enako R.

Ker je dana funkcija konstantna (vedno enaka 2), mora ne glede na to, kakšno resnično je izbrano, saj bo pri ocenjevanju v F rezultat vedno enak 2, kar je resnično število.

Zato je domena dane funkcije vse realne številke; to je a = r.

Zdaj, ko je že znano, da je rezultat funkcije vedno enak 2, je slika funkcije samo številka 2, zato je mogoče protislovje funkcije na novo definirati kot b = img (f) = 2.

Zato f: r → 2.

Primer 2

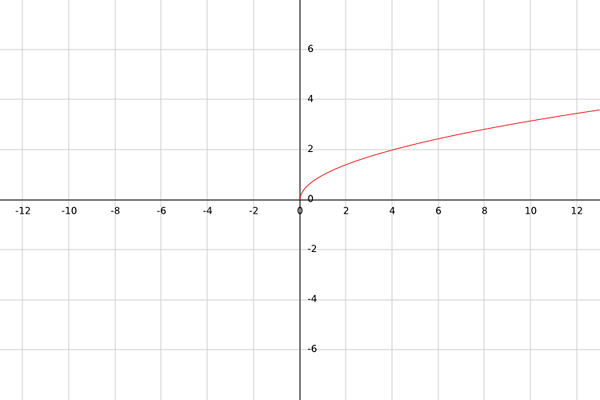
Naj bo g resnična funkcija, ki jo definira g (x) = √x.

Dokler podoba G ni znana, je kontraminij G B = r.

S to funkcijo je treba upoštevati, da so kvadratne korenine opredeljene samo za ne -negativne številke; to je za številke, večje ali enake kot nič. Na primer, √-1 ni resnično število.

Zato mora biti mojstrstvo funkcije G vse številke, večje ali enake kot nič; to je x ≥ 0.

Zato je a = [0,+∞).

Za izračun območja je treba opozoriti, da bo vsak rezultat g (x), ker je kvadratni koren, vedno večji ali enak ali enak. To je b = [0,+∞).

Za zaključek, G: [0,+∞) → [0,+∞).

Primer 3

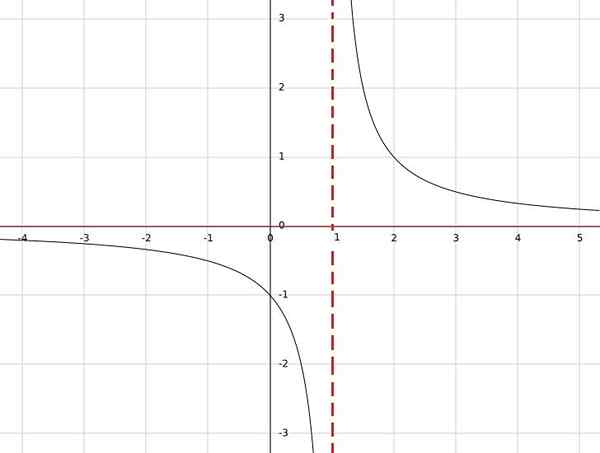
Če imate funkcijo H (x) = 1/(x-1), ta funkcija ni definirana za x = 1.

Po drugi strani bo rezultat za katero koli drugo resnično vrednost resnično število. Zato so domena vse reaise, razen ene; to je a = r \ 1.

Na enak način je razvidno, da je edina vrednost, ki je ni mogoče dobiti kot rezultat, 0, saj mora biti delež enak nič.

Zato je slika funkcije niz vseh reaisov, razen nič, potem jemljemo kot kontraminij b = r 0.

Za zaključek, h: r \ 1 → r \ 0.

Opazovanja

Domena in slika nista enaka, kot je prikazano v primerih 1 in 3.

Ko je funkcija graf na kartezijanski ravnini, je domena predstavljena z osjo x in protitrthiominium ali območje predstavlja os y.