Eksponentna porazdelitev

Pojasnjujemo, kaj je eksponentna porazdelitev, njegove značilnosti, formule, primere in postavljene rešene vaje

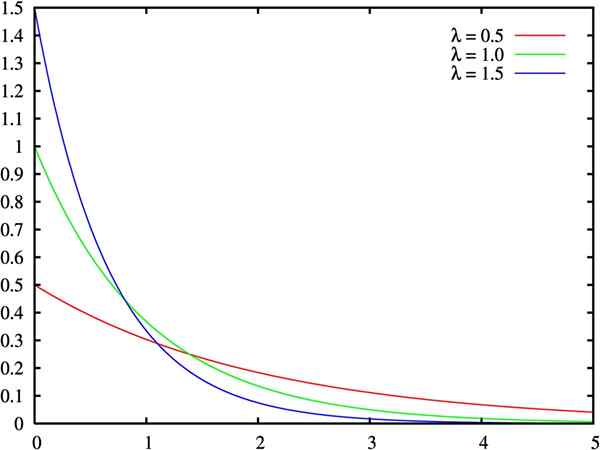
Graf funkcije gostote eksponentne porazdelitve za tri vrednosti parametra Lambda. Vir: Wikimedia Commons.

Kaj je eksponentna porazdelitev?

The eksponentna porazdelitev Gre za verjetnostni model za neprekinjene naključne spremenljivke. To pomeni, da lahko s tem poznate verjetnost pojavljanja določene vrednosti spremenljivke, tako da gre za porazdelitev verjetnosti.

Za pridobitev distribucije se začne od Funkcija gostote, ki ima eksponentno obliko parametra λ> 0:

Funkcija gostote kot take ne omogoča izračuna verjetnosti, toda ko je vzpostavljena f (x), se porazdelitvena funkcija f (x), s katero se verjetno dobijo, dobimo z integracijo f (x). Na primer, verjetnost p, da naključna spremenljivka ima vrednosti med 0 in x, je:

Izvajanje integracije, ki je zelo preprosta, saj je integral eksponenta enak eksponentni, razen konstant, ki spremljajo argument, je pridobljeno:

Eksponentna porazdelitev se pogosto uporablja za določitev verjetnosti dogodka po določeni čakalnici, na primer čas, ki se zgodi v pojavu bolnišnice, preden pacient pride.

Pogosto se dogodki nanašajo na okvaro ali razčlenitev električnih, elektronskih in drugih vrst. V tem primeru eksponentna porazdelitev pomaga oceniti čas, ki je potreben, da komponenta ne uspe, in tudi čas med popravili. To je znano kot teorija zanesljivosti.

Značilnosti eksponentne porazdelitve

Nekatere najbolj izjemne značilnosti funkcije gostote f (x) eksponentne porazdelitve so naslednje:

• f (x) je pozitiven.
• Območje pod krivuljo y = f (x) = λe^−λx Vedno je enak 1, ker mora biti vsota verjetnosti pojava vseh vrednosti spremenljivke 1. To je pogoj, ki ga izpolnjujejo funkcije gostote. To območje se izračuna prek integrala:

Vam lahko služi: anuma

Pomanjkanje eksponentnega distribucijskega pomnilnika

Najbolj izjemna značilnost eksponentne distribucije je pomanjkanje pomnilnika. Na primer, predpostavimo, da se pretečeni čas modelira s to porazdelitvijo, dokler ne pride do neuspeha elementa.

No, pomanjkanje pomnilnika se nanaša na vedeti, da je element deloval za čas preživetja "S", ne spreminja verjetnosti, da bo element še naprej potekal do določenega dodatnega časa "t".

Se pravi, verjetnost, da element ne uspe od tu do določenega časa (na primer 1 minuta, 1 ura), ni odvisna od tega, da je do zdaj dobro deloval.

Matematično se izračuna po definiciji verjetnosti neodvisnih dogodkov:

Zato verjetnost ni odvisna od časa ali časa preživetja.

Formule

1.- Funkcija gostote eksponentne porazdelitve je:

Kjer je λ parameter porazdelitve.

2.- Kot je opisano zgoraj, je porazdelitev verjetnosti označena kot F (x), različne verjetnosti pa dobimo z integracijo funkcije gostote:

3.- Iz zgornjega izhaja, da je verjetnost, da spremenljivka vzame vrednosti manj kot ali enake "x", p [x≤x] = 1 − e^−λx.

4.- Območje pod krivuljo y = f (x), vključeno med A in B, omogoča izračun verjetnosti, da je spremenljivka v intervalu [A, B]. To območje je:

P [a ≤ x ≤ b] = f (b) - f (a)

5.- Vrednost p [x ≥ a] je 1 - f (a) = 1 - (1 - e^−λx) = e^−λx

Pričakovana vrednost eksponentne porazdelitve

Upanje ali pričakovana vrednost e (x) eksponentne porazdelitve je vrednost, ki se pričakuje pogosteje. Izračuna se iz integrala:

Vam lahko služi: tehnike registracije informacij

Ki jo zlahka reši metoda integracije po delih. Rezultat je:

E (x) = 1/λ

Odstopanje eksponentne porazdelitve

Za izračun variance je treba določiti integral:

Ki se rešuje tudi z metodo integracije po delih, da dobimo:

Var (x) = 1/λ²

Posebnost eksponentne porazdelitve je, da je standardni odklon S (x), opredeljen kot kvadratni koren variance,:

S (x) = √Var (x) = √ (1/λ²) = 1/λ

To pomeni, da je standardni odklon enak upanju na distribucijo.

Primeri eksponentne porazdelitve

Podatki vzorcev ogljika 14

Eksponentna porazdelitev se uporablja za določitev časa, ki je potreben za razpadanje radioaktivnih delcev. Ti časi se do danes uporabljajo fosilni vzorci z radiokarbonom.

Čas je potreben za preverjanje pošte

Lahko modelirate čas, ki ga uporabniki sprejmejo za pregled svojega e -poštnega sporočila, ko je obvestilo prejeto, z eksponentno distribucijo. Recimo, da je parameter porazdelitve λ = 0.2 torej verjetnost, da si človek vzame manj kot 1 minuto, da pregleda svoje e -poštno sporočilo, je:

Ta integral je bil razrešen na začetku, le še vedno je nadomestiti številčne vrednosti v raztopini in izračunati končni rezultat:

P [x ≤ 1] = 1 -^-0.2×1 = 1− e^-0.2 = 1– 0.819 = 0.181

Prav tako ga lahko neposredno zamenjate s funkcijo f (x), ki je navedena zgoraj, da dobite f (1).

Vaje

Vaja 1

Poiščite verjetnost, da bo oseba pozneje eno uro pregledala njihovo e -pošto, če je porazdelitev verjetnosti eksponentna, s parametrom λ = 0.2.

Rešitev

P [x ≥ 60] je treba izračunati, saj je 1 ura enakovredna 60 minutam in verjetnost, da se oseba pozno 60 minut ali več za preverjanje pošte zahteva. Verjetnost se izračuna z istim integralom, predstavljenim na začetku, samo spreminja meje integracije:

Lahko vam služi: Rapa Nui: Zgodovina, značilnosti, kultura, tradicije

Pridobljena vrednost je majhna, zato je zelo malo verjetno, da si človek vzame več kot eno uro za pregled e -pošte.

Vaja 2

Električne žarnice imajo običajno končno trajanje, razen znamenite žarnice gasilske postaje v Livermoreju v Kaliforniji, ki od prvega leta 1901 nikoli ni uspela.

Predpostavimo, da trajanje trenutne žarnice sledi eksponentni porazdelitvi s pričakovano vrednostjo 8 mesecev. Izračunati:

a) Kakšna je verjetnost, da bo žarnica trajala med 5 in 14 meseci?

b) verjetnost, da bo žarnica trajala več kot 25 mesecev, vedoč, da ima več kot 11 mesecev v delovanju.

Rešitev

Prva stvar je najti vrednost λ s pričakovano vrednostjo porazdelitve e (x) = 8 mesecev. Glede na to, kar je bilo rečeno v prejšnjem razdelku, je pričakovana vrednost obratna parametra λ:

E (x) = 1 /λ → λ = 1 /e (x) = 1/8 = 0.125

Nato se zahtevana verjetnost izračuna s pomočjo integrala, ki je podana na začetku, vendar priročno spreminja meje integracije:

Nato ga nadomestimo v funkciji F (X), podani v prejšnjem razdelku, kot sledi:

P [5 ≤ x ≤ 14] = f (14) - f (5) = [1 - e^{-(0.125 × 14)}] - [1 - e^{-(0.125 × 5)}] = 0.36

Rešitev b

Za odgovor na to vprašanje bo uporabljena lastnost pomanjkanja pomnilnika, zgoraj navedena. Kot je znano, da traja že več kot 11 mesecev, potem:

S = 11 mesecev

Dodatni čas za traja 25 mesecev ali več je:

T = 14 mesecev

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14│t ≥ 11] = e^{–0.125 × 14} = 0.174