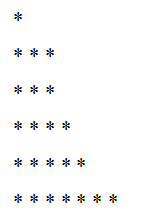Aditivna razgradnja

The aditivna razgradnja pozitivnega števila je izraziti kot vsoto dveh ali več pozitivnih številk. Tako lahko to številka 5 izrazi kot 5 = 1+4, 5 = 2+3 ali 5 = 1+2+2. Vsak od teh načinov pisanja številke 5 je tisto, čemur bomo rekli aditivni razgradnji.

Če smo pozorni, lahko vidimo, da izrazi 5 = 2+3 in 5 = 3+2 predstavljajo isto sestavo; Oba imata enake številke. Vendar pa se običajno zapiše le za tolažbo, ki je po merilih od najmanjših do največjega.

Aditivna razgradnja

Kot še en primer lahko vzamemo številko 27, ki jo lahko izrazimo kot:

27 = 7+10+10

27 = 9+9+9

27 = 3+6+9+9

27 = 9+18

Aditivno razgradnjo je zelo koristno orodje, ki nam omogoča okrepitev znanja o oštevilčevih sistemih.

Kanonična razgradnja aditiva

Ko imamo število več kot dveh številk, je določena oblika razpadanja v večkratnikih 10, 100, 1000, 10.000 itd., ki nadoknadijo. Ta način pisanja poljubne številke se imenuje kanonični aditivni razpad. Na primer, številka 1456 ga lahko razgradi na naslednji način:

1456 = 1000 + 400+ 50 + 6

Če imamo številko 20 846 295, bo vaša kanonična razgradnja aditiva:

20 846 295 = 20 000 000 + 800 000 + 40 000 + 6000 + 200 + 90 +5.

Zahvaljujoč tej razgradnji lahko vidimo, da vrednost določene številke daje položaj, ki ga zaseda. Vzemimo kot primer številke 24 in 42:

24 = 20 + 4

42 = 40 +2

Tu lahko vidimo, da ima v 24 vrednosti 20 enot, na 4 pa vrednost 4 enot; Po drugi strani ima 42 40 40 enot in 2 od dveh enot. Čeprav obe številki uporabljata iste številke, so njihove vrednosti popolnoma drugačne glede na položaj, ki ga zasedajo.

Vam lahko služi: x kvadrat

Prijave

Ena od aplikacij, ki jih lahko damo za razgradnjo aditivov, je v nekaterih vrstah demonstracij, v katerih je zelo koristno videti pozitivno celo število kot vsoto drugih.

Primer teorema

Vzemimo kot primer naslednji izrek z njihovimi demonstracijami.

- Biti z celo število 4 števk, potem je Z deljen za 5, če je njegova številka, ki ustreza enotam, nič ali pet.

Demonstracija

Spomnimo se, kaj je delitev. Če imamo "A" in "B" cele številke, rečemo, da "A" deli "B", če obstaja celo število "C", tako da je B = A*C.

Ena od lastnosti delitve nam pove, da če sta "A" in "B" deljiva med "C", potem je odštevanje "A-B" tudi.

Biti z celo število 4 števk; Zato lahko pišemo z z in z = ABCD.

Z uporabo kanoničnega aditivnega razgradnje moramo:

Z = a*1000 + b*100 + c*10 + d

Jasno je, da je*1000 + B*100 + C*10 deljiv med 5. Zato imamo, da je z deljen med 5, če je z - (a*1000 + b*100 + c*10) deljen med 5.

Toda z - (a*1000 + b*100 + c*10) = d in d je ena sama številka številke, zato je edini način, da je med 5 deljiv, da je 0 ali 5.

Zato je z deljen med 5, če je d = 0 ali d = 5.

Upoštevajte, da če ima z N števke, je demonstracija popolnoma enaka, le spremembe, ki bi jih zdaj napisali z = a₁Do₂… Do_n In cilj bi bil to dokazati_n je nič ali pet.

Particije

Pravimo, da je particija pozitivnega števila način, kako lahko napišemo številko kot vsota pozitivnih celih števil.

Vam lahko služi: konvergenčni radio: definicija, primeri in vaje rešene

Razlika med aditivnim razpadom in predelnico je v tem, da je v prvi iskani, da jo je mogoče vsaj razčleniti na dva ali več, v particiji to omejitev.

Tako imamo naslednje:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+2+2

Zgoraj so particije 5.

Se pravi, da je vsa aditivna razgradnja particija, vendar ni vsa particija nujno aditivna razgradnja.

V teoriji številk temeljni teorem aritmetike zagotavlja, da je mogoče vsako celotno število napisati edinstveno kot produkt bratrancev.

Ko preučimo particije, je cilj določiti, na koliko načinov je mogoče zapisati pozitivno celo število kot vsoto drugih celih števil. Zato definiramo funkcijo particije, kot je predstavljena spodaj.

Opredelitev

Funkcija particije p (n) je opredeljena kot število načinov, kako lahko pozitivno celo n zapišemo kot vsota pozitivnih celih števil.

Če se vrnemo na primer 5, moramo:

5 = 5

5 = 1+4

5 = 2+3

5 = 1+1+3

5 = 1+2+2

5 = 1+1+1+2

5 = 1+1+1+1+1

Na ta način je p (5) = 7.

Grafi

Tako particije kot tudi aditivne razgradnje števila n je mogoče geometrijsko predstaviti.  Recimo, da imamo aditivno razgradnjo n. V tej razgradnji lahko dodatke popravite tako, da se člani vsote naročijo od najmanj do največjega. Torej, vredno je:

n = a₁ + do₂ + do₃ +… + A_r z

do₁ ≤ a₂ ≤ a₃ ≤ ... ≤ a_r.

Lahko razgradnje izgradimo na naslednji način: v prvi vrsti označimo a₁-točke, nato v nadaljevanju označujemo₂-točke in tako naprej, dokler ne dosežete_r.

Vam lahko služi: neenakost trikotnika: demonstracija, primeri, rešene vaje

Vzemimo kot primer številka 23 in njegovo naslednjo razgradnjo:

23 = 5 + 4 + 7 + 3 + 1 +3

Naročimo to razgradnjo in imamo:

23 = 1 + 3 + 3 + 4+ 5 + 7

Njegov ustrezni graf bi bil:

Prav tako, če ta graf preberemo navpično namesto vodoravno, lahko dobimo razgradnjo, ki se morda razlikuje od prejšnjega. V primeru 23 izstopa naslednje:

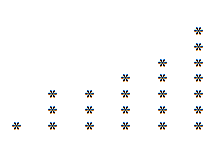
Torej imamo, da jih 23 napišemo tudi kot:

23 = 6 + 5 + 5 + 3 + 2 + 1 + 1.