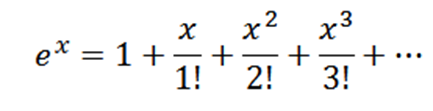Zaporedni derivati

Kaj so zaporedni derivati?

The zaporedni derivati So tisti, ki izhajajo iz funkcije po drugem derivatu. Postopek za izračun zaporednih derivatov je naslednji: Obstaja funkcija F, ki jo lahko izpeljemo in pridobimo izpeljano funkcijo f '. Temu izpeljavemu izpeljave F lahko ponovno izpeljemo in pridobimo (f ')'.

Ta nova funkcija se imenuje druga derivat; Vsi derivati, izračunani iz drugega, so zaporedni; Te, imenovane tudi višje vrstni red, imajo velike aplikacije, kot so dajanje informacij o poteku grafa funkcije, test drugega izpeljanka za relativne konce in določitev neskončnih serij.

Opredelitev

Z uporabo Leibniz zapisa imamo, da je izpeljanka funkcije "y" glede na "x" dy/dx. Da bi izrazili drugi izpeljan "y" z uporabo notacije Leibniz, pišemo na naslednji način:

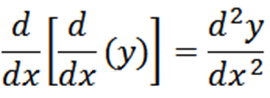
Na splošno lahko zaporedne derivate izrazimo na naslednji način z zapisom Leibniz, kjer n predstavlja vrstni red izpeljane.

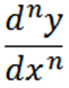
Drugi uporabljeni zapisi so naslednji:

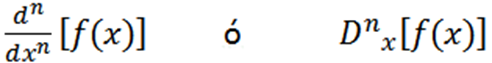
Nekaj ​​primerov, kjer lahko vidimo različne zapise, je:

Primer 1

Pridobite vse derivate funkcije F, opredeljene z:

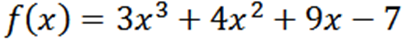
Z uporabo običajnih tehnik napotitve imamo, da je F:

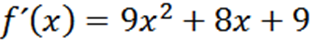
Ponavljanje postopka lahko dobimo drugi izpeljan, tretji izpeljan in tako naprej.

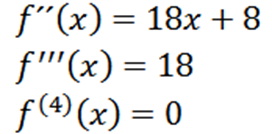
Upoštevajte, da je četrti izpeljan nič, ničelni derivat pa je nič, zato moramo:

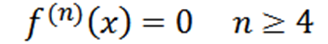
Primer 2

Izračunajte četrto, pridobljeno iz naslednje funkcije:

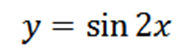
Izvedba dane funkcije, ki jo imamo kot rezultat:

Hitrost in pospešek

Ena od motivacij, ki je privedla do odkritja derivata, je bilo iskanje definicije takojšnje hitrosti. Uradna definicija je naslednja:

Vam lahko služi: Primo številke: značilnosti, primeri, vaje

Naj y = f (t) funkcija, katere graf v trenutku opisuje smer delca t, Potem je njegova hitrost v trenutku t dana:

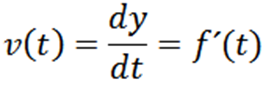
Ko dobimo hitrost delca, lahko izračunamo takojšen pospešek, ki je opredeljen na naslednji način:

Trenutni pospešek delca, katerega usmeritev je podana z y = f (t) je:

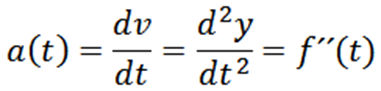
Primer 1

Delec se premika na črti glede na funkcijo položaja:

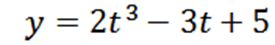
Kjer se "y" meri v metrih in "t" v nekaj sekundah.

• V kakšnem trenutku je vaša hitrost 0?
• V tem trenutku je njegov pospešek 0?

Z izpeljavo funkcije položaja "y" imamo, da njeno hitrost in pospeševanje daje:

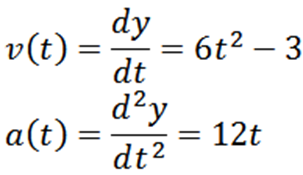
Da bi odgovorili na prvo vprašanje, je dovolj, da ugotovimo, kdaj je funkcija V nič; to je:

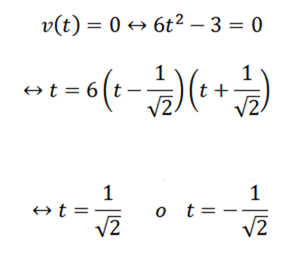
Nadaljemo z naslednjim vprašanjem Analogno:

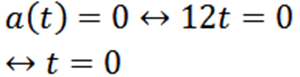
Primer 2

Delci se premika po črti v skladu z naslednjo enačbo gibanja:

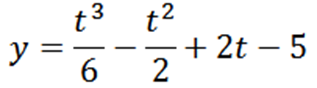
Določite "t, y" in "v", ko je a = 0.

Vedoč, da hitrost in pospeševanje daje

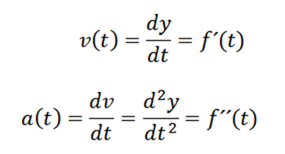
Nadaljujemo z izpeljavo in pridobivanje:

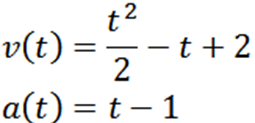
Delamo a = 0, imamo:

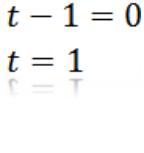
Kjer lahko sklepamo, da je vrednost T, tako da je A enaka nič, t = 1.

Nato moramo v T = 1 funkcijo položaja in funkcije:

Prijave

Izpeljava mplícita

Zaporedne derivate lahko dobimo tudi z implicitno izpeljavo.

Primer

Glede na naslednjo elipse poiščite "y":

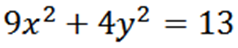
Implicitno izpeljamo glede na X, imamo:

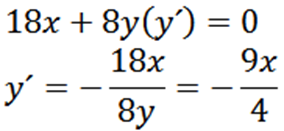
Nato nam daje implicitno, da se implicitno denira v zvezi z X:

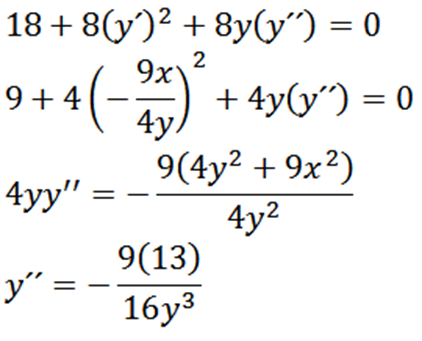
Končno imamo:

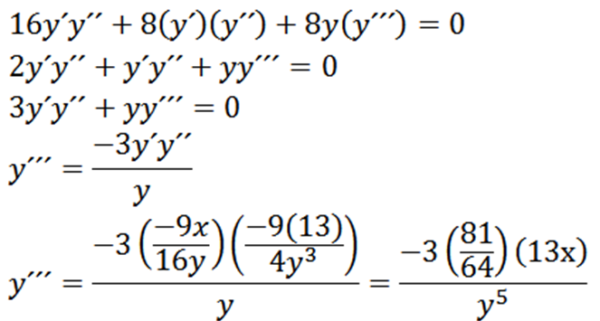
Relativne skrajnosti

Druga uporaba, ki jo lahko damo v derivati ​​drugega reda, je v izračunu relativnih koncev funkcije.

Vam lahko služi: koliko osi simetrije ima krog?

Merila prvega izpeljanka za lokalne skrajnosti nam pravijo, da če imamo v intervalu neprekinjeno funkcijo F (a, b) in je C, ki pripada omenjenemu intervalu je kritična točka), lahko pride do enega od teh treh primerov:

• Če je f '(x)> 0 za kateri koli x, ki pripada (a, c) in f' (x)<0 para x perteneciente a (c,b), entonces f(c) es un máximo local.
• Če je f '(x) 0 za x, ki pripada (c, b), potem je f (c) lokalni minimum.
• Če ima f '(x) enako prijavo v (a, c) in v (c, b), to pomeni, da F (c) ni lokalni konec.

Z uporabo kriterijev drugega izvedenega finančnega instrumenta lahko vemo, ali je kritično število funkcije največji ali lokalni minimum, ne da bi bilo treba storiti, kar je znak funkcije v prej omenjenih intervalih.

Kriterij drugega premika nam pove, da če je f '(c) = 0 in da je f "(x) neprekinjen v (a, b), se zgodi, če je f" (c)> 0, potem je f (c) a a a Lokalni minimum in če f "(c) < 0 entonces f(c) es un máximo local.

Če f "(c) = 0, ne moremo ničesar sklepati.

Primer

Glede na funkcijo f (x) = x⁴ + (4/3) x³ - 4x², Poiščite največji in najmanjši sorodnik F Uporaba meril drugega izpeljanka.

Najprej izračunamo f '(x) in f "(x) in imamo:

f '(x) = 4x³ + 4x² - 8x

f "(x) = 12x² + 8x - 8

Zdaj, f '(x) = 0 da, in samo, če je 4x (x + 2) (x - 1) = 0, in to se zgodi, ko x = 0, x = 1 ali x = - 2.

Da bi ugotovili, ali so pridobljene kritične številke relativne skrajnosti, samo ocenijo v F "in tako upoštevajte njegov znak.

Vam lahko služi: Heptagon

f "(0) = - 8, torej f (0) je lokalni maksimum.

f "(1) = 12, tako da je f (1) lokalni minimum.

f "(- 2) = 24, torej f (- 2) je lokalni minimum.

Serija Taylor

Biti f funkcija, opredeljena na naslednji način:

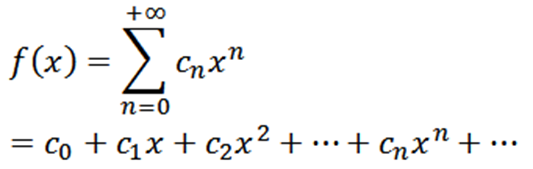
Ta funkcija ima polmer konvergence r> 0 in izhaja iz vseh naročil v (-r, r). Naslednji derivati ​​F nam dajo:

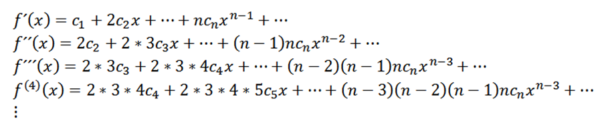
Jemljemo x = 0, lahko dobimo vrednosti c_n Odvisno od njegovih derivatov na naslednji način:

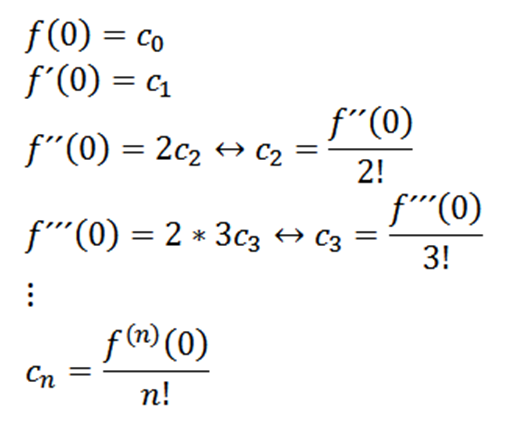
Če vzamemo n = 0 kot funkcijo f (tj. F^0 = f), lahko funkcijo prepišemo na naslednji način:

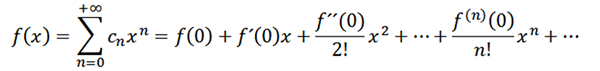
Zdaj pa upoštevajte funkcijo kot niz moči pri x = a:

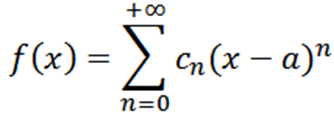
Če izvedemo analizo, analogno prejšnji, bi morali funkcijo f napisati kot:

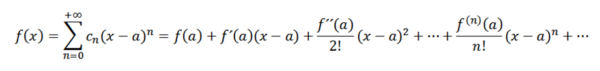
Te serije so znane kot Taylor F v seriji. Ko je A = 0, imamo določen primer, imenovan Maclaurin Series. Ta vrsta serij je velikega matematičnega pomena, zlasti pri številčni analizi, saj lahko po zaslugi teh določimo funkcije v računalnikih, kot je E^x , greh (x) in cos (x).

Primer

Pridobite serijo Maclaurin za E^x.

Upoštevajte, da če f (x) = e^x, potem f^(N)(x) = e^x in f^(N)(0) = 1, tako da je vaša serija Maclaurin: