Domača stran
Matematika
Redni, nepravilen dekagon, lastnosti, primeri

Matematika

Redni, nepravilen dekagon, lastnosti, primeri

On decagon Gre za ravno figuro z poligonom z 10 strani in 10 točki ali nasvetov. Dekagoni so lahko redni ali nepravilni, v prvem primeru imajo vse strani in notranji koti enak ukrep, v drugem pa se strani in/ali koti med seboj razlikujejo.

Slika 1 prikazuje primere dekagonov vsake vrste in kot vidimo, je navadni dekagon zelo simetričen.

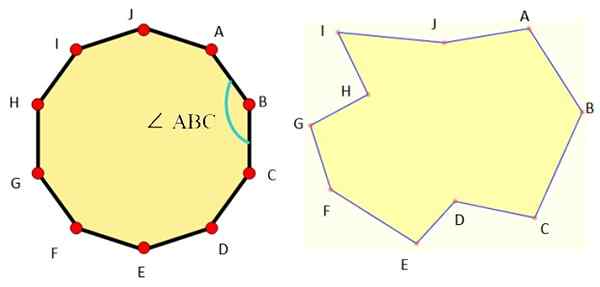Slika 1. Na levi redni dekagon in na desni nepravilen dekagon. Vir: Wikimedia Commons/F. Zapata/Mathpenref.

Osnovni elementi vsega Decagona so:

-Strani, linijski segmenti, ki se pri pridružitvi Decagonu.

-Točke ali točke med vsako zaporedno stranjo.

-Notranji in zunanji koti med sosednjimi stranmi.

-Diagonale, segmenti, ki združujejo dve nesorazmerni točki.

Vrtice se imenujejo z velikimi črkami, kot je prikazano na sliki 1, kjer so bile uporabljene prve črke abecede, vendar je mogoče uporabiti katero koli črko.

Strani so simbolizirane z dvema črkama tokov, med katerimi sta na primer AB stran tista med točkama A in B. Na enak način je to storjeno z diagonali, tako da imamo diagonalno AF, ki se pridruži točkam A in F.

Za kote uporabljamo ta simbol: ∠, podobno kot nagnjen L. Na primer, kot ∠ ABC je tisti, katerega točka je B in katerih strani so segmenti AB in BC.

[TOC]

Redni dekagon

V rednem dekagonu imajo vse strani enak ukrep, pa tudi notranje kote. Zato naj bi bilo enakostranično (enake strani) in Enako (Enaki koti). Je zelo simetrična figura

Notranji koti navadnega dekagona

Če želite najti mero notranjega kota navadnega poligona, vključno z običajnim dekagonom, se uporablja naslednja formula:

$I=\frac(n-2)\times 180^^on$

Kje:

-I je merilo kota v stopinjah.

-n je število strani poligona. V primeru Decagona n = 10.

Vam lahko služi: Heptagon

Zamenjava n = 10 V prejšnji formuli dobimo naslednje:

$I=\frac(10-2)\times 180^^o10=144^^o$

Zdaj je rečeno, da je poligon konveksna Če so njegovi kotni ukrepi manjši od 180 °, sicer je poligon konkavno. Kot vsak notranji kot običajnega dekagona meri 144 ° in je manjši od 180 °, potem je tudi konveksni poligon.

Vsota notranjih kotov

Vsota ukrepov notranjih kotov katerega koli poligona je v stopinjah:

S = (n-2) x 180 °; n je vedno večji od 2

V tej formuli moramo:

-S je vsota ukrepov notranjih kotov.

-n je število strani. Za dekagon n = 10

Uporaba formule za n = 10 rezultatov:

S = (10 - 2) x 180 ° = 1440 °

Zunanji koti

Zunanji kot je oblikovan med eno stranjo in razširitvijo sosednje strani, poglejmo:

Slika 2.- Zunanji kot običajnega dekagona meri 36 °. Fontana. Wikimedia commons/f. Zapata.

Kot ∠ ABC plus zunanji kot doda 180 °, to je Dopolnilno. Zato je zunanji kot enak 180 ° 144 ° = 36 °, kot vidimo na sliki.

Število diagonalov

Kot je bilo že omenjeno. Koliko diagonalov lahko izsledimo v dekagonu? Ko je število vrhov majhno, jih je mogoče enostavno prešteti, ko pa se ta številka poveča, lahko izgubite račun.

Na srečo obstaja formula, ki ve, koliko diagonalov, ki jih ima poligon n strani:

$D=\fracn(n-3)2$

Za Decagon nadomestimo n = 10 in dobimo:

D = 10 x (10 - 3) /2 = 35

V običajnem dekagonu so vse diagonale rezane v eni točki, kar je središče slike:

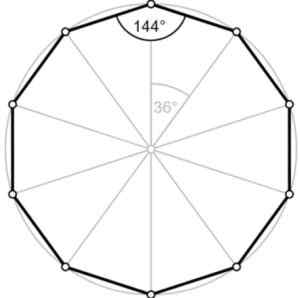Slika 3. Koti in diagonale rednega dekagona. Vir: Wikimedia Commons.

Center

Središče poligona je opredeljeno kot tista enača oddaljena točka katerega koli vrha. Na prejšnji sliki središče sovpada s točko presečišča vseh diagonalov.

Obseg

Če ima redni dekagon stran A, je njegov obod P vsota vseh strani:

Vam lahko služi: 90 delitev: kaj so in razlaga

P = 10.do

Območje

Poznavanje dolžine do Na strani je redno območje dekagona izračunano z:

$A=\left (\frac52 \right )cot\left ( \frac\pi 10 \right )a^2$

Približna formula za območje je:

$A=\frac10a^24 \times tg\left ( \frac\pi 10 \right )\simeq 7.694a^2$

In tretja možnost za iskanje območja je dolžina apotema l_Do. To je segment, ki se pridruži sredi točke na eni strani s sredino poligona.

V tem primeru lahko območje izračunamo po formuli:

$A=\fracP.L__A2=\frac10a\times L_A2$

Nepravilen dekagon

Nepravilni dekagon ni enakostraničen ali enakomeren, na splošno pa nima simetrije redne figure, čeprav imajo nekateri dekagoni lahko os simetrije.

Lahko so tudi konveksni ali konkavni, če obstajajo notranji koti, večji od 180 °.

Nepravilni dekagon slike 1 je konkaven, saj so nekateri njegovi notranji koti večji od 180 °. Očitno je, da obstaja veliko kombinacij kotov in strani, ki povzročajo nepravilen dekagon.

V vsakem primeru je izpolnjeno:

-Notranji koti nepravilnega dekagona dodajo tudi 1440 °.

-Ima tudi 35 diagonalov.

Območje nepravilnega dekagona Gaussovih determinantov

Na splošno ni edinstvene formule za iskanje območja nepravilnega poligona, saj so stranice in koti različni. Vendar lahko najdete spoznanje koordinat vrhov in izračunavanje Gaussove determinante:

-Pokličimo (x_n , in_n) na koordinate tokov, z n se razlikuje od 1 do 10.

-Lahko začnete z katere koli točke, do katere bodo dodeljene koordinate (x x₁, in₁). Zdaj morate v tej formuli zamenjati vrednosti vsake koordinate:

$A=\left |\frac(x_1y_2-x_2y_1)+(x_2y_3-x_3y_2)+(x_3y_4-x_4y_3)+… (x_ny_1-x_1y_n)2 \right |$

Kjer so dejavniki natančno delovanje med oklepaji.

-Pomembno je upoštevati, da zadnji determinant vključuje prvo točko skupaj z zadnjim. Za Decagon bi bilo tako:

(x₁₀in₁ - x₁in₁₀)

Vam lahko služi: interpolacija LaGrange

Pomembno: Palice so tiste z absolutno vrednostjo in pomenijo, da je končni rezultat vedno s pozitivnim znakom.

Postopek je lahko naporen, če ima številka veliko vrhov, v primeru Decagona je 10 operacij, zato je priporočljivo narediti tabelo ali seznam.

Vaja rešena

Izračunajte nepravilno območje decagona, prikazano na sliki. Koordinate vrhov so a, b, c ... j, katerih vrednosti so prikazane na levi strani.

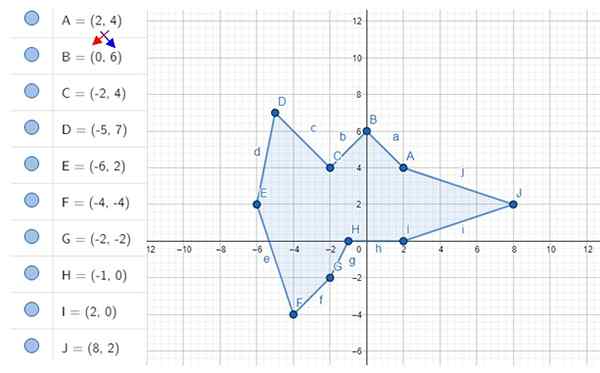Slika 4. Nepravilen decagon in njene točke. Vir: f. Zapata z geogebro.

Rešitev

-Vsako od 10 operacij:

2 × 6 - 4 × 0 = 12 - 0 = 12
0 × 4 - 6 × (-2) = 0 + 12 = 12
(-2) × 7- 4 × (-5) = -14 + 20 = 6
(-5) × 2 -7 × (-6) = -10 + 42 = 32
(-6) × (-4) -2 × (-4) = 24 + 8 = 32
(-4) × (-2)-(-4) × (-2) = 8-8 = 0
(-2) × 0-(-2) × (-1) = 0 -2
(-1) × 0 - 0 × (2) = 0 - 0 = 0
2 × 2 - 0 × 8 = 4 - 0 = 4
8 × 4 -2 × 2 = 32 - 4 = 28

-Dodamo rezultate:

12 + 12 + 6 + 32 + 32 + 0 + (-2) + 0 + 4 + 28 = 124

Pozitiven rezultat dobimo tudi brez palic absolutne vrednosti, če pa je negativen, se enako spremeni.

-Prejšnji rezultat je razdeljen z 2 in to je območje poligona:

A = 124/2 = 62

Lastnosti Decangon

Spodaj je povzetek splošnih lastnosti dekagona, bodisi redne ali nepravilne:

-Ima 10 strani in 10 vrhov.

-Vsota notranjih kotov je 1440 °.

-Obstaja 35 diagonalov.

-Obod je vsota vseh strani.

-Trikotnike lahko ustvarite znotraj segmentov risanja poligona od točke do vseh ostalih. V dekagonu je mogoče na ta način narisati 8 trikotnikov, kot je prikazano spodaj:

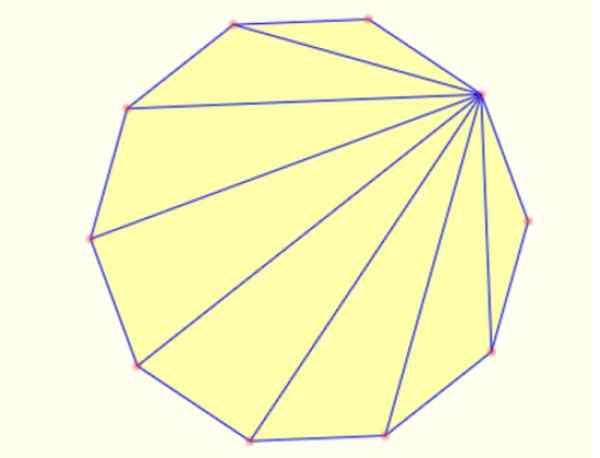Slika 5. Notranji trikotniki v običajnem dekagonu. Vir: Mathpenref.

Reference

Aleksander, d. 2013. Geometrija. 5. Izdaja. Cengage učenje.
Decagon.com. Decagon. Okreval od: Decagon.com
Open Reference Math Open. Decagon. Okreval od: Mathpenref.com.
Sangaku matematika. Elementi poligona in njegove klasifikacije. Okreval od: sangakoo.com.
Wikipedija. Decagon. Okrevano od: je.Wikipedija.com.