Koliko rešitev ima kvadratna enačba?

Kvadratna enačba ali enačba druge stopnje ima lahko nič, eno ali dve resnični rešitvi, odvisno od koeficientov, ki se pojavljajo v omenjeni enačbi. Če delate na zapletenih številkah, potem lahko rečete, da ima vsaka kvadratna enačba dve rešitvi.

Za začetek kvadratne enačbe je enačba oblike AX²+BX+C = 0, kjer so A, B in C realne številke in X je spremenljivka.

Govori se, da je x1 rešitev prejšnje kvadratne enačbe, če je pri zamenjavi x z x1 izpolnjena enačba, torej če je a (x1) ²+b (x1)+c = 0.

Če imate na primer enačbo x²-4x+4 = 0, potem je x1 = 2 rešitev, saj (2) ² (2) +4 = 4-8+4 = 0.

Nasprotno, če je x2 = 0 zamenjan, dobimo (0) ²-4 (0) +4 = 4 in kot 4 ≠ 0 potem x2 = 0 ni rešitev kvadratne enačbe.

Rešitve kvadratne enačbe

Število rešitev kvadratne enačbe je mogoče ločiti v dveh primerih, ki sta:

1.- V resničnih številkah

Pri delu z resničnimi številkami imajo lahko kvadratne enačbe:

-Zero rešitve: Se pravi, da ni resničnega števila, ki bi izpolnjevala kvadratno enačbo. Na primer, enačba dana x²+1 = 0, ni resničnega števila, ki bi izpolnjevala omenjeno enačbo, saj je oba x² večja ali enaka nič in 1 je večja kot nič, tako da bo njegova vsota večja Strogo od nič.

-Ponavljajoča rešitev: Obstaja ena sama resnična vrednost, ki izpolnjuje kvadratno enačbo. Na primer, edina rešitev enačbe x²-4x+4 = 0 je x1 = 2.

-Dve različni rešitvi: Obstajata dve vrednosti, ki izpolnjujeta kvadratno enačbo. Na primer, x²+x -2 = 0 ima dve različni rešitvi, ki sta x1 = 1 in x2 = -2.

2.- V zapletenih številkah

Pri delu s kompleksnimi številkami imajo kvadratne enačbe vedno dve rešitvi, ki sta Z1 in Z2, kjer je Z2 konjugat Z1. Poleg tega jih je mogoče razvrstiti med:

-Kompleksi: Raztopine so oblike z = p ± qi, kjer sta p in q realna številka. Ta primer ustreza prvemu primeru prejšnjega seznama.

-Čisti kompleksi: Ko je resnični del rešitve enak ničle, to pomeni, da ima rešitev obliko z = ± qi, kjer je Q resnično število. Ta primer ustreza prvemu primeru prejšnjega seznama.

-Kompleksi z namišljenim delom enaki nič: Ko je kompleksni del raztopine enak nič, to pomeni, da je rešitev resnično število. Ta primer ustreza zadnjem dveh primerih prejšnjega seznama.

Kako se izračunajo rešitve kvadratne enačbe?

Za izračun rešitev kvadratne enačbe se uporablja formula, znana kot "ločljivost", ki pravi, da so rešitve enačbe Ax²+Bx+C = 0 podane z izrazom naslednje slike:

Količina, ki se pojavi znotraj kvadratnega korena, se imenuje diskriminator kvadratne enačbe in je označen s črko "D".

Kvadratna enačba bo imela:

-Dve resnični rešitvi Da, in samo da, D> 0.

-Ponavljana resnična rešitev, če in samo če, d = 0.

-Zero Real Solutions (ali dve kompleksni rešitvi), in samo da, D<0.

Primeri

-Rešitve enačbe x²+x-2 = 0 so podane z:

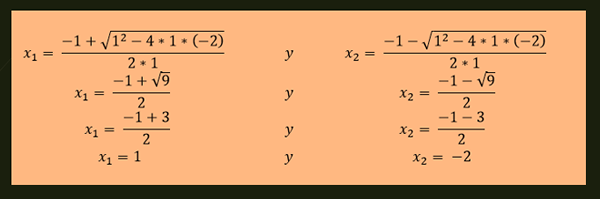
-Enačba x²-4x+4 = 0 ima ponavljajočo se rešitev, ki je podana z:

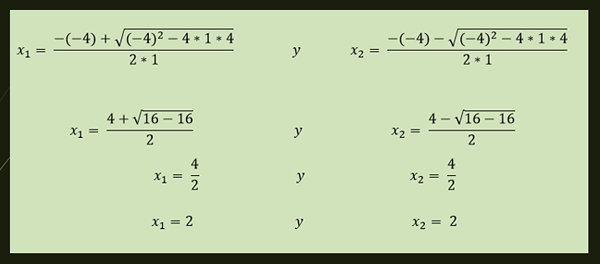
-Raztopine enačbe x²+1 = 0 so podane z:

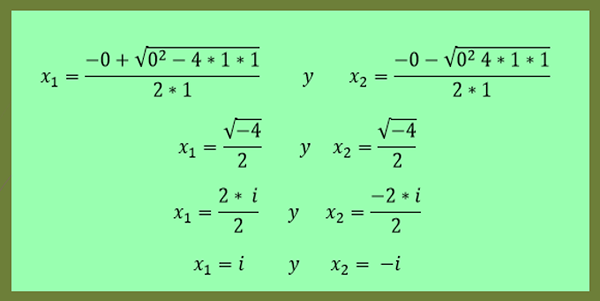
Kot je razvidno iz tega zadnjega primera, je X2 konjugat X1.