Proporcionalnost konstanta, kar je, izračun, vaje

The konstantna sorazmernost Gre za relacijski numerični element, ki se uporablja za opredelitev vzorca podobnosti med dvema velikosti, ki sta hkrati spremenjeni. Zelo pogosto ga je predstavljati kot generično linearno funkcijo z izrazom f (x) = k.X. Vendar to ni edina predstavitev možne sorazmernosti.

Na primer, razmerje med x in y v funkciji y = 3x ima konstanto sorazmernosti, ki je enaka 3. Pokaže, da ko raste neodvisna spremenljivka x, tako tudi odvisna spremenljivka in v trojki svoje prejšnje vrednosti.

Spremembe, uporabljene v eni spremenljivki, imajo na drugi takojšnji posledici, tako da obstaja vrednost, znana kot konstanta sorazmernosti. To služi za povezavo različnih velikosti, ki jih pridobita obe spremenljivki.

[TOC]

Kakšna je konstanta sorazmernosti in tipov

Glede na trend spreminjanja spremenljivk je mogoče proporcionalnosti razvrstiti v dve vrsti.

Neposredna sorazmernost

Predlaga enosmerno razmerje med dvema velikostima. Če neodvisna spremenljivka predstavlja določeno rast, bo tudi odvisna spremenljivka rasla tudi. Podobno bo vsako zmanjšanje neodvisne spremenljivke povzročilo zmanjšanje obsega in.

Na primer linearna funkcija, uporabljena v uvodu; Y = 3x, ustreza neposrednemu razmerju sorazmernosti. To je zato, ker bo povečanje neodvisne spremenljivke x povzročilo povečanje trojne v prejšnji vrednosti, ki jo je sprejela odvisna spremenljivka in.

Podobno se bo odvisna spremenljivka potrojila, ko se X spusti v velikosti.

Vrednost konstantne proporcionalnosti "k" v neposrednem razmerju je opredeljena kot k = y/x.

Obratna ali posredna sorazmernost

Pri tej vrsti funkcij je razmerje med spremenljivkami predstavljeno na antonimni način, kjer rast ali zmanjšanje neodvisne spremenljivke ustreza zmanjšanju ali rasti odvisne spremenljivke.

Lahko vam služi: razgradnjo naravnega števila (primeri in vaje)

Na primer, funkcija f (x) = k/x je obratno ali posredno razmerje. Ker se vrednost neodvisne spremenljivke začne povečevati, bo vrednost K razdeljena z vse večjo številko, zaradi česar je odvisna spremenljivka znižanje vrednosti glede na delež.

Glede na vrednost, ki jo prevzame K, je mogoče opredeliti težnjo proporcionalne inverzne funkcije. Če je K> 0, se bo funkcija v vseh realnih številkah zmanjševala. In njegov graf bo nameščen v 1. in 3. kvadrantu.

Nasprotno, če je vrednost K negativna ali manjša od nič, se bo funkcija povečala in njegov graf bo v 2. in 4 kvadrantu.

Kako se izračuna?

Obstajajo različni konteksti, kjer bo morda potrebna opredelitev konstante sorazmernosti. V različnih primerih bodo prikazani različni podatki o težavi, kjer bo preučevanje le -teh končno pokazalo vrednost K.

Na splošen način je mogoče zgoraj navedeno rekapitulirati. Vrednosti K ustrezajo dvema izrazi glede na vrsto prisotne sorazmernosti:

- Neposredno: k = y/x

- Obratno ali posredno: k = y.X

Glede na vaš graf

Včasih bo le graf funkcije znan delno ali v celoti. V teh primerih bo z grafično analizo potrebno določiti vrsto sorazmernosti. Nato bomo morali določiti koordinato, ki omogoča preverjanje vrednosti X in Y, da veljajo za ustrezno K formulo K.

Grafi, ki se nanašajo na neposredne proporcionalnosti, so linearne vrste. Po drugi strani se grafi inverznih proporcionalnih funkcij običajno oblikujejo hiperbole.

V skladu s tabelo vrednosti

V nekaterih primerih obstaja tabela vrednosti z vrednostmi, ki ustrezajo vsaki ponovitvi neodvisne spremenljivke. Običajno to pomeni realizacija grafa poleg definiranja vrednosti k.

Vam lahko služi: frekvenčna porazdelitev: kako narediti tabelo, na primer vadbo

Glede na analitično izražanje

Prikazuje izraz, ki analitično definira. Neposredno je lahko vrednost k jasna, ali pa se lahko tudi iz samega izraza sklepa.

Praviloma treh neposrednih ali sestavljenih

V drugih modelih vadbe obstajajo določeni podatki, ki se nanašajo na razmerje med vrednostmi. Zaradi tega je treba uporabiti tri neposredne ali spojine za določitev drugih potrebnih podatkov v letu.

Zgodovina

Koncept sorazmernosti je bil vedno prisoten. Ne samo v mislih in delu velikih matematikov, ampak v vsakdanjem življenju prebivalstva, zaradi svoje praktičnosti in uporabnosti.

Zelo pogosto je izpolnjevati situacije, ki zahtevajo pristop sorazmernosti. Te so predstavljene v vsakem primeru, ko se primerjajo spremenljivke in pojave, ki ohranjajo določena razmerja.

Skozi časovnico lahko označimo zgodovinske trenutke, v katerih so bili uporabljeni matematični napredek glede sorazmernosti.

- Drugo stoletje a.c. Sprejet je sistem za shranjevanje deleža in razmer v Grčiji.

- 5. stoletje a.c. V Grčiji je odkrit tudi delež, ki se nanaša na stran in diagonalo kvadrata.

- 600 a.c. Tales de Mileto predstavlja svojo teoremo o sorazmernosti.

- Leto 900. Decimalni sistem, ki ga je Indija prej uporabljala v razlogih in razmerjih. Prispevek Arabcev.

- Xvii stoletje. Prispevki se nanašajo na deleže pri izračunu Eulerja.

- Xix stoletje. Gauss ponuja koncept zapletenega števila in deleža.

- Dvajseto stoletje. Sorazmernost kot funkcijski model določata sladkor in deulofeo.

Rešene vaje

Vaja 1

Mora izračunati vrednost spremenljivk x, y, z in g. Poznavanje naslednjih sorazmernih odnosov:

3x + 2y - 6z + 8g = 1925

Vam lahko služi: neprekinjena naključna spremenljivka

x/3 = y/8 = z/3 = g/5

Relativne vrednosti konstante sorazmernosti so opredeljene. Te je mogoče dobiti iz drugega razmerja, kjer vrednost, ki deli vsako spremenljivko, kaže na odnos ali razlog v zvezi s K.

X = 3k y = 2k z = 3k g = 5k

Vrednosti se nadomestijo v prvem izrazu, kjer bo nov sistem ovrednoten v eni K spremenljivki K.

3 (3K) + 2 (2K) - 6 (3K) + 8 (5K) = 1925

9K + 4K -18K + 40K = 1925

35K = 1925

K = 1925/35 = 55

S to vrednostjo konstante sorazmernosti najdemo sliko, ki določa vsako od spremenljivk.

x = 3 (55) = 165 y = 2 (55) = 110

Z = 3 (55) = 165 g = 5 (55) = 275

Vaja 2

Izračunajte konstanto sorazmernosti in izraz, ki definira funkcijo, glede na njegovo grafiko.

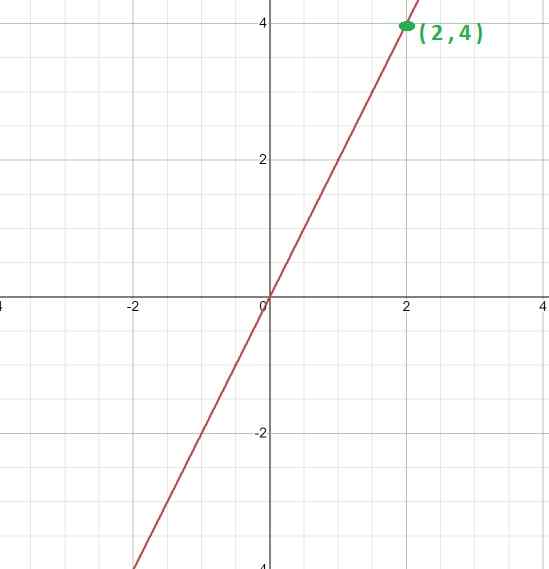
Prvič, graf je analiziran, njegov linearni značaj pa je razviden. To kaže, da gre za funkcijo z neposredno sorazmernostjo in da bo vrednost K pridobljena z izrazom k = y/x

Potem je izbrana določljiva točka grafa, to je ena, v kateri so koordinate, ki ga sestavljajo.

V tem primeru je točka (2, 4). Kje lahko vzpostavimo naslednje razmerje.

K = 4/2 = 2

Tako da je izraz opredeljen s funkcijo y = kx, kar bo za ta primer

F (x) = 2x

Reference

1. Matematika za elektriko in elektroniko. Doktor. Arthur Kramer. Cengage Learning, 27. julij. 2012
2. Vizija 2020: Strateška vloga operativnih raziskav. N. Ravichandran. Zavezniški založniki, 11. septembra. 2005
3. Slovno in aritmetično znanje državnega upravnega pomočnika.e-knjiga. Nori edaformacija
4. Okrepitev matematike za podporo in diverzifikacijo učne načrte: za podporo in diverzifikacijo učne načrte. Mª lourdes lázaro soto. Narcea Ediciones, 29. avgusta. 2003
5. Logistiko in komercialno upravljanje. Maria José Escudero Serrano. Paraninfo Editions, s.Do., 1. septembra. 2013