Koncept in formule stiskanja, izračun, primeri, vaje

The Napor stiskanja ali stiskanja To je sila na enoto območja, katere rezultat je, da predmet potisnete, zategnite ali stisnete, da ga skrajšate. Matematično je:

E = f /a

Tukaj In Označujejo trud, F velikost sile in Do Območje, na katerem je enota v mednarodnem sistemu, če je Newton/M² o Pascal (PA). Napor za stiskanje je normalen napor, Ker je sila, ki jo proizvaja.

Slika 1. Kolumni v akropoli Aten so podvrženi stiskanju. Vir: Pixabay.

Takšen napor lahko stisne predmet ali nasprotno, ga zategnejo in raztegnejo, kot je uporabljeno. V primeru stiskanja se sile uporabljajo v nasprotni smeri, da bi vplivali na zategovanje in skrajšanje predmeta.

Ko sile prenehajo, se veliko materialov vrne v svoje prvotne dimenzije. Ta lastnost je znana po imenu elastičnost. Medtem ko se to zgodi, je enotna elastična deformacija, ki jo je trpel material, ki je podvržen prizadevanju,:

Enotna deformacija = (končna velikost - začetna velikost)/začetna velikost

Deformacija je lahko linearna, površna ali prostornina, čeprav deformacija enote nima enot. Vendar pa so informacije, ki jih ponuja, zelo pomembne, saj ni isto deformiranje 10 m dolge palice v 1 cm, da se deformira 1 cm še 1 m dolga palica.

V elastičnem materialu sta deformacija in trud sorazmerna, v skladu z Hookeovim zakonom:

Trud ∝ Enotna deformacija

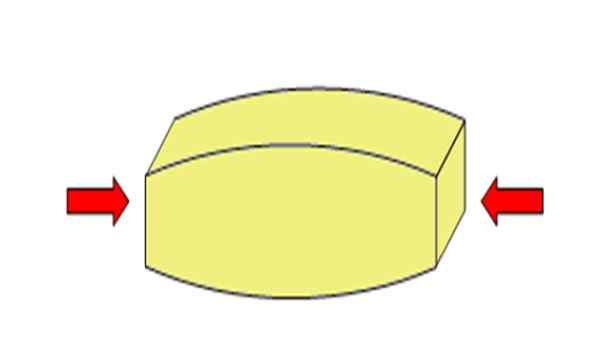Slika 2. Napor za stiskanje zmanjšuje dolžino predmeta. Vir: Wikimedia Commons. Adre-es [cc by-sa 4.0 (https: // creativeCommons.Org/licence/by-sa/4.0)].[TOC]

¿Kako izračunati stiskanje?

Zaradi stiskanja se delci materiala približajo in še več, skrajšajo njihovo velikost. Odvisno od smeri, v katero se prizadevanje uporabi, bo prišlo do skrajšanja ali zmanjšanja katere koli od njegovih dimenzij.

Vam lahko služi: kvantni mehanski model atoma

Začnimo s predpostavko tanke palice originalne dolžine L,  na katero se uporablja normalen napor velikosti In. Če je napor stiskanje, bar doživi zmanjšanje svoje dolžine, označeno s δ. Če je napetost, se bo palica podaljšala.

Seveda je gradivo, iz katerega je element izdelan, odločen v svoji sposobnosti podpore prizadevanjem.

Te elastične značilnosti materiala so vključene v zgoraj omenjeno konstanto sorazmernosti. Je poklican modul elastičnosti tudi Mladi modul in je označeno kot in. Vsak material ima modul elastičnosti, ki se eksperimentalno določi z laboratorijskimi testi.

S tem v mislih, trud In Izraženo je na matematičen način:

Trud ∝ Enotna deformacija

Nazadnje je za določitev tega pogoja kot enačbo potrebna konstanta sorazmernosti, da simbol sorazmernosti ∝ in ga nadomesti z enakostjo, kot je ta:

Napor = sorazmernost konstantna deformacija x enote        

E = y. (Δ /L)

Količnik (Δ /L) To je enotna deformacija, označena kot ε in z δ = Končna dolžina - začetna dolžina. Na ta način trud In Ostane kot:

E = y. ε

Ker je deformacija enote brezdimenzionalna, enote In so enaki tistim In: N/m² ali PA v sistemu SI, funtov/v² o PSI v britanskem sistemu, pa tudi druge kombinacije moči in površin, kot je kg/cm².

Modul elastičnosti različnih materialov

Vrednosti in se v laboratoriju v nadzorovanih pogojih določijo eksperimentalno. Nato modul elastičnosti za materiale, ki se široko uporabljajo pri gradnji, in tudi za kosti:

Vam lahko služi: vektorji v vesolju: kako graditi, aplikacije, vaje

Tabela 1

Material	Modul elastičnosti y (pa) x 109
Jeklo	200
Likalnik	100
Medenina	100
Bronza	90
Aluminij	70
Marmor	petdeset
Granit	Štiri. Pet
Beton	dvajset
Kost	petnajst
Pinewood	10

Primeri

Prizadevanja za stiskanje delujejo na različnih strukturah; Enako, ki je podvrženo delovanju sil, kot je teža vsakega od elementov, ki jih sestavljajo, pa tudi sile zunanjih agentov: veter, sneg, druge strukture in drugo.

Običajno je, da je večina struktur zasnovana tako, da se upira vsem vrstam brez deformiranja. Zato je treba upoštevati stiskanje, da se kos ali predmet ne bo izgubil.

Tudi kosti okostja so strukture, ki so podvržene različnim prizadevanjem. Čeprav so kosti odporne nanje, ko se mejo elastike presežejo po naključju, izvirajo razpoke in zlomi.

Stolpci in stebri

Stolpci in stebri stavb morajo biti narejeni tako, da se upirajo stiskanju, sicer se nagibajo. To je znano kot bočna fleksija tudi Zapletanje.

Stolpci (glej sliko 1) so elementi, katerih dolžina je veliko večja v primerjavi s površino njegovega preseka.

Cilindrični element je stolpec, ko je njegova dolžina enaka ali večja od desetkrat večji od premera preseka. Če pa presek ni konstanten, bo njegov manjši premer sprejet za razvrščanje elementa kot stolpec.

Stoli in banke

Ko se ljudje usedejo v pohištvo, kot so stoli in banke, ali dodajo predmete na vrhu, so noge podvržene stiskanju, ki ponavadi zmanjšujejo njihovo višino.

Slika 3. Ko sedijo, ljudje na stolu prizadevajo za stiskanje, kar ponavadi skrajša njihovo višino. Vir: Pixabay.

Običajno je pohištvo narejeno tako, da se zelo dobro upira teži in se vrne v svoje naravno stanje, ko ga odstranimo. Če pa je velika teža nameščena v krhkih stolih ali bregovih, noge pridejo do stiskanja in se zlomijo.

Vam lahko služi: električni vodniki

Vaje

- Vaja 1

Imate palico, ki prvotno meri dolžino 12 m, na katero je podvržena stiskanju, tako da je njegova enotna deformacija -0.0004. Kakšna je nova dolžina palice?

Rešitev

Začenši iz zgoraj navedene enačbe:

ε = (Δ /l) = - 0.0004

Ja L_F To je zadnja dolžina in L_tudi začetna dolžina, ker Δ = l_F - L_tudi  Imaš:

(L_F - L_tudi)/ L_tudi = -0.0004

Zato: L_F - L_tudi = -0.0004 x 12 m = -0.0048 m. In končno:

L_F  = (12 - 0.0048) M = 11.9952 m.

- Vaja 2

Trdna jeklena palica, valjasta, meri 6 m in premera 8 cm. Če je vrstica podvržena stiskanju z 90 obremenitvijo.000 kg, poiščite:

a) Obseg stiskanja v Megapascalu (MPA)

b) koliko se je zmanjšala dolžina palice?

Rešitev

Najprej je območje A preseka palice, ki je odvisen od njegovega premera D, kar ima za posledico:

A = π. D² / 4 = π. (0.08 m)² / 4 = 5.03 x 10^-3 m²

Sila je takoj, skozi F = m.G = 90.000 kg x 9.8 m/s²= 882.000 n.

Končno se povprečni napor izračuna na naslednji način:

E = f/ a = 882.000 N/ 5.03 x 10^-3 m² = 1.75 x 10⁸ PA = 175 MPA

Rešitev b

Zdaj se uporablja enačba za trud, saj ve, da ima material elastičen odziv:

E = y. (Δ /L)

Modul jekla je v tabeli 1:

Δ = e.L / y = 6 m x 1.75 x 10⁸ PA / 200 x 10 ⁹ Pa = 5.25 x 10 ^-3 M = 5.25 mm.

Reference

1. Pivo, f. 2010. Mehanika materialov. 5. Izdaja. McGraw Hill.
2. Giancoli, d.  2006. Fizika: načela z aplikacijami. 6^Tth  Ed. Dvorana Prentice.
3. Hibbeler, R.C. 2006. Mehanika materialov. 6. Izdaja. Pearson Education.
4. Tippens, str. 2011. Fizika: pojmi in aplikacije. 7. izdaja. McGraw Hill
5. Wikipedija. Stres (mehanika). Okreval od: Wikipedia.org.