Koncept koeficienta koncepcije, formula, izračun, primer

On Koeficient vračila To je količnik med relativno hitrostjo hitrosti in relativno hitrostjo približevanja dvema telesom, ki se trčita. Ko so trupla združena po trčenju, je ta količnik ničen. In enota je vredna, če je trčenje popolnoma elastično.

Recimo dve sferi s trdno maso M1 in masa M2 oziroma, da trpijo. Tik pred trkom so bile sfere hitrosti V1 in V2 Glede določenega inercialnega referenčnega sistema. Takoj po trku se njihove hitrosti spremenijo v V1 ' in V2 '.

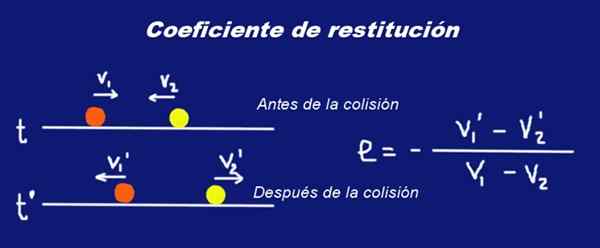Slika 1. Trčenje dveh sfer množic M1 in M2 ter njihov koeficient restitucije in. Pripravil Ricardo Pérez.

Pismo je postavljeno Krepka pisava V hitrostih, ki kažejo, da so vektorske količine.

Poskusi kažejo, da vsak trk izpolnjuje naslednje razmerje:

V1 ' - V2 '= -in (V1 - V2)

Kje in Je resnično število med 0 in 1, imenovano Koeficient vračila trka. Prejšnji izraz se razlaga na naslednji način: 

Relativna hitrost dveh delcev pred trkom je sorazmerna z relativno hitrostjo obeh delcev po trku, konstanta sorazmernosti je (-e), kjer je E koeficient vračila trka.

[TOC]

Za kaj je koeficient restitucije?

Uporabnost tega koeficienta je v poznavanju stopnja neelastičnosti trka. V primeru, da je trčenje popolnoma elastično, bo koeficient 1, v povsem neelastičnem trku pa bo koeficient vreden 0, saj je v tem primeru relativna hitrost po trku nična.

Vzajemno, če so koeficient vračila trka in hitrosti delcev pred njim, potem lahko hitrost predvidi po takšnem trku. 

Vam lahko služi: 13 primerov Newtonovega prvega zakona v resničnem življenju

Zagon

V trkih poleg odnosa, ki ga vzpostavlja koeficient restitucije, obstaja še en temeljni odnos, ki je Ohranjanje zagona.

Zagon str delca ali količine gibanja, kot se imenuje, je produkt mase M delca za svojo hitrost V. To je: zagon str To je vektorski znesek.

V trkih linearni zagon Str Sistem je enak tik pred in po trku, ker je zunanja sila zaničevalna proti kratkim, a intenzivnim silam notranje interakcije med trkom. Toda ohranjanje zagona ni dovolj Str sistema za reševanje splošnega problema trka.

V predhodno omenjenem primeru je napisano tako, kot je ta:

 M1 V1 + M2 V2 = M1 V1 ' + M2 V2 ' .

Če koeficient restitucije ni znan, ni mogoče rešiti težav z trkom. Ohranjanje zagona, čeprav je potrebno, ni dovolj za napovedovanje hitrosti po trčenju.

Ko težava navaja, da se telesa po trku gibljejo skupaj, implicitno pravi, da je koeficient restitucije 0.

Slika 2. V biljardnih kroglicah obstajajo trki koeficienta restitucije malo manj kot 1. Vir: Pixabay.

Koeficient energije in restitucije 

Druga pomembna fizična količina, ki je vključena v trke, je energija. Med trki so izmenjave kinetične energije, potencialne energije in drugih vrst energije, kot je kalorična energija.

Pred in po trku je potencialna energija interakcije praktično nič, zato energetsko ravnovesje vključuje kinetično energijo delcev pred in po in po količini Q imenovana razpršena energija.

Lahko vam služi: Heisenberg Atomski model

Za dve masni sferi M1 in M2, ki trčita energijsko ravnovesje pred in po trku, je napisana tako:

½ m1 V1^2 + ½ m2 V2^2 = ½ m1 V1 '^2 + ½ m2 V2 '^2 + q

Ko so sile za interakcijo med trkom čisto konzervativne, se zgodi, da Skupna kinetična energija Od delcev, ki trkajo, je ohranjen, to je, da je isto pred in po trčenju. Ko se to zgodi, je trčenje popolnoma elastično.

V primerih elastičnih trkov energije ne razprši. In tudi koeficient restitucije je v skladu: E = 1. 

Nasprotno, v neelastičnih trkih, ki ≠ 0 in 0 ≤ e < 1. Sabemos, por ejemplo, que la colisión de las bolas de billar no es perfectamente elástica porque el sonido que se emite durante el impacto es parte de la energía disipada.

Da bi bili problem trka popolnoma določena, je treba vedeti koeficient restitucije ali izmenično količino energije, ki se med trkom razblini.

Koeficient restitucije je odvisen od narave in vrste interakcije med obema telesom med trkom.

Po drugi strani pa bo relativna hitrost teles pred trkom opredelila intenzivnost interakcije in s tem vpliv na koeficient restitucije. 

Kako se izračuna koeficient restitucije?

Za ponazoritev, kako se izračuna koeficient vračila trka, bomo vzeli preprost primer:

Recimo, da trk dveh masnih sfer M1 = 1 kg in M2 = 2 kg ta premik na ravno trenje (kot na sliki 1).

Prva sfera vpliva na začetno hitrost V1 = 1 m/s Približno drugega, ki je prvotno v mirovanju, to je V2 = 0 m/s.

Lahko vam služi: prvi zakon termodinamike: formule, enačbe, primeri

Po trku se premikajo takole: prvi se ustavi (V1 '= 0 m/s) in drugi se s hitrostjo premakne v desno V2 '= 1/2 m/s.

Za izračun koeficienta restitucije v tem trčenju uporabimo razmerje:

V1 ' - V2 ' = -in ( V1 - V2 ) 

0 m/s - 1/2 m/s = - e (1 m/s - 0 m/s) => - 1/2 = - e => e = 1/2 .

Primer

V enem dimenzionalnem trku obeh sfer prejšnjega oddelka je bil izračunan njegov restitucijski koeficient, kar je povzročilo E = ½ .

Ker e ≠ 1 trk ni elastičen, to je, kinetična energija sistema ni ohranjena in obstaja nekaj razpršene energije q (na primer ogrevanje kroglic zaradi trka).

Določite vrednost, razpršeno v Joulesu. Izračunajte tudi odstotni del razpršene energije.

Rešitev

Začetna kinetična energija sfere 1 je: 

K1i = ½ m1 v1^2 = ½ 1 kg (1 m/s)^2 = ½ j

Medtem ko je Sphere 2 nič, ker je bil sprva v mirovanju.

Torej je začetna kinetična energija sistema Ki = ½ j.

Po trku se samo druga sfera premakne s hitrostjo v2 '= ½ m/s, tako da bo končna kinetična energija sistema:

Kf = ½ m2 v2 '^2 = ½ 2 kg (½ m/s)^2 = ¼ j J

To pomeni, da je energija, razpršena v trku,:

Q = ki - kf = (½ j - ¼ j) = 1/4 j

In del energije, razpršenega v tem trčenju, se izračuna na naslednji način:

F = q / ki = ¼ / ½ = 0,5, kar pomeni, da je bilo 50% energije sistema razpršeno zaradi neelastičnega trka, katerega koeficient restitucije je 0,5.

Reference

1. Bauer, w. 2011. Fizika za inženiring in znanosti. Zvezek 1. MC Graw Hill.
2. Figueroa, d. 2005. Serija: Fizika za znanost in inženiring. Zvezek 1. Kinematika. Uredil Douglas Figueroa (USB).
3. Vitez, r. 2017. Fizika za znanstvenike in inženiring: strateški pristop. Pearson.
4. Sears, Zemansky. 2016. Univerzitetna fizika s sodobno fiziko. 14. Ed. Zvezek 1.
5. Wikipedija. Količina gibanja.Okrevano od: je.Wikipedija.org.