Kako pridobiti odstotek? Primeri in vaje

Pločevinka Pridobite odstotek Z več metodami. 10% katere koli številke lahko hitro izračunate samo, če premikate svojo decimalno vejico v levi strani. Na primer, 10% od 100 je 10; 10% od 1000 je 100.

Če želite izračunati bolj zapletene odstotke, na primer 36% od 25 ali 250% od 20, so potrebne druge metode. Za primere, ko 10 -odstotni sistem ni uporaben, je mogoče upoštevati naslednje metodologije.

Slika 1. Popusti z različnimi odstotki. Koliko se prihranimo?. Vir: Pixabay.

Izraz odstotek pomeni določen del na vsakih sto in se nanaša na aritmetično operacijo, ki se izvaja za iskanje omenjenega dela. Na primer, 20% ("dvajset odstotkov") se bere v pesosu, to pomeni, da je 20 pesosov popust na vsakih 100 pesosov.

Odstotek služi za izračun, kateri del skupne vrednosti predstavlja znesek. V tem primeru se skupna vrednost prevzame na lestvici 100 in odstotek sporoča, koliko je na podlagi teh 100 del, ki ga je treba izračunati.

Poglejmo, kako je to storjeno s temi primeri. V prvi vrsti to počnemo v obliki dela:

• 20% = 20/100
• 5% = 5 /100
• 0,7% = 0,7 / 100
• 100% = 100 /100

Upoštevajte, da je 100% enako 1. Toda odstotke je mogoče zapisati tudi decimalno:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

Ko je odstotek določene številke izražen, preprosto Vejica se premika Od teh krajev na levi strani. V odstotkih pravilo sorazmernosti:

20% je 20 od 100, zato:

20% od 100 je 20, 20% od 200 je 40, 20% 300 je 60, 20% od 50 je 10.

Splošno pravilo za 20 % katerega koli zneska

20% x je x *(20/100) = x *0,2 = 0,2 *x

To pravilo se zlahka razširi in poišče kateri koli drugi odstotek, ki je zaželen. Poglejmo, kako v naslednjem razdelku.

Vaja, razrešena s formulo za izračun n% 

Formula, ki jo lahko povzamemo čim prej in hitro izračunamo kakršen koli odstotek n je:

n % =(A * n)/100

Na primer, želite izračunati 25% od 400

Potem n = 25 in a = 400, kar ima za posledico (400*25)/100 = 100

Primer

Kolikšen odstotek 60 je 24?

Rešitev

Kar je zahtevano, je enako vprašanju, kaj je N% od 60, ki daje 24?

Predlagamo splošno formulo:

60 * n / 100 = 24

Počistimo n S tem postopkom:

-100, ki se deli na člana IZiédo Enakosti, pojdite k članu prav pomnoževanje. 

-In 60, ki se pomnoži v članu levo Pojdi k članu prav delitev.

N = 24 *100 /60 = 2400 /60 = 240/6 = 6 *40/6 = 40

Ugotovljeno je, da je 40% od 60 24.

Rešene odstotne vaje za izračun 

Spodaj so preproste vaje za začetek vadbe omenjenih.

Lahko vam služi: 15 najbolj priljubljenih legendov in mitov

Vaja 1

Poiščite 50% od 90.

Rešitev

Tukaj x = 90, n = 50 % in zamenjajte:

90 * 50% = 90 * (50 /100) = 4500 /100 = 45 

To je povsem preprosto, saj je 50 % katerega koli zneska polovica tega zneska, polovica 90 pa 45.

Vaja 2

Poiščite 30% od 90.

Rešitev

90 * 30% = 90 * (30/100) = 2700 /100 = 27

Odstotek se poveča

V vsakdanjem življenju je pogosto poslušati povečanje nečesa, na primer povečanje proizvodnje, zvišanje plač ali porast izdelka. Skoraj vedno je izražen v odstotni obliki.

Na primer, določen izdelek stane 300 EUR, vendar je doživel 30% povečanje. Vprašamo se: kakšna je nova cena izdelka?

Prva je izračunati del, ki ustreza povečanju. Ker je povečanje 30 delov od 100, je povečanje povečanja, ki temelji na prvotni ceni 300, trikrat večji od 30 delov, to je 3*30 = 90.

Izdelek se je povečal za 90 EUR, zato bo nova končna cena tisto, kar je stalo povečanje prej:

Nova cena = stara cena + 90 € = 390 €

Lahko sestavimo formulo za izračun povečanja odstotka. Pisma uporabljamo za simbolizacijo cen, kot je ta:

-F je končna vrednost

-Yo je začetna vrednost in

-n je povečanje povečanja.

S temi imeni bi bila končna vrednost izračunana tako:

f = i + (i* n / 100)

Ampak kako Yo Ponavlja se v obeh pogojih, lahko jemljemo kot skupni dejavnikZa pridobitev tega drugega izraza, enako veljaven:

F = i * (1 + n / 100)

Preverimo s že rešenim primerom, izdelek, ki je stal 300 € in povečal 30%. Tako poskrbimo, da formula dobro deluje:

Končna cena = f = 300 € * (1 + 30/100) = 300 * (1 + 0,3) = 300 * 1,3 = € 390

Vaja 3

Zaposleni je zaslužil 1500 EUR, a je bil napredovan in njegova plača je imela 20 -odstotno povečanje. Kakšna je vaša nova plača?

Rešitev

Uporabimo formulo:

F = 1500 € * (1 + 20/100) = € 1500 * (1 + 0,2) = € 1500 * 1,2 = € 1800

Nova plača zaposlenih znaša 1800 €.

Odstotek se zmanjšuje

V primeru zmanjšanja formula za izračun končne vrednosti F določenega začetnega zneska Yo To je utrpelo zmanjšanje n% je:

F = i * (1 - n / 100)

Treba je opozoriti, da je bil pozitivni znak (+) formule v prejšnjem razdelku nadomeščen z negativnim znakom (-).

Slika 2. Obvestilo o odstotkih popusta. Vir: Pixabay

Vaja 4

Izdelek z 800 €, vendar je prejel 15% popust. Kakšna je nova cena izdelka?

Rešitev 4

Končna cena po formuli je:

F = 800 € * (1 - 15/100) = € 800 * (1 - 0,15) = € 800 * (0,85) = € 680

Končna cena s 15 -odstotnim popustom znaša 680 EUR, kar predstavlja prihranek v višini 120 €.

Zaporedni odstotki

Pojavi se, ko nekaj zneska utrdi odstotno spremembo in nato uporabi drugo, tudi odstotek. Na primer izdelek, ki je imel dva odstotna popusta zapored. Drug primer je zaposleni, ki je imel dva zaporedna povišanja plač.

Vam lahko služi: pomembnejše gospodarske dejavnosti Yucatana

- Zaporedni odstotek se poveča

Baza rešitev teh primerov je enaka edinstvenim povečanjem, vendar je treba upoštevati, da se drugi odstotek poveča na končni vrednosti prvega povečanja.

Recimo, da je izdelek, ki se je dvignil najprej 10%, in nato 5%. Nepravilno je reči, da se je povečal za 15%, dejansko je bil več kot ta odstotek.

Formule za končno vrednost bi veljale tako:

-Najprej se izračuna končna vrednost prvega povečanja N1%

f1 = i + i * n1 / 100

-In nato, da bi našli končno vrednost drugega povečanja N2%, se končna vrednost F1 jemlje kot začetna vrednost. Zato:

F2 = f1 + f1 * n2 /100 

Vaja 5

Knjiga je prvotno stala 55 evrov, vendar je zaradi uspeha in velikega povpraševanja doživela dva zaporedna povišanja prvotne cene. Prvo povečanje je bilo 10%, drugo pa 20%. Kakšna je končna cena knjige?

Rešitev

-Prvo povečanje:

F1 = € 55 * (1 + 10/100) = € 55 * 1,1 = 60,5 €

-Drugo povečanje

F2 = 60,5 € * (1 + 20/100) = 60,5 * 1,2 = 72,6

Končna cena je 72,6 €.

Vaja 6

V zvezi s prejšnjo vajo. Dva zaporedna povečata: v kolikšen odstotek edinstvenega povečanja glede prvotne knjige ustreza?

Rešitev

Če pokličemo N% na odstotek edinstvenega povečanja, je formula, ki povezuje ta edinstven odstotek na prvotno vrednost in končna vrednost je:

F2 = i *(1 + n / 100) 

To pomeni:

72,6 € = 55 € + 55 € * (n / 100)

Če želite povečanje povečanja N% = (n /100), imamo:

(N / 100) = (72,6 € - 55 €) / 55 € = 17.6 € / 55 € = 0,32

Zato:

N = 0,32 * 100 = 32

Po ceni knjige je bil uporabljen skupni odstotek za 32%. Upoštevajte, da je to povečanje večje od vsote dveh zaporednih odstotkov.

- Zaporedni odstotni popusti

Ideja je podobna kot pri zaporednem odstotku. Drugi odstotni popust je treba vedno uporabiti za končno vrednost prvega popusta, poglejmo primer:

Vaja 7

10 -odstotni popust, ki mu sledi drugi popust v višini 20% na predmetu, na katerega je edinstven odstotek popusta enakovreden?

Rešitev

-Prvi popust:

F1 = i - i * n1 / 100  

-Drugi popust

F2 = f1 - f1 * n2 / 100

Zamenjava prve enačbe v drugem ostane:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Če razvijamo ta izraz, dobimo:

f2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Risanje skupnega faktorja Yo:

f2 = i * (1- n1% - n2% + n1% * n2%)

Končno se nadomestijo odstotki, navedeni v vprašanju:

F2 = i * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = i * (1 - 0.28) = i * (1 - 100 /100) = i * (1 - 28%)

Z drugimi besedami, zaporedni popusti v višini 10% in 20% ustrezajo edinstvenemu 28 -odstotnemu popustu.

Napredne vaje

Poskusimo s temi vajami le, če so bile ideje prejšnjih dovolj jasne.

Lahko vam služi: enostavne in čudovite naslovnice za geografijo, platnice, slike

Vaja 8

Osnova trikotnika meri 10 cm in višino 6 cm. Če se osnovna dolžina zmanjša za 10%?

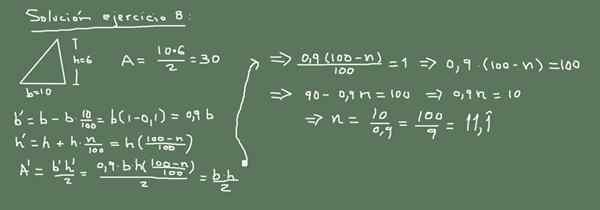Slika 3. Alternativna rešitev za vajo 8. Pripravil f. Zapata.

Rešitev 8

Prvotno območje trikotnika je:

A = (10cm * 6cm) / 2 = 30 cm²

Če se osnova zmanjša za 10%, potem je njegova nova vrednost:

Nova baza = 10 - (10/100) x 10 = 9 cm.

Nova vrednost višine bo x, prvotno območje pa mora biti nespremenjeno, tako da:

(9cm * x) /2 = 30 cm²

Potem se vrednost x očisti kot:

X = 60 cm² / 9 cm = (20/3) cm = 6.666 cm

Kar pomeni povečanje za 0,666 v primerjavi s prvotno vrednostjo. Poglejmo zdaj, kolikšen odstotek tega predstavlja:

6,666 = 6 + (6 * n/100) 

6,666 -6 = 6 * n/100

0.666 = 6 * n/100

N/100 = 0,111

N = 11.1

Odgovor je: višina je treba povečati za 11,1%, da območje trikotnika ostane enako.

Vaja 9

Če se plača zviša za 20%, potem pa davčni popust 5%, kaj je resnično povečanje, ki ga prejme delavec?

Rešitev 

Najprej izračunamo povečanje N1%:

f1 = i + i * n1 / 100

Nato uporabimo popust N2%:

F2 = f1 - f1 * n2 / 100

Prva enačba je zamenjana v drugem:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

Prejšnji izraz se razvija:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Končno je odstranjen Yo Skupni faktor in vrednosti N1 = 20 in N2 = 5, ki se pojavijo v izjavi, se nadomestijo:

F2 = i (1 + 0,2 - 0,05 - 0,2* 0,05) = i* (1 + 7/50) = i* (1 + 14/100) = i* (1 + 14%)

Delavec je prejel neto porast za 14%.

Vaja 10

Odločite se, kaj je med tema dvema možnostma najbolj priročno:

i) pridobiti T -majice z 32 % popustom.

Ii) kupite 3 t -majice za ceno 2.

Rešitev 

Vsako možnost analiziramo posebej in nato izberemo najbolj ekonomično:

i) Naj bo X trenutna cena majice, 32 -odstotni popust predstavlja končno ceno XF:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Na primer, nakup 3 majic pomeni porabo 3 x 0.68 x = 2.04x

ii) Če je x cena majice, za 3 majice preprosto plačate 2x.

Recimo, da je majica vredna 6 evrov, z 32 -odstotnim popustom bi bil vreden 4.08 EUR. Nakup 1 t -majice ni veljavna možnost v ponudbi 3 × 2. Če želite kupiti samo 1 majico, je popust zaželen.

Če pa želite kupiti na desetine, je ponudba 3 × 2 le malo cenejša. Na primer, 6 t -majic s popustom bi šlo za 24.48 evrov, medtem ko bi s ponudbo 3 × 2 stali 24 evrov

Reference

1. Enostavna učilnica. Odstotek. Pridobljeno iz: učilnice.com
2. Baldor a. 2006. Praktična teoretična aritmetika. Kulturne izdaje.
3. Otroci Educa. Kako se naučiti izračunati odstotek. Okrevano od: Educapeques.com
4. Gutiérrez, g. Opombe o finančni matematiki. Okreval od: CSH.Izt.UAM.mx
5. Pametni klopi. Odstotek: kaj je in kako se izračuna. Okrevano od: SmartIck.je