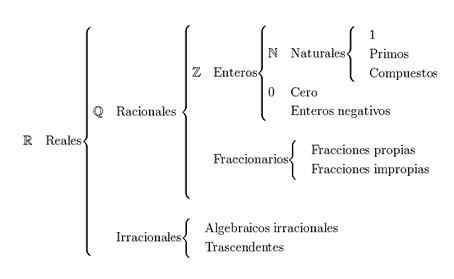
Razvrstitev resničnih številk

Glavni Razvrstitev resničnih številk Razdeljen je na naravne številke, celotne številke, racionalne in iracionalne številke. Resnične številke so predstavljene s črko r.

Realne številke se nanašajo na kombinacijo skupin racionalnih in iracionalnih številk. Za oblikovanje teh skupin so potrebne naravne in cele številke.

Obstaja veliko načinov, kako je mogoče graditi ali opisati različne realne številke, ki se razlikujejo od preprostejših oblik do bolj zapletenih oblik, odvisno od matematičnega dela, ki ga želite opraviti.

Kako so razvrščene realne številke?

- Naravne številke

Naravne številke so predstavljene s črko (n) in so tiste, ki se uporabljajo za štetje (0,1,2,3,4 ...). Na primer "obstaja petnajst Rosas na vrtu "," populacija Mehike je iz 126 milijoni ljudi ali "vsote dva in dva je štiri". Treba je opozoriti, da nekatere klasifikacije vključujejo 0 kot naravno število, druge pa ne. 

Dva otroka, ki izdelujeta vsoto dveh naravnih številk.

Naravne številke ne vključujejo tistih, ki imajo decimalni del. Zato je „prebivalstvo Mehike iz 126.2 Milijoni ljudi "ali" naredijo temperaturo 24.5 Celzija stopinj ”naravnih številk ni bilo mogoče upoštevati.

V skupnem jeziku, kot so osnovne šole, lahko naravne številke imenujemo računovodske številke, da izključijo negativna cela števila in nič.

Naravne številke so baze, s katerimi je mogoče zgraditi veliko drugih sklopov številk: cele številke, racionalne številke, realne in zapletene številke.

Lastnosti naravnega števila, kot sta delitev in porazdelitev primarnih številk, so preučene v teoriji številk. Težave, povezane s štetjem in naročanjem, kot so našteti in delitev, se preučujejo v kombinatorju.

Imajo več lastnosti, kot so: vsota, množenje, odštevanje, delitev itd.

Vam lahko služi: sodobna znanost

Ordinalne in kardinalne številke

Naravne številke so lahko redne ali kardinalne.

Kardinalne številke bi bile tiste, ki se uporabljajo kot naravne številke, kot je omenjeno zgoraj v primerih. "Imeti dva piškotki, "jaz sem oče tri Otroci "," Škatla vključuje dva darilne kreme ". 

Ordinati so tisti, ki izražajo red ali označujejo položaj. Na primer, v dirki je zmagovalec nakazan vrstni red prihoda tekačev in zaključil zadnji, ki je prišel na ciljno črto.

Na ta način bo rečeno, da je zmagovalec "prvi", naslednji "drugi", naslednji "tretji" in tako naprej do zadnjega. Te številke je mogoče predstaviti s črko v zgornji desni strani, da poenostavite pisanje (1., 2., 3., 4., ETC.).

- Celo število številk

Celotne številke so sestavljene iz teh naravnih števil in njihovih nasprotij, torej negativnih številk (0, 1, -1, 2, -2, 50, -50 ...). Tako kot naravne številke tudi ti ne vključujejo tistih, ki imajo decimalni del.

Primer celih števil bi bil "povprečno 30. v Nemčiji", "Ostal sem pri 0, ko sem prišel do konca meseca", "da bi se spustil v klet, morate označiti gumb dvigala" dvigala ".

Celih številk ni mogoče zapisati z delno komponento. Na primer številke, kot je 8.58 ali √2 niso cele številke.

Celotne številke so predstavljene s črko (z). Z je podmorska skupina racionalnih številk, ki posledično tvori skupino resničnih N številk. Tako kot naravne številke je tudi Z je neskončna računovodska skupina.

Cela števila tvorijo najmanjšo skupino in najmanjši nabor naravnih številk. V teoriji algebrskih števil se cele številke včasih imenujejo iracionalno, da jih razlikujejo od algebrskih celih števil.

Lahko vam služi: raziskovalni projekt: zabave, kako je izdelano in primer

- Racionalne številke

Nabor racionalnih števil je predstavljen s črko (q) in vključuje vse tiste številke, ki jih je mogoče zapisati kot delček celih številk.

To pomeni, da ta komplet vključuje naravne številke (4/1), celotne številke (-4/1) in natančne decimalne številke (15,50 = 1550/100).

Porazdelitev 1/6 sira je racionalno število.

Decimalna širitev racionalnega števila se vedno konča po končnem številu števk (npr. 15,50) ali ko se začne isto končno zaporedje števk znova in znova ponavljati (npr. 0,34566666666666…). Zato so znotraj nabora racionalnih številk vključene številke. čisti časopisi ali mešani časopisi.

Poleg tega vsaka ponavljajoča se ali terminalna decimalka predstavlja racionalno število. Te izjave veljajo ne le za bazo 10, ampak tudi za katero koli drugo osnovno številko.

Resnično število, ki ni racionalno, se imenuje iracionalno. Na primer iracionalne številke vključujejo √2, π in e. Ker je celoten sklop racionalnih številk otrplo in da skupina resničnih števil ni otrplo, lahko rečemo, da so skoraj vse realne številke neracionalne.

Racionalne številke je mogoče formalno opredeliti kot enakovredne razrede celih parov (p, q), tako da je Q ≠ 0 ali enakovredno razmerje, ki ga definira (p1, q1) (p2, q2) samo, če je p1, q2 = p2q1.

Racionalne številke, skupaj z vsoto in množenjem, oblikujejo polja, ki sestavljajo celotne številke in jih vsebuje katera koli veja, ki vsebuje celoto.

- Iracionalne številke

Neracionalne številke so vse realne številke, ki niso racionalne številke; Neracionalne številke ni mogoče izraziti kot ulomki. Racionalne številke so številke, sestavljene iz frakcij celih številk.

Zaradi testa s pevcem, ki pravi, da so vse realne številke nerodne in da je racionalno, če gre za številke, lahko sklepamo, da so skoraj vse realne številke iracionalne.

Vam lahko služi: usmeritev in premik

Kadar je polmer dveh segmentov iracionalnega števila, lahko rečemo, da so ti segmenti linij neizmerni; kar pomeni, da ni dovolj dolžine, da bi lahko bil vsak od njih "meril" z več posameznimi celotnimi celotnimi celoviti.

Med iracionalnimi številkami so polmer π kroga kroga do njegovega premera, število Eulerja (E), zlato število (φ) in kvadratni koren dveh; Še več, vse kvadratne korenine naravnega števila so neracionalne. Edina izjema od tega pravila so popolni kvadratki.

Opazimo, da se v številčnem sistemu (na primer decimalne številke), ko se iracionalna števila izražajo.

To pomeni, da ne vsebujejo zaporedja števk, ponavljanja, s katerim se izvede linija.

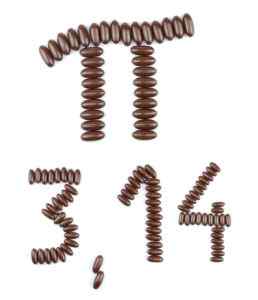Poenostavitev iracionalne številke Pi.

Na primer: decimalna predstavitev številke π se začne s 3.14159265358979, vendar ni končnega števila števk, ki bi lahko natančno predstavljali π, niti jih ni mogoče ponoviti.

Dokaz, da se mora decimalna širitev racionalnega števila končati ali ponoviti, se razlikuje od dokaz, da mora biti decimalno razširitev racionalno število; Čeprav so osnovni in nekoliko dolgi, ti testi vzamejo nekaj dela.

Običajno matematiki na splošno ne sprejemajo pojma o "končnem ali ponavljanju", da bi opredelili koncept racionalnega števila.

Neracionalne številke je mogoče zdraviti tudi z neprekinjenimi frakcijami.

Reference

1. Klasificirane resnične številke. Okreval od čilimata.com.
2. Naravno število. Okreval iz Wikipedije.org.
3. Razvrstitev številk. Ditutor si je opomogel.com.
4. Okreval iz Wikipedije.org.
5. Iracionalna številka. Okreval iz Wikipedije.org.