Lastnosti enotnih celic, rdeča konstanta in vrste

The Enotna celica Je namišljen prostor ali regija, ki predstavlja minimalni izraz celote; Da bi bila v primeru kemije celota kristal, sestavljen iz atomov, ionov ali molekul, ki so naročeni po strukturnem vzorcu.

V vsakdanjem življenju lahko najdete primere, ki utelešajo ta koncept. Za to je treba biti pozoren na predmete ali površine, ki imajo določen ponavljajoči se vrstni red njegovih elementov. Nekaj ​​mozaikov, bas -relief, obrt.

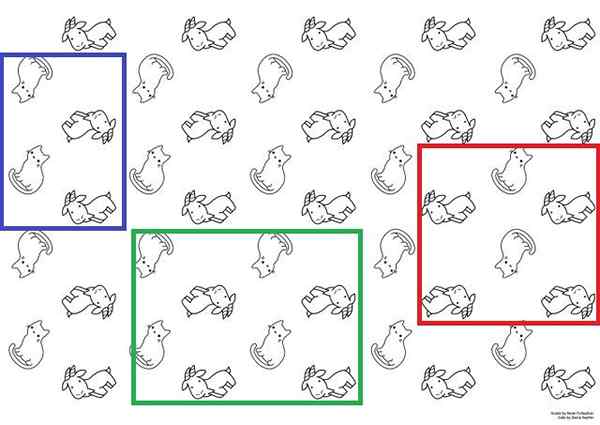Enotne celice na papirju za mačke in koze. Vir: Hanna Petruschat (WMDE) [CC BY-SA 4.0 (https: // creativeCommons.Org/licence/by-sa/4.0)].

Za jasnejšo ponazoritev imate vrhunsko sliko, ki bi jo lahko uporabili kot papir tapiserije. V njem se mačke in koze pojavljajo z dvema alternativnima čuboma; Mačke so noge ali glava, koze pa gledajo navzgor ali navzdol.

Te mačke in koze vzpostavljajo ponavljajoče se strukturno zaporedje. Za izdelavo vsega papirja bi bilo dovolj, da bi enotno celico na površini reproducirali zadostno številokrat s translacijskimi gibi.

Možne enote so predstavljene z modrimi, zelenimi in rdečimi škatlami. Za pridobitev papirja bi lahko uporabili katero koli od teh treh; Vendar jih je treba zamisliti po površini, da ugotovite, ali reproducirajo isto zaporedje, opaženo na sliki.

Začenši z rdečo škatlo, bi bilo cenjeno, da če bi se tri stolpce (mačk in koz) premaknile na levo. Zato bi privedlo do drugega zaporedja in ga ne moremo obravnavati kot enotno celico.

Medtem ko si zamislite, da bi dve škatli premikali modro in zeleno, bi dobili isto zaporedje papirja. Obe sta enotni celici; Vendar modra škatla bolj upošteva definicijo, saj je manjša od zelene škatle.

[TOC]

Lastnosti celic

Njegova lastna definicija poleg na novo pojasnjenega primera pojasnjuje več njegovih lastnosti:

-Če se premikajo v prostoru, ne glede na smer, bomo dobili celotno trdno ali steklo. To je zato, ker, kot je omenjeno pri mačkah in kozah, reproducirajo strukturno zaporedje; ki je enak prostorski porazdelitvi ponavljajočih se enot.

-V primerjavi z drugimi možnimi možnostmi celic morajo biti čim manjši (ali zavzemajo malo prostornine).

Vam lahko služi: metilmalonska kislina: struktura, lastnosti, sinteza, uporaba

-So navadni, simetrični. Prav tako se njegova simetrija dobesedno odraža v kristalih spojine; Če je enotna celica soli kubična, bodo njegovi kristali kubični. Vendar obstajajo kristalne strukture, opisane z enotnimi celicami z izkrivljenimi geometrijami.

-Vsebujejo ponavljajoče se enote, ki jih je mogoče nadomestiti s točkami, ki so v drugem -dedimenzionalno tisto, kar je znano kot mrežica. V prejšnjem primeru mačke in koze predstavljajo retikularne točke, ki jih vidimo z višje ravnine; to je dve dimenziji.

Število ponavljajočih se enot

Ponavljajoče se enote ali retikularne točke enotnih celic ohranjajo enak delež trdnih delcev.

Če se znotraj modre škatle šteje število mačk in koz, bosta dve mački in kozi. Enako velja tudi za zeleno škatlo in z rdečo škatlo (tudi če je že znano, da ni enotna celica).

Recimo na primer, da sta mačke in koze atoma G in C (čudno varjenje živali). Ker je delež med G in C 2: 2 ali 1: 1 v modrem polju, lahko brez napak pričakujemo, da bo trdna snov GC (ali CG) formula.

Kadar ima trdna trdnost bolj ali manj kompaktne strukture, kot pri soli, kovinah, oksidi, sulfidi in zlitinah, v enotnih celicah ni celih ponavljajočih se enot; to pomeni, da obstajajo deli ali deli, ki seštevajo do ene ali dveh enot.

To ne velja za GC. Če bi modra škatla "začela" do mačk in koz v dveh (1/2g in 1/2c) ali štirih delih (1/4g in 1/4c). V naslednjih razdelkih bo razvidno, da so v teh enotnih celicah retikularne točke priročno razdeljene na to in druge načine.

Katere omrežne konstante definirajo enotno celico?

Enotne celice primera GC so dve dimenzionalni; Vendar to ne velja v resničnih modelih, ki upoštevajo tri dimenzije. Tako se polja ali paralelogrami spremenijo v paralelepípedos. Zdaj izraz "celica" prevzame večji smisel.

Dimenzije teh celic ali paralelepiped so odvisne od tega, kako dolgo so njihove strani in koti.

Na spodnji sliki imate spodnji zadnji kotiček vzporednic, sestavljen iz strani do, b in c, in koti α, β in γ.

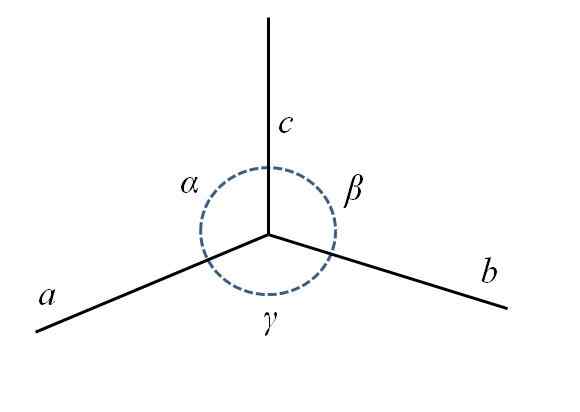Parametri enotne celice. Vir: Gabriel Bolívar.

Kot vidite, do je malo dlje kot b in c. V središču imate krog s pikčasto črto, ki označite kote α, β in γ, med AC, Cb in ba, oziroma. Za vsako enotno celico imajo ti parametri konstantne vrednosti in določajo njihovo simetrijo in preostanek kozarca.

Vam lahko služi: kalcijev peroksid (caO2): lastnosti, tveganja in uporabe

Če ponovno uporabimo nekaj domišljije, bi parametri slike opredelili celico, podobno raztegnjeni kocki na robu do. Tako se enotne celice pojavljajo z različnimi dolžinami in koti njegovih robov, ki jih je mogoče razvrstiti tudi v različne vrste.

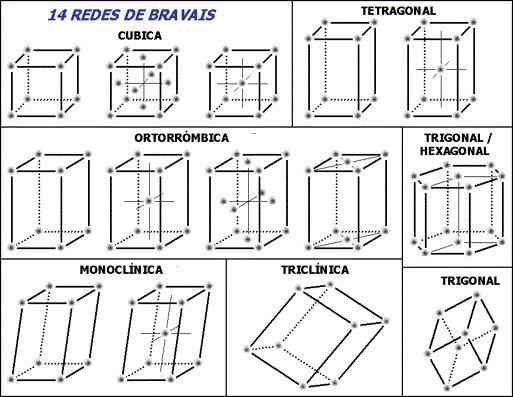
Fantje

14 Bravais Networks in sedem osnovnih kristalnih sistemov. Vir: Originalni nalagalnik je bil jezen na portugalski Wikipediji. [CC BY-SA 3.0 (http: // creativeCommons.Org/licence/by-sa/3.0/]]

Opomba, da zaženete pikčaste črte znotraj enotnih celic: označujejo spodnji zadnji kot, kot je razloženo. Naslednje vprašanje je mogoče postaviti, kje so retikularne točke ali ponavljajoče se enote? Čeprav dajejo napačen vtis, da so celice prazne, v svojih točkah odgovor leži.

Te celice se ustvarijo ali izberejo tako, da se v svojih točkah ponavljajočih enot nahajajo (sive točke slike). Glede na vrednosti parametrov, določenih v prejšnjem razdelku, konstantno za vsako enotno celico, je izpeljanih sedem kristalnih sistemov.

Vsak kristalni sistem ima svojo enotno celico; Drugi določa prvo. Na zgornji sliki je sedem polj, ki ustrezajo sedmim kristalnim sistemom; ali malo več povzetka, kristalne mreže. Tako na primer kubična enotna celica ustreza enemu od kristalnih sistemov, ki definira kubično kristalno omrežje.

Glede na sliko so kristalni sistemi ali omrežja:

-Kubični

-Tetragonalna

-OrtorRombica

-Šesterokotni

-Monoklinic

-Triklinična

-Trigonalni

Znotraj teh kristalnih sistemov pa drugi, ki sestavljajo štirinajst mrež Bravais; da so med vsemi kristalnimi omrežji najosnovnejši.

Kubični

V kocki so vse njene strani in koti enaki. Zato je v tej enotni celici izpolnjeno naslednje:

do = b = c

α = β = γ = 90 °

Obstajajo tri kubične enote celice: preproste ali primitivne, osredotočene na telo (BCC) in osredotočene na obraze (FCC). Razlike so v tem, kako se točke (atomi, ioni ali molekule) in v njih porazdelijo.

Katera od teh celic je najbolj kompaktna? Čigar glasnost je bolj zasedena s točkami: kubika je bila osredotočena na obraze. Upoštevajte, da če točke nadomestimo z mačkami in kozami na začetku, ne bi bili omejeni na eno celico; Pripadali bi in jih delili več. Spet bi bili to deli g ali c.

Lahko vam služi: hidrokoloid

Število enot

Če bi bile mačke ali koze v vrhovih, bi jih delile 8 enotnih celic; To pomeni, da bi vsaka celica imela 1/8 g ali c. Skupaj ali si predstavljajte 8 koc.

Če bi bile mačke ali koze na obrazu, bi jih delili le 2 enotni celici. Če ga želite videti, je dovolj, da zberemo dve kocki.

Po drugi strani pa bi, če bi bila mačka ali koza v središču kocke, pripadala le eni enotni celici; Enako se zgodi s polji glavne slike, ko je bil koncept obravnavan.

Rekel potem zgoraj, znotraj preproste kubične celice a Enota ali retikularna točka, saj ima 8 vrhov (1/8 x 8 = 1). Za kubično celico, osredotočeno na telo, imate: 8 vrhov, ki so enake atomu, in točko ali enoto v središču; Zato obstaja dva enote.

In za kubično celico, osredotočeno na obraze, imate: 8 vrhov (1) in šest obrazov, v katerih se deli polovica vsake točke ali enote (1/2 x 6 = 3); Zato ima štiri enote.

Tetragonalna

Podobne komentarje je mogoče narediti v zvezi z enotno celico za tetragonalni sistem. Njeni strukturni parametri so naslednji:

do = b ≠ c

α = β = γ = 90 °

OrtorRombica

Parametri za Ortorrombično celico so:

do ≠ b ≠ c

α = β = γ = 90 °

Monoklinic

Parametri za monoklinično celico so:

do ≠ b ≠ c

α = γ = 90 °; β ≠ 90 °

Triklinična

Parametri za triklinično celico so:

do ≠ b ≠ c

α ≠ β ≠ γ ≠ 90 °

Šesterokotni

Parametri za šestkotno celico so:

do = b ≠ c

α = β = 90 °; γ ≠ 120 °

Pravzaprav celica predstavlja tretji del šesterokotne prizme.

Trigonalni

In končno, parametri za trigonalno celico so:

do = b = c

α = β = γ ≠ 90 °

Reference

1. Whitten, Davis, Peck & Stanley. (2008). Kemija. (8. izd.). Cengage Learning P 474-477.
2. Shiver & Atkins. (2008). Anorganska kemija. (Četrta izdaja). MC Graw Hill.
3. Wikipedija. (2019). Primitivna celica. Pridobljeno iz: v.Wikipedija.org
4. Bryan Stephanie. (2019). Enotna celica: parametri latice in kubične strukture. Študij. Okrevano od: študij.com
5. Akademski center virov. (s.F.). Kristalne strukture. [PDF]. Illinois Institute of Technology. Pridobljeno iz: splet.iit.Edu
6. Belford Robert. (7. februar 2019). Kristalne latine in enotne celice. Kemija librettexts. Okrevano od: kem.Librettexts.org