Kapacitivne enote, formule, izračun, primeri

The Kapacitivnost Gre za razmerje med obremenitvijo kondenzatorja ali trenerja, merjeno v Coulombu, in njegovim električnim potencialom ali napetostjo, merjeno v voltih. Izraženo je v enotah Faradio (F) v čast Michaela Faradayja (1791-1867).

Kapacitivnost je opredeljena tudi kot lastnost ali zmogljivost kondenzatorja ali kompleta električnih kondenzatorjev, ki se meri s količino električnega naboja, ki ga je mogoče shraniti ločeno na enoto spremembe električnega potenciala.

Svetilke, pa tudi katera koli druga električna naprava, morajo biti del njihovega delovanja do kapacitivnosti. Vir: Pixabay.

Izraz kapacitivnost je uvedena kot posledica ustvarjanja električne naprave, imenovane kondenzator, ki jo je leta 1745 izumil pruski znanstvenik Ewald Georg von Kleist in neodvisno nizozemski fizik Pieter van Muschenbroek.

Kondenzatorji so električne naprave, ki shranijo električni naboj in ga takoj prenesejo. Ta lastnost je bila uporabljena v številnih električnih napravah, kot so televizija, radio, svetilke, računalnik, med drugim v vsakdanjem življenju.

[TOC]

Kondenzator in kapacitivnost

Kondenzator ali kondenzator sestavljata dva voznika, ki imata enake obremenitve in drugače. Vozniki se imenujejo oklepni oklep ali kondenzatorske plošče.

Plaka je povezana s pozitivnim (+) terminalom ene baterije, druga plošča pa je povezana z negativnim (-). Ker imajo plošče enake obremenitve in nasprotni znak, je neto obremenitev kondenzatorja nič (0).

Kapacitivnost je razmerje med obremenitvijo gonilnika ali prevodnikov, ki tvorijo kondenzator, in vrednostjo napetostne razlike med kondenzatorskimi ploščami.

Vam lahko postreže: Rosario hladilno sredstvo

Enote in formule

Formula kapacitivnosti je naslednja:

C = q / v

Kjer je C kapacitivnost, q obremenitev (katere enota je coulomb) in v  Napetost (volt)

Kapacitivna enota je Faradio (F), ki je enakovreden Coulomb / Voltio. Faradio je zelo velika enota, zato se uporablja mikrofradij (µF), kar ustreza 10^-6 farad; ali vrh Faradio (PF), ki je enakovreden 10^-12 farad.

Kako se izračuna kapacitivnost?

Kakšna bo vrednost kapacitivnosti kondenzatorja, katerega plošče imajo obremenitev 5 · 10^-3 Coulomb in 6 -voltna volponska razlika?

Uporaba formule, ki jo rešujemo:

C = q / v

= (5 · 10^-3 Coulomb) / (6 voltov)

= 8,33 · 10^-4  farad

Primeri

Formula kapacitivnosti se razlikuje glede na vrsto kondenzatorja.

Kondenzator vzporednih plošč

C = kε_tudiA / d

K je dielektrična konstanta, ki ima vrednost 1 v zraku in praznino. Zaradi tega se formula zmanjša na:

C = ε_tudiA / d

ε_tudi To je dielektrična konstanta, katere vrednost je blizu 8.854 · 10^-12 F · m^-1, A je območje ali površina vzporednih plošč, izraženih v m², medtem d Razdalja, ki ločuje vzporedne plošče.

Sferični kondenzator

C = 4πε_tudiR

Kjer je r polmer sfere v metrih.

Koncentrične sfere

C = 4πε_tudi / (1/ r₁ - 1/r₂)

Koncentrični kondenzator cilindra

C = 2πε_tudil/ln (r₂ / R₁)

Kje l je dolžina koncentričnih jeklenk v metrih.

Rešene vaje

Kondenzator vzporednih plošč

Kakšna bo zmogljivost kondenzatorja ali kondenzatorja v zraku s površino svojih 3 cm plošč² in ločen z razdaljo 2 mm?

Vam lahko služi: 12 primerov kemičnih baz

Imamo formulo:

C = ε_tudiA/d

In podatki:

ε_tudi = 8,854 x 10^-12 F · m^-1

A = 3 cm² (3 · 10^-4 m²)

D = 2 mm (2 · 10^-3 m)

Nadaljujte z zamenjavo:

C = (8,854 · 10^-12 F · m^-1) (3 · 10^-4 m²) / (2 · 10^-3 m)

= 1,3281 · 10^-14 F

Kondenzator ali sfera v obliki kondenzatorja

Če zemlja velja za sferični kondenzator s polmerom (r) 6.370 km: kakšna bo vrednost vaše kapacitivnosti?

Podatki:

C = 4πε_tudiR

Π = 3,1416

ε_tudi = 8,854 · 10^-12 F.m^-1

R = 6.370 km (6,37 · 10⁶ m)

Vrednosti v formuli kapacitivnosti se ponovno zamenjajo:

C = (4 · 3,1416) (8,854 · 10^-12 F · m^-1) (6,37 · 10⁶ m)

= 7,09 · 10^-8 F

= 709 µF

Kombinacija kondenzatorjev

Kondenzatorji ali kondenzatorji lahko kombinirate zaporedno ali vzporedno.

Kondenzatorji serije

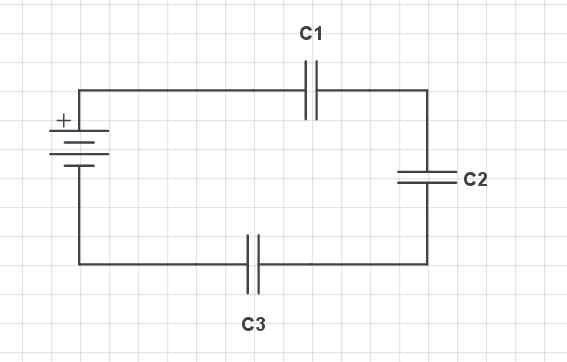Kondenzatorji serije. Vir Gabriel Bolívar prek CircuitLab

Zgornja slika prikazuje tri serije kondenzatorje (c₁, C₂ in c₃), pa tudi baterija s svojimi pozitivnimi (+) in negativnimi (-) terminali. Ti kondenzatorji imajo vrsto značilnosti glede na njihovo napetost, obremenitev in kapacitivnost.

Padec napetosti (ΔV) v kondenzatorjih

ΔV_t = ΔV₁   +   ΔV₂   +    ΔV₃

Skupni padec napetosti v nizu serijskih kondenzatorjev je enak vsoti napetosti padcev kondenzatorjev.

Breme  kondenzatorjev

Q_t = Q₁ = Q₂ = Q₃

Enaka količina obremenitve kroži skozi serijo.

Kapacitivnost kondenzatorjev

Enakovredna kapacitivnost serijskih kondenzatorjev predstavlja naslednje razmerje:

1 c_Eq  = 1/c₁  +   1 c₂   +   1 c₃

Vzporedni kondenzatorji

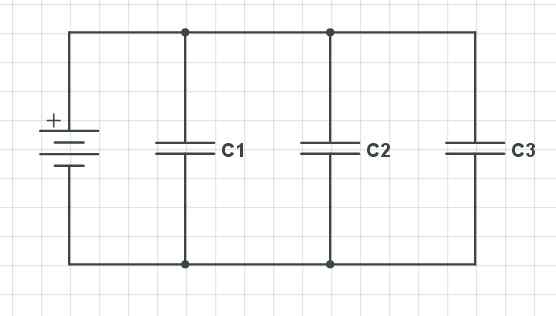Vzporedni kondenzatorji. Vir Gabriel Bolívar prek CircuitLab.

Zgoraj imamo tri kondenzatorje, razporejene vzporedno (c₁, C₂ in c₃), ki so glede na padec napetosti, obremenitev in kapacitivnost naslednje vedenje:

Vam lahko služi: alkeni

Padec napetosti v kondenzatorjih

ΔV_t  = ΔV₁  = ΔV₂  = ΔV₃

V vzporednih kondenzatorjih je skupni padec napetosti v kondenzatorjih enak obstoječemu za vsakega od kondenzatorjev.

Kondenzatorji

Q_t  = Q₁  +  Q₂  +  Q₃

V sistemu vzporedno je skupna obremenitev kondenzatorjev enaka vsoti obremenitve vseh kondenzatorjev.

Kapacitivnost kondenzatorjev

C_Eq  = C₁  +  C₂   +  C₃

V vzporednem sistemu je enakovredna kapacitivnost le -teh enaka vsoti kapacitivnosti vseh kondenzatorjev.

Primer vaje

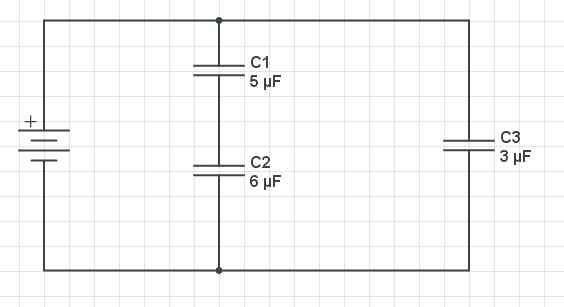Primer težave s težavami in vzporednimi kondenzatorji. Vir Gabriel Bolívar prek CircuitLab.

Zgoraj je prikazana shema treh kondenzatorjev: c₁ in c₂ So razporejeni v seriji in so vzporedno s C₃. Kapacitivnost kondenzatorjev je naslednja: c₁ = 5 µF, c₂ = 6 µF in c₃ = 3 µF. Poiščite enakovredno kapacitivnost vezja.

Najprej je enakovredna kapacitivnost C₁ in c₂ ki so v seriji.

1 c_EQ1,2 = 1/c₁  +  1 c₂

1 c_EQ1,2 = 1/5 µF +1/6 µF

1 c_EQ1,2 = (11/30) µf

C_EQ1,2 = 30 µF / 11

= 2,72 µF

Kondenzatorja 1 in 2 sta vzporedna s C₃. Torej, enakovredna kapacitivnost C₁, C₂ in c₃ je enak c_EQ1,2 +  C₃.

C_EQ1,2,3 = 2,72 µF +3 µF

= 5,72 µF

Reference

1. Serway, r. Do. in Jewett, J. W. (2009). Fizika za znanost in inženiring. Zvezek 2. Sedma izdaja. Uredništvo Cengage Learning.
2. Reddick, R in Halliday, D. (1965). Fizično.  2. del. Druga izdaja v španščini. Continental uredništvo s.Do.
3. Študij. (22. april 2015). Kapacitivnost: enote in formula. Okrevano od: študij.com
4. Lumes fizika. (s.F.). Kondenzatorji v seriji in vzporedno. Obnovi se od: tečajev.Lumenarning.com
5. Uredniki Enyclopeedia Britannica. (2020). Kapacitivnost. Okrevano od: Britannica.com